著名的数学家毕达哥拉斯曾说：“朋友是你灵魂的倩影，要像220与284一样亲密。”

就因为不经意的一句话，引发了一场数群和数学家长达几千年的“斗争”，甚至到现在依然没有结束！

今天，小编就扒一扒难缠的220和284——亲和数！

一天，他的门徒突发奇想问毕达哥拉斯：“我结交朋友时，会存在数的关系吗？”

随着门徒的一脸懵逼，亲和数就此横空出世！

亲和数问世之后，引起了一大波数学家对其进行研究。毕氏学派也趁着热度宣传讲学，不过宣传了几十年，讲到亲和数时，还是220和284。

直到毕达哥拉斯去世，也没能举出第二对亲和数的例子。

在之后的几百年里，数学界也没有再出现第二对亲和数，数学家都开始怀疑兴许毕达哥拉斯当时只是随口一说而已。

终于，皇天不负有心人，塔别脱·本·科拉研究出了亲和数的表达公式：

设 a=3*2^(x-1)-1, b=3*2^x-1,c=9*2^(2x-1)-1，这里x是大于1的自然数，如果a、b、c全是素数的话。那么2*x*ab与2*x*c。便是一对相亲和数。

例如，取x=2,得a=5,b=11,c=71,则2*2*5*11=220和2*2*71=284是一对亲和数。

公式一出，证明了毕达哥拉斯当年并没有瞎说，亲和数确实是存在，而且能通过公式去计算获得，事情开始变得有趣。

虽然塔别脱·本·科拉研究出了公式，但没能找到新的一对亲和数。毕竟要找到一对亲和数，需要大量的计算和出色的数感。

自那以后，数学家开始从寻找更简单方便的公式和在现有公式基础上计算寻找亲和数两个大方向攻克亲和数。

然而让人头疼的是，在之后的800多年，数学家们不但没有整出丁点关于亲和数公式的优化，甚至连一对新的亲和数都找不到！

直到1636年，我们的老朋友费马登场了，打破了两千多年的沉寂。

这位没有受过专业数学教育的“业余数学家”实在看不过眼了，白天打官司，晚上计算亲和数，通过大量的计算，甚至头发都花白了，终于找到了第二对亲和数：17296和18416。

一个律师居然做到了许多数学家做不到的事情！同一时代的数学家笛卡尔见状：不行啊，得给专业的数学家找回点面子。不惜放下将要成稿的《几何学》，立刻投身寻找亲和数。

然而，法国的两大数学家——闻名至今的数学大神费马和解析几何之父笛卡尔直到陨落，也没有找到关于亲和数更简便的公式和规律。

不过连续找到了两对亲和数，让数学家们重燃寻找亲和数的信心，许多数学家再次加入寻找亲和数的行列，他们企图用灵感与枯燥的计算发现新大陆。

可是在那之后的100多年里，并没有进一步的突破，无情的事实使他们省悟到，已经陷入了一座数学迷宫，不可能出现如法国人般的辉煌了。

正当大家被亲和数折磨得再次绝望的时候，欧大神从天而降，平地一声雷，大挫亲和数的锐气。

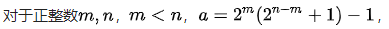
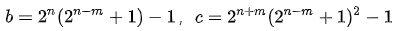
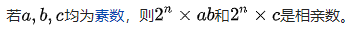
欧拉采用了新的方法，将亲和数划分为五种类型加以讨论。他超人的数学思维，解开了令人止步2500多年的难题，对于亲和数的研究达到了空前的高度，使数学家拍案叫绝。

原本以为亲和数就此画上句号，然而让人意外的是人称数学大神欧拉竟然也在亲和数上栽了跟头！

1867年，意大利有一个爱动脑筋，勤于计算的中学生——帕格尼尼，16岁他竟然发现了欧拉遗漏的一对亲和数1184和1210。

到了1923年，“吊打”过哥斯拉，费马，笛卡尔，欧拉等数学大神之后的亲和数，有点“飘了”。

后来，随着电子计算机的诞生，科学家们找到的亲和数越来越多。

如今，关于亲和数的研究却止步在了一个猜想上：若一对亲和数的数值越大，则这两个数之比越接近于1！

而这个猜想正在等着一位有缘人去掀开它的面纱，奋斗吧骚年，说不定下一个菲尔兹奖得主就是你！

马云曾说：数学是未来存活于世界的顶级能力！

记得要关注「超级数学建模」

0～99岁都可以关注的数学科普公众号

来源：超级数学建模

编辑：奶盖四季青