人类很早就知道用尺子画直线。可是，你能在没有尺子和绳子的情况下，也能画出直线，并且有百分百的自信自己画出的一定是直线吗？

直到150年前，人类对这个问题的答案是：不能。

正如证明了四色定理（如果在平面上划出一些邻接的有限区域，那么可以用四种颜色来给这些区域染色，使得每两个邻接区域染的颜色都不一样）的伦敦律师兼数学家阿尔弗雷德·布雷·肯普（A. B. Kempe）所说，你当然可以用直尺，甚至拉直的绳子画出一条看起来很直的线来，但问题在于，你怎么知道这条线足够直了呢？

伦敦律师兼数学家阿尔弗雷德·布雷·肯普（A. B. Kempe）

诚然，历史上有不少近似直线运动的机械被发明了出来，比如瓦特氏直线运动机构（1784年）。不过在150年前，没有任何工具在不借助导轨（如直尺）的情况下，能够画出完全笔直的线条。

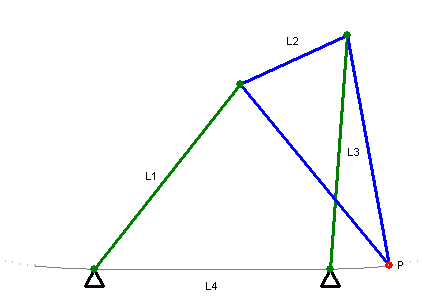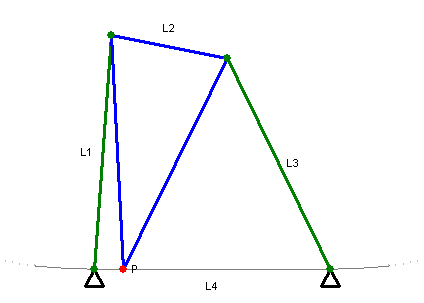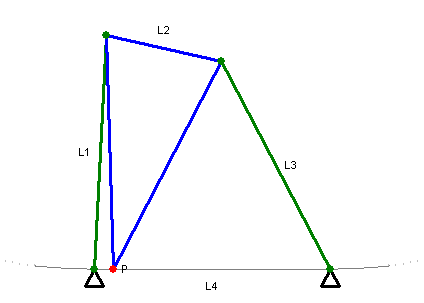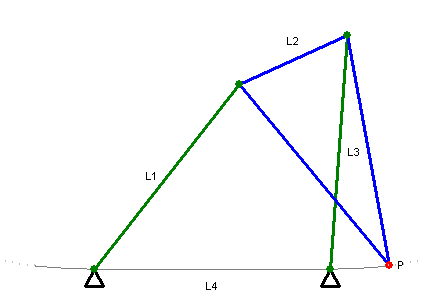
近似直线运动的连杆饶氏直线运动机构（Roberts Mechanism）

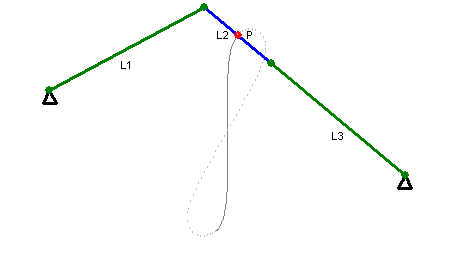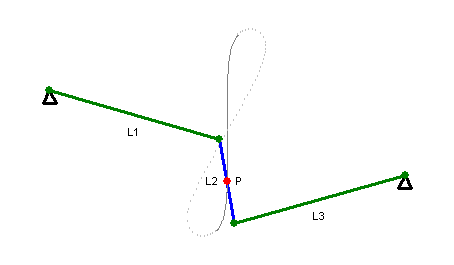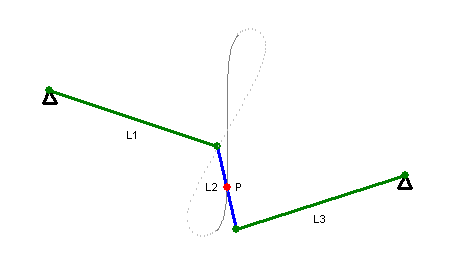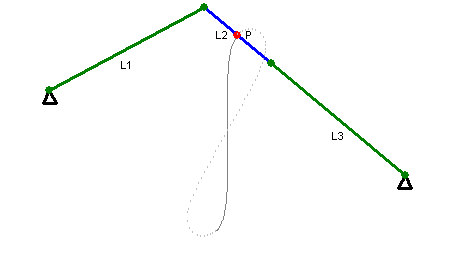
近似直线运动的瓦特氏直线运动机构（1784年）

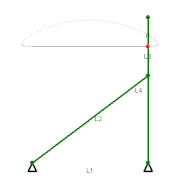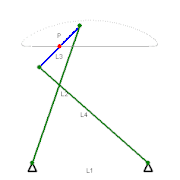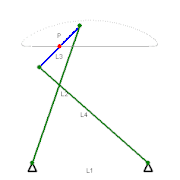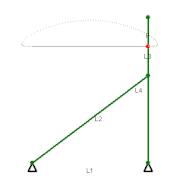
切比雪夫连杆机构

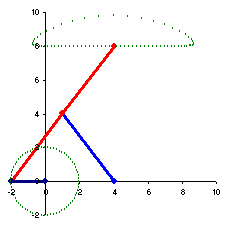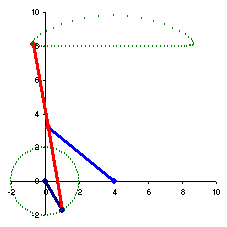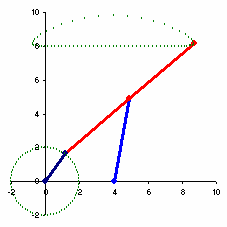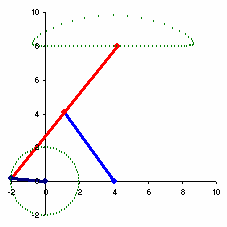
近似直线运动的切比雪夫λ连杆机构（1878年）

甚至有不少人试图证明能画出直线的连杆机构是不存在的，比如俄国著名数学家巴夫尼提·列波维奇·切比雪夫（Pafnutïĭ L'vovich Chebyshev）。

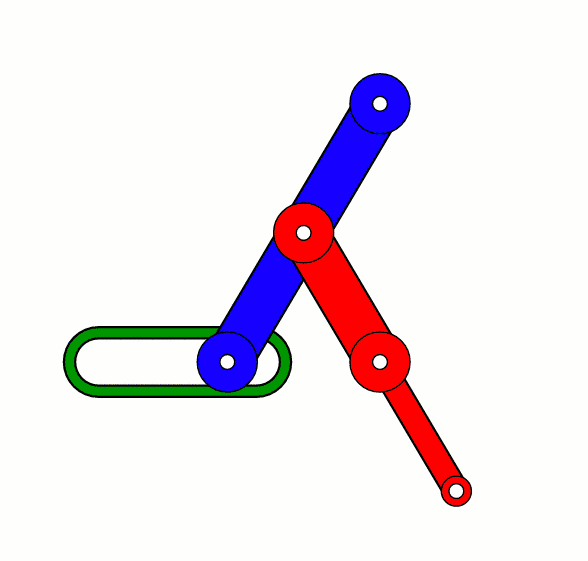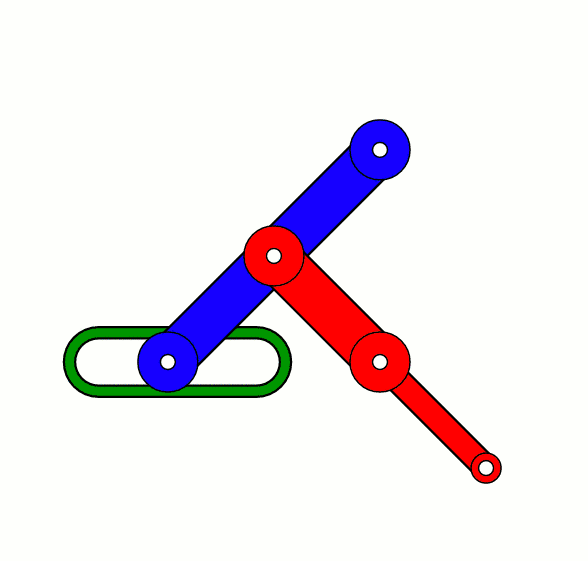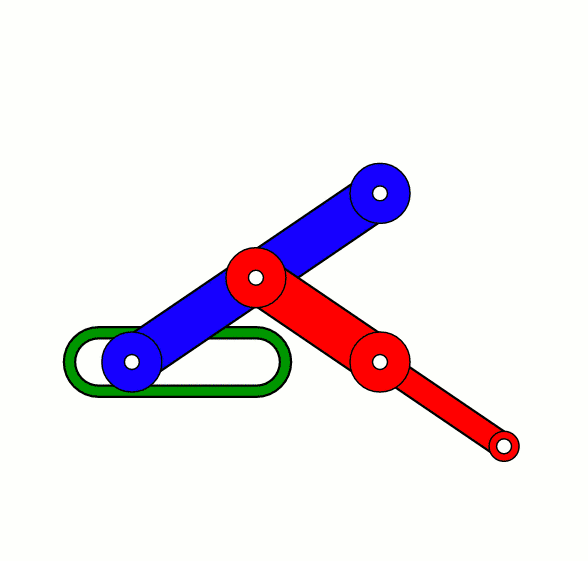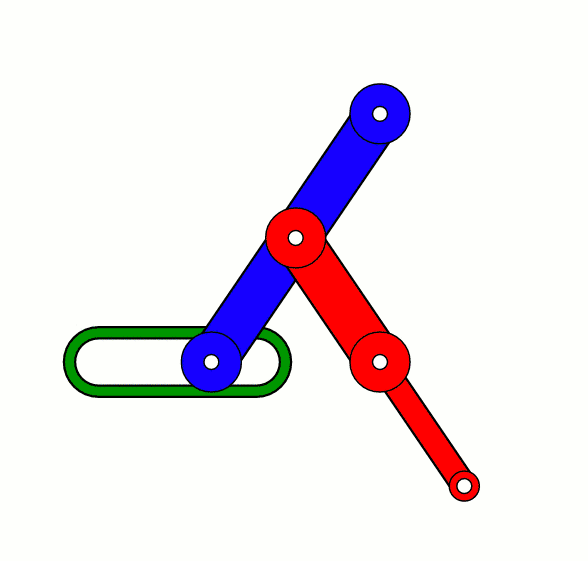
利用直线导轨运动的 Scott-Russel mechanism。在150年前，没有人，也

可是历史就会在意料不到的地方急转弯。1864年，一个叫做波氏连杆机构（Peaucellier-Lipkin mechanism）的直线平面连杆绘图工具横空出世。

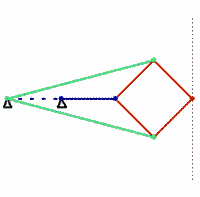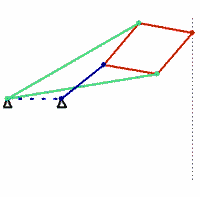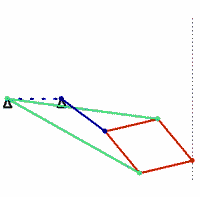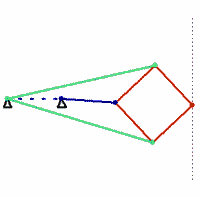
波氏连杆机构

波氏连杆机构是毕业于巴黎综合理工学院的法国海军军官 Charles-Nicolas Peaucellier (1832-1912)发明的。不过发明后的十几年里，波氏连杆机构并没有得到什么关注。到了1871年，俄罗斯圣彼得堡大学的一个学生Lipman Lipkin 也独立发明了这个有趣的直线运动机构，引起了轰动。

活塞头就需要波氏连杆机构。波氏连杆机构在蒸汽机的改良中也起到了重要作用。因为波氏连杆机构的出现，能够进行直线运动的机械臂也成为了可能。

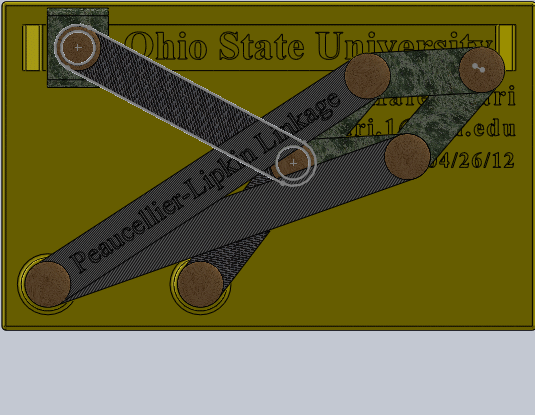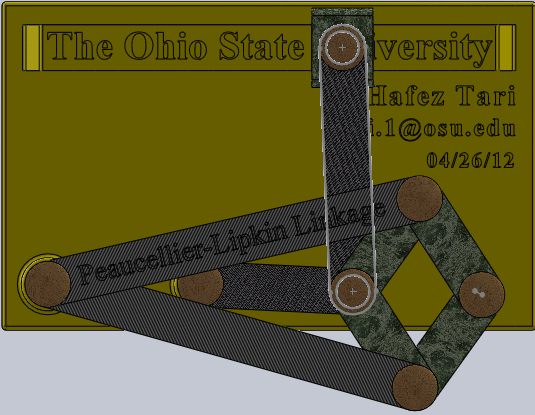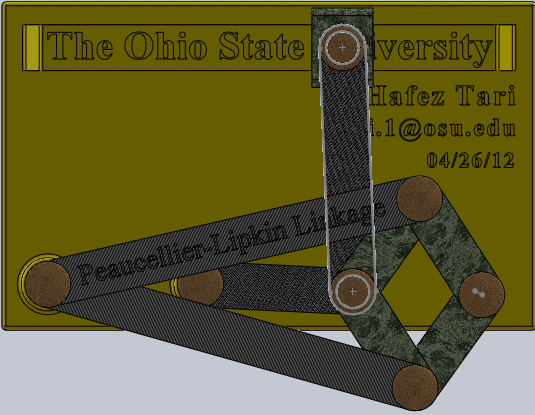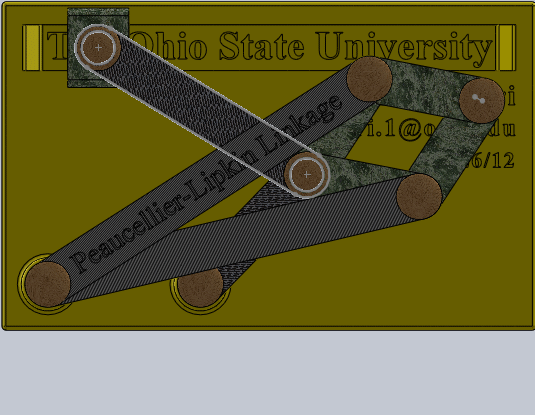
Lipman Lipkin 独立发明的波氏连杆机构

从数学上可以证明，波氏连杆机构能够画出完美的直线。肯普本人后来甚至还给出了一个定理：只要能用代数方程表示的平面曲线，都可以设计出一个连杆机构来实现。

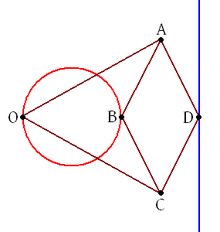
波氏连杆机构的几何原理：如果固定住O这个点，那么B和D互为反演；而又由于B在做圆周运动，根据圆的反演的性质（圆的反形是直线），D画出的图形是直线。

后来在1874年，Harry Hart 也发明了2款平面的直线连杆机构，动作非常妖娆。

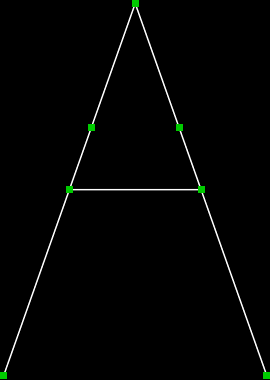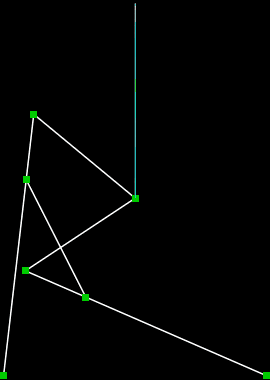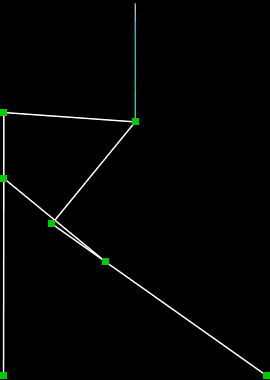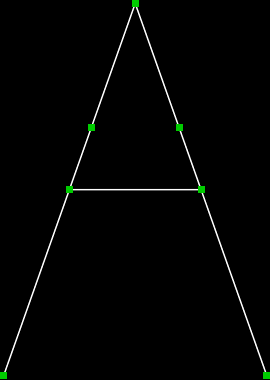
直线连杆机构 Hart's A-frame

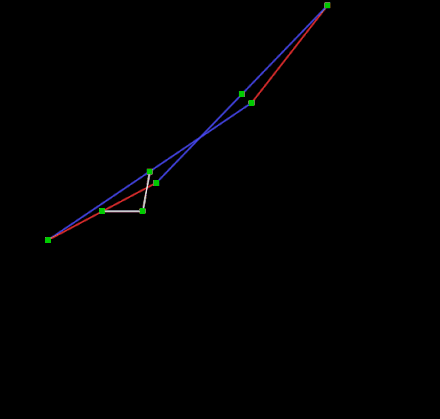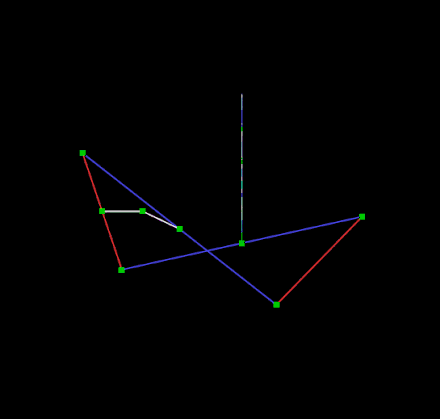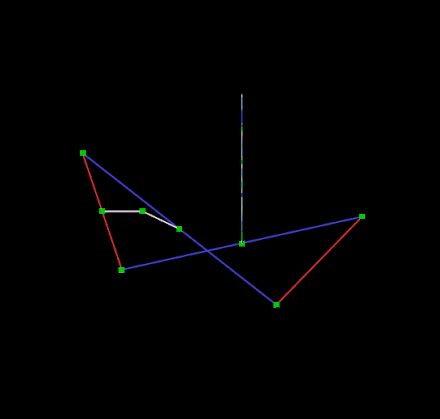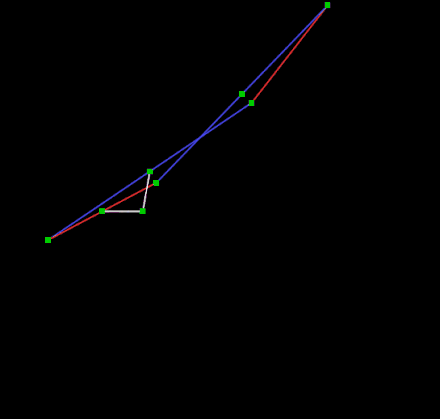
直线连杆机构 Hart's inversor

实际上，用三维的机构，也就是空间曲柄（space crank），也可以画出直线。其中一个有名的，就是萨鲁斯连杆机构（Sarrus linkage）。

它是在1853年被法国数学家 Pierre Frédéric Sarrus 发明的。不过人们花了很久才发现它的发明时间比波氏连杆机构早，因此还是有许多人认为波氏连杆机构是第一个能画出完美直线的机械。

不管谁是第一，能确定的是，就在150年前的短短几十年里，人类如开窍一般终于想出了一连串不用直尺画直线的方法。

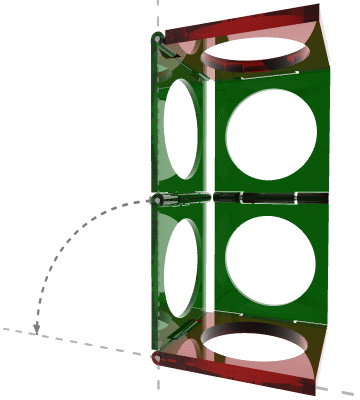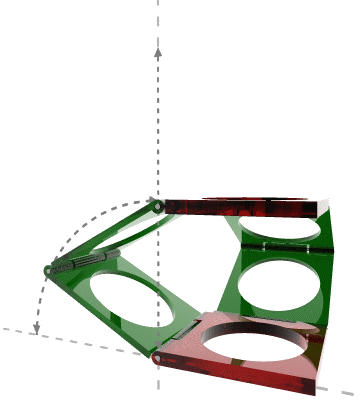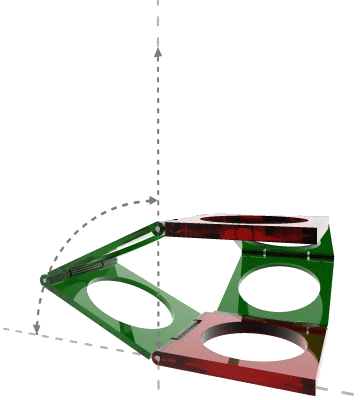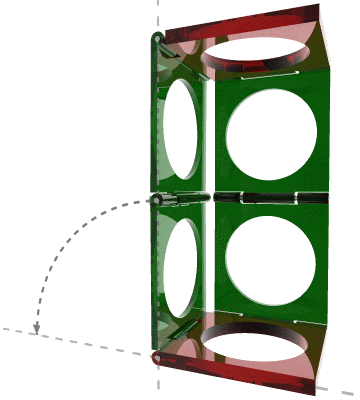
空间曲柄萨鲁斯连杆机构也能画出直线

萨鲁斯连杆机构变式

萨鲁斯连杆机构变式

萨鲁斯连杆机构变式

萨鲁斯连杆机构变式

看完本期内容我们明白，亚洲蹲就是萨鲁斯连杆，所以屁股能够着脚后跟。下次不喊报告，教官可能会让你做100个萨鲁斯连杆。