自习室 | 你的线性代数复习提纲正在向你跑来
线性代数是一门非常重要的基础课程,和高等数学一样,是理工科类学生学习其它课程的基础,一般线性代数这门课程会安排在大一第一学期,刚刚进入大学的大一新生往往对这门陌生的课程感到非常困惑,其实只要掌握好方法,再加上适当的练习,还是可以很简单学好线性代数这门课程的。
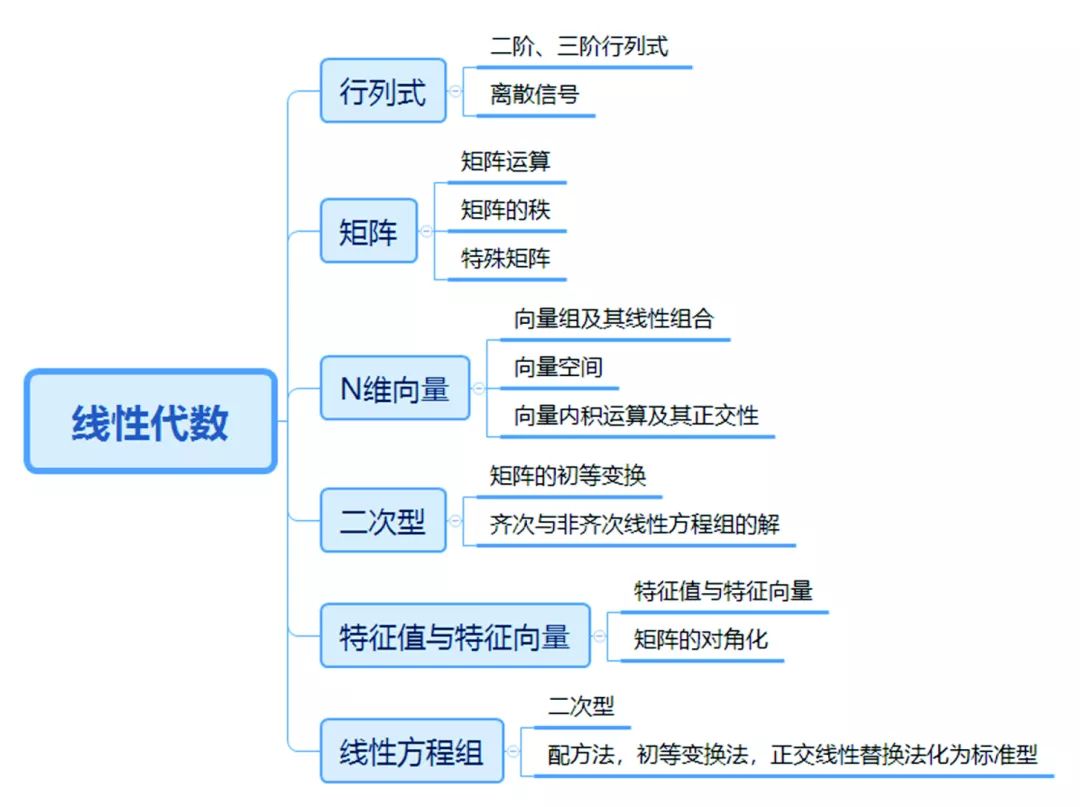
这里我将为大家介绍老师ppt上的经典教学顺序。一些重要概念已经加粗。
第一章
行列式(以计算为主线)
本章由二元、三元线性方程组引入二阶、三阶行列式,主要介绍行列式的概念、性质,重点讲解行列式的各种计算方法及技巧,最后给出行列式在解线性方程组中的应用——克莱姆法则.
第二章
矩阵(贯穿本书)
矩阵是线性代数中的重要内容,是研究向量组的线性相关性及线性方程组的解法的有力工具.本章首先介绍矩阵的概念及一些特殊矩阵,之后给出矩阵的运算,重点讲解矩阵的乘法运算,探讨矩阵的初等变换及其在矩阵运算中的应用.进一步研究矩阵的内在特性,包括可逆矩阵及矩阵的秩,最后给出分块矩阵及其运算.
第三章
n维向量(以讨论线性关系为主)
本章首先介绍n维向量的概念及向量的线性运算,之后讲解向量组及其线性组合,结合线性方程组和矩阵知识重点讨论向量组的线性相关性及向量组的秩,给出向量空间的概念及性质,最后介绍向量的内积运算及向量组的正交性.
第四章
线性方程组(以矩阵变换法为主)
本章首先由中学的二元、三元线性方程组引入解n元线性方程组的消元法,介绍如何利用矩阵的初等变换求解方程组,从而讨论线性方程组解的存在性,之后研究齐次和非齐次线性方程组解的结构,最后给出n元线性方程组的一般解.理解好这一章的其次以及非其次解对于后面学习信号与系统有非常大的帮助。
第五章
矩阵的特征值与特征向量(以方阵对角化为主)
本章首先介绍矩阵的特征值与特征向量的概念及求解方法,之后引入相似矩阵,重点研究矩阵的对角化问题,特别是实对称矩阵的对角化.
第六章
二次型(以化标准形为主)
本章首先介绍二次型及其矩阵表示,重点讲解化二次型为标准形的三种方法——配方法、初等变换法和正交线性替换法,最后给出正定二次型的概念及判定方法.这一章的内容非常重要,一定要在理解的基础上掌握。
学习线性代数掌握方法最重要,有人非常努力的学习线性代数,也做了非常多的题目,但是因为没有掌握正确的方法,取得的成绩总是不尽人意。在我看来,线性代数和高等数学的学习有不同的地方,高等数学需要记住非常多的公式和大量的练习,而线性代数最重要的在于思考,只要思路正确,就会大大的简化计算,从而轻松地解出题目。
祝愿大家在接下来的考试里取得好成绩~

供稿:信息科学与技术学院学业发展中心
本期作者:夏嘉伟 刘衬清 刘艳玲
编辑:周洪浩

西南交通大学信息科学与技术学院in传媒
inmedia@home.swjtu.edu.cn




