下面对建模过程中由于不同单元选择，可能出现的问题进行一下总结。

01. 沙漏现象：

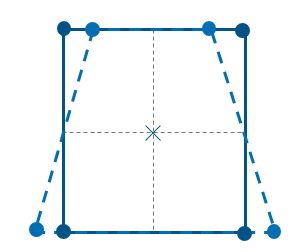
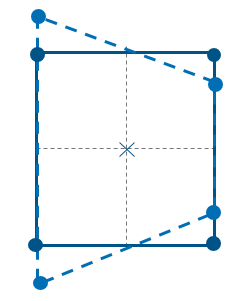
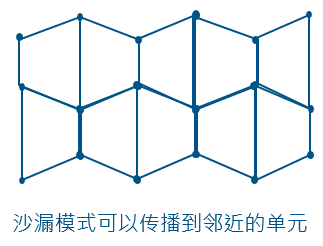
对于一阶缩减积分四边形与六面体单元，其沙漏模式可以传播。

Abaqus提供了沙漏控制的方法：

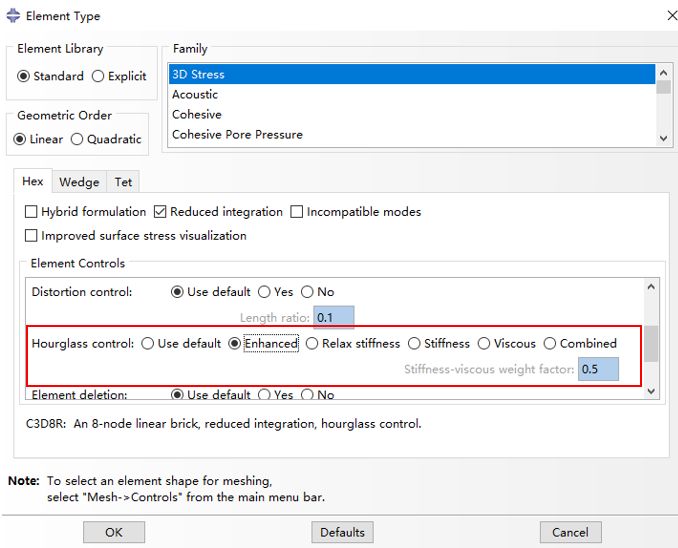
对于弹性弯曲以及粗网格的情况，采用增强沙漏控制的方法能够计算得到相对高精度的结果；

对于塑性弯曲问题， 采用基于刚度的沙漏控制可以得到比较好的计算结果。

对于弯曲问题，在厚度方向上通过增加单元层数，可以有效的提高计算结果精度。

在使用沙漏控制的模型中，要确保计算结果中伪能量相对于总内能比值控制在（<1%）范围内：

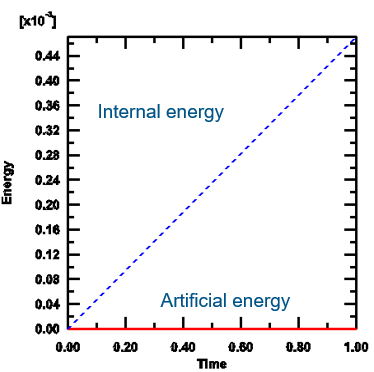
02. 不可压缩材料（体积锁定）：

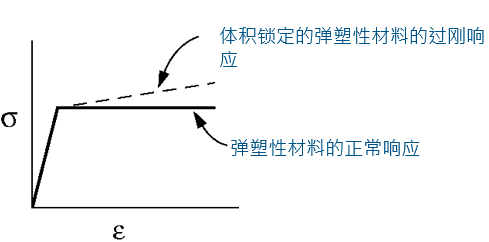
许多非线性问题涉及不可压缩材料(泊松比 v=0.5)以及几乎不可压缩的材料(泊松比 v>0.475)。

传统的有限元网格往往由于体积锁定而表现出过度的刚性行为，当材料受到高度约束时，这种情况最为严重。

对于采用该类材料的模型，可以通过使用以下方法处理：

缩减积分单元（C3D*R）；

杂交单元 （C3D*H）；

改进的表面应力可视化四面体单元（C3D8S）;

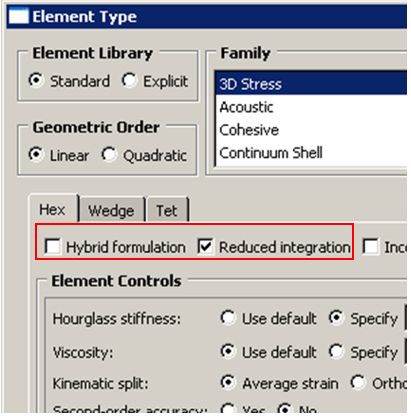
03. 弯曲与剪切锁定：

对于二阶全积分与缩减积分单元，均可以很好的模拟弯曲问题。

对于采用一阶全积分实体单元进行弯曲建模，可以看到在积分点位置能够检测到剪切应变，实际上结构中不存在剪切应变。这种行为导致能量转化为单元剪切势能而非单元弯曲势能，以上情况会造成单元剪切锁定现象。

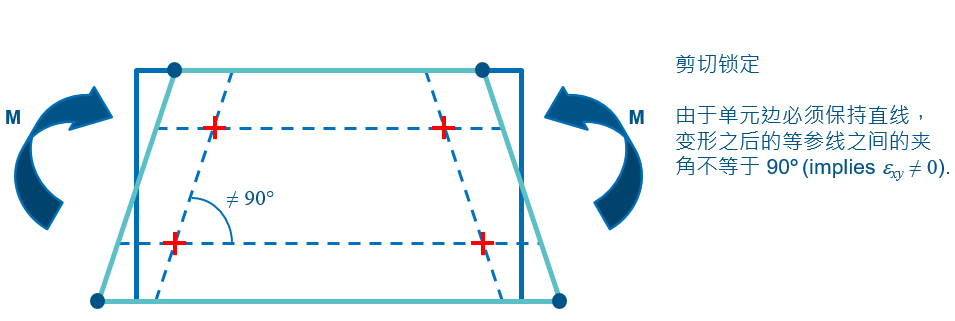
为了使用一阶单元也可以进行弯曲建模，可以通过采用缩减积分单元，同时在弯曲厚度方向上定义大于四层单元的方法实现。

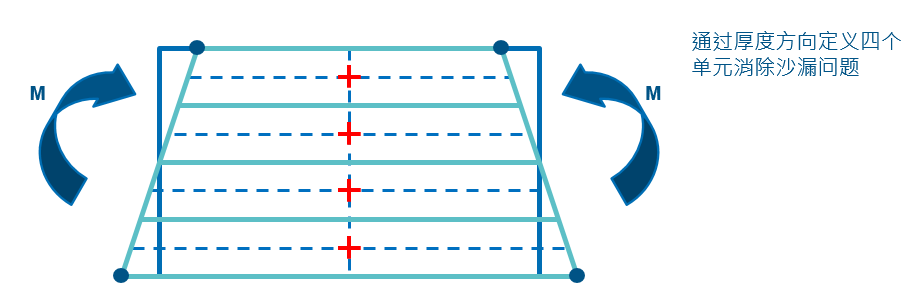
除此之外，采用非协调单元（C3D*I）也可以有效的消除寄生剪应力，获得精确的弯曲工况计算结果。

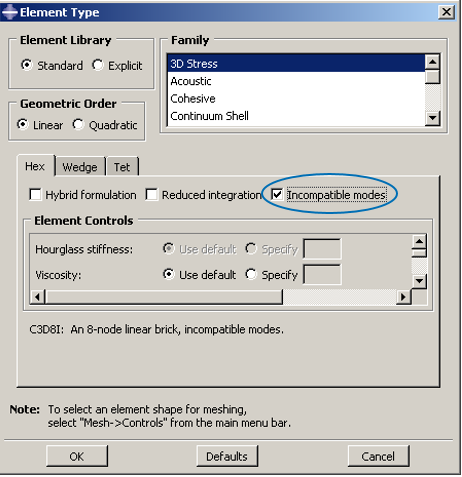
04. 应力集中问题：

在应力集中的问题中，二阶单元明显优于一阶单元，非常适合于分析(稳态)裂纹。二阶完全积分和缩减积分单元都可以很好地工作。缩减积分单元往往更有效——结果通常与完全积分单元一样好或更好，并且计算成本更低。

05. 二阶精度控制：

对于存在多周旋转的情况，特别是当旋转机构的转动圈数大于5圈的情况下，采用二阶精度控制能够得到较高的计算精度。

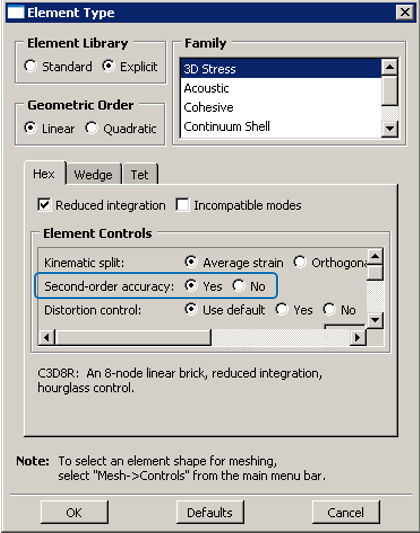
旋转5圈之后一阶精度控制出现不稳定的情况

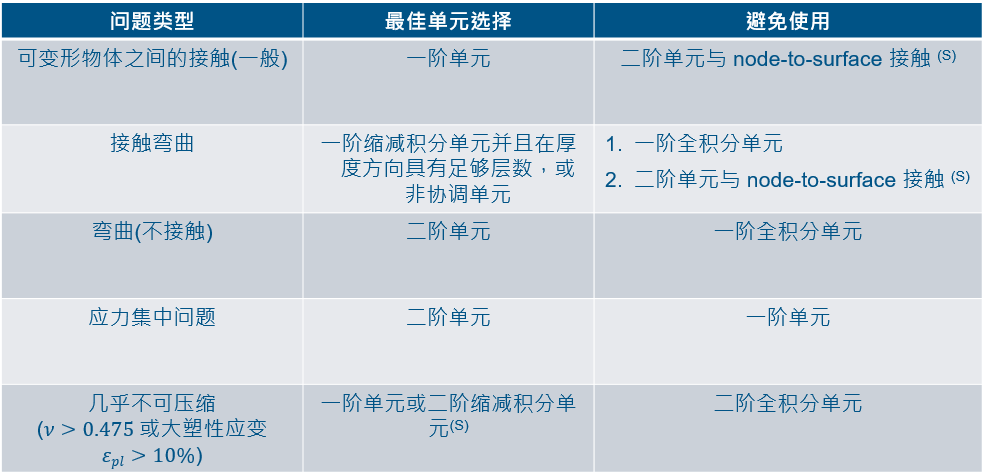
06. 对应工况单元选择列表：

对于应对不同情况的单元选择， 提供以下列表，方便用户进行选择：

\ CAE工程师精品课 \

仅售 ¥9.9 | 淘口令 $haqk1XWSTfi$

仅售 ¥35 | 淘口令 ₳FBZ51XWSWHX₳