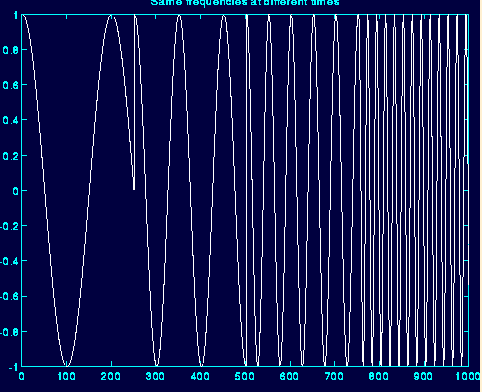
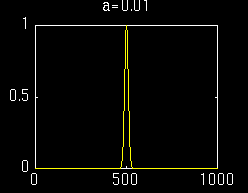
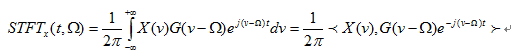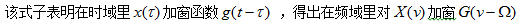傅里叶变换的本质及其公式解析
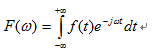
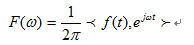
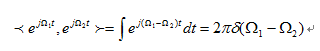
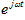
求内积的时候,只有f(t)中频率为

才会有内积的结果,其余分量的内积为0。可以理解为f(t)在
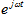
上的投影,积分值是时间从负无穷到正无穷的积分,就是把信号每个时间在
 叠加起来,可以理解为f(t)在
叠加起来,可以理解为f(t)在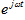
上的投影的叠加,叠加的结果就是频率为
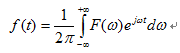
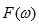 和
和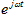 求内积的时候,
求内积的时候,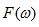 只有t时刻的分量内积才会有结果,其余时间分量内积结果为0,同样积分值是频率从负无穷到正无穷的积分,就是把信号在每个频率在t时刻上的分量叠加起来,叠加的结果就是f(t)在t时刻的值,这就回到了我们观察信号最初的时域。
只有t时刻的分量内积才会有结果,其余时间分量内积结果为0,同样积分值是频率从负无穷到正无穷的积分,就是把信号在每个频率在t时刻上的分量叠加起来,叠加的结果就是f(t)在t时刻的值,这就回到了我们观察信号最初的时域。
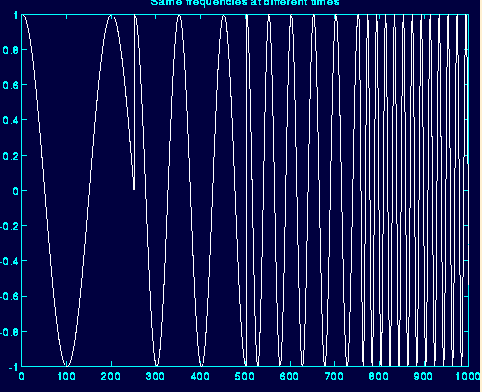
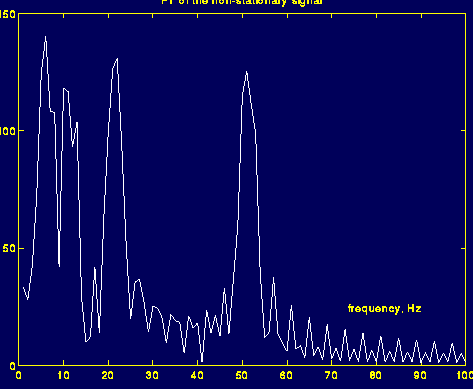
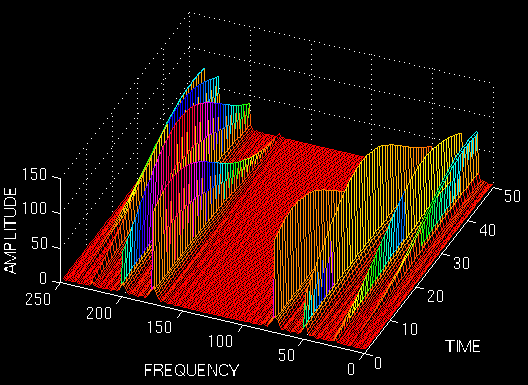
短时傅里叶变换
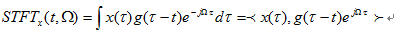
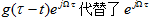 ,实现了局部信号的频谱分析。
,实现了局部信号的频谱分析。