曹则贤:狭义相对论初步 【云里·悟理-第3课】

第三课
狭义相对论初步
主讲人

大家好,欢迎来到《云里·悟理》系列课程,这里是中国科学院物理研究所,我是曹则贤。
我们今天来聊一个近代物理里面一个比较难、但是也是非常有趣的一个话题,就是相对论。大家可能都听说过相对论,而且提起相对论,很多人会想起一个关键人物——就是(他其实是)德国人,但是是在瑞士接受的高等教育和在瑞士工作的一个人,叫阿尔伯特·爱因斯坦。但是我们大家也不要误解——相对论不是爱因斯坦唯一的成就,也不是爱因斯坦一个人的成就。实际上相对论的思想应该说,作为物理学的一个思想,它源远流长。如果我们愿意从意大利人伽利略那个时候算起的话,那么到爱因斯坦创立狭义相对论的时候也已经是300多年了,那么可以说物理学的思想是一条非常绵密的河流。那么在这样的一个绵密的历史长河中,许多人为(这)一个伟大的物理思想都做出了自己的贡献。相对论的关键思想就是变换不变性,也就是平常我们所说的:要学会从不变中去把握变化。那么相对论应该说,对于我们每一个学物理的人来说,可能都是比较难的一个课题。
因此我提醒各位中学生朋友们,不要试图因为一下听不懂就不听了。因为你不能指望上来就学得懂,但是你要坚持“听说过”,你要让听得怎么说,心里有一种痒痒的感觉,让你愿意花时间去学下去,将来有一天你一定能够学会的。
物理理论是如何建立的
在聊相对论之前,我觉得我们首先要问一个问题,就是物理学到底是干什么的。可以说我们的物理学是为了认识这个宇宙,找出宇宙中一切过程的规律,并且在认识宇宙的这基础上,我们还要做一些创造。那么现在我们回到第一条——就是如何去认识宇宙、如何去描述这个宇宙中发生的各种事件。那么这就引出了我们物理学的一个“第零定律”。这个“第零定律”强调的什么呢?就是我们这个宇宙,如果你作为一个大舞台的话,你怎么去从几何的角度去描述它。那么我们物理学的“第零定律”认为,我们的宇宙是一个三维的空间,就是大家习惯的上下前后左右,另外还有时间,因此我们描述宇宙这个大舞台所用的参数就是三个空间的参数,加上一个时间的参数——所谓的x、y、z加上t。但是将来,大家如果对相对论了解多的话,那么就会发现:我们后边t所谓的时间本身不是一件容易的事情。
比方说我们在狭义相对论里面,会把它表示成ict的形式。那个i 有些同学可能听说过叫虚数,而那个c就是光速。那么从这个时候,大家可能就会觉得了,时间不是一个简单的问题。这一关于时间的问题,等大家将来学了足够多的物理的时候再去深入思考它。在这里面我们假设大家知道什么叫时间,时间就是你拿起你的手表或者你的手机所记录那些时间就好了。那么构造物理学的理论有什么方法呢?
第一种方法就是平常所说的构建法——就是我们先通过观察这个宇宙,然后找出一些事实,找出它中间的关联,再提取出里面的理论。这个大家可能比较熟悉的。比方说我们的力学啊,研究电磁现象啊,都是这样的方法。比方说关于单摆——就是伽利略看这个风中摇摆的这个吊灯,它的这一个周期和底下摆锤的重量无关;以及摆锤的长度越长,摆绳的长度越长,周期越长。于是乎总结出了单摆的周期的平方和摆绳长度成正比这样一个规律。

伽利略观察吊灯
另外一个就是人们观察落体,比方说屋檐下水滴的下落。如果我们大家仔细观察的话,就会发现越往下两滴水滴之间距离越大。所以说我们提取出一个概念:原来地球表面上下落的过程是个加速的过程。可是加速又是怎么个加速法呢?然后我们就会发现雨滴或者从天上掉下一块小石头,它往下到达地面速度的平方和下落的高度成正比的。那么如果我们把速度平方的改变和下落高度的改变成正比这个事情给表达清楚的话,我们就会表达出刚才我们这个PPT上的这样一个性质——就是说一个是质量m乘上g,乘上它的高度差H1-H2,就和等于质量乘上它的速度平方的差。那么移项以后,我们就会得出一个表达式,大家看就是:mgH1+1/2mv²=mgH2+1/2mv2²。那么注意这个方程,实际上是个非常重要的方程——因为它左边只和下标1有关系,而右边只和下标2有关系。而如果一个方程,它的左侧只和某一个事物有关系,右边只和另外一个和它同样的事物有关系,那说明我们这个方程的这样一个表达和谁都没有关系。因此我们就得出了一个很重要的一个结论:就是一滴雨滴或者一个小石子,在下落过程中,它所处的高度以及和它当时的速度一个恰当的组合就是mgH加上1/2mv²。这样的一个东西是一个常数,这就是所谓的机械能守恒定律。
那么对于这样的一个定律的发现,实际上有很多人做出伟大的贡献。比方说有约翰·伯努利;但是还有一个很重要的一位女科学家,就是沙特莱侯爵夫人。

沙特莱侯爵夫人
那么另外一个研究物理的方式,我们管它叫原理性的方法。什么意思呢?就是我们从一个道理出发,然后从这个道理出发去要求我们的物理的理论该具有样子。比方说你们将来上大学的时候,会学一门课,关于冷热的科学,这个就叫热力学。而热力学就是一门原理性的学科,它是从一个基本的原理出发。什么样的原理呢?就是一个法国人叫卡诺的总结出那个“热机该怎么工作的”一个重要原理。他这个原理就是简单的一句话,叫“凡事不以干活为目的的传热都是浪费”。那么从这样的一个原则出发,我们就知道,一个最好的、效率最高的热机,它的工作过程就是我们这图里那一个不规则四边形所表示的过程。就是有两个绝热过程,加上两个等温过程组成的。那么有了这样的一个基本的过程——这就是我们研究热力学的出发点。那么从这个图里面,我们就能总结出热力学第一定律:所谓的Q1-Q2=W。还有热力学的第二定律,就是Q1/T1-Q2/T2=0。那么能够总结出这样的一个,热力学第二定律,能够写出它的微分的形式,那么一个德国人鲁道夫·克劳修斯就总结出了熵。然后接下来就会有热力学的很多很多的内容。
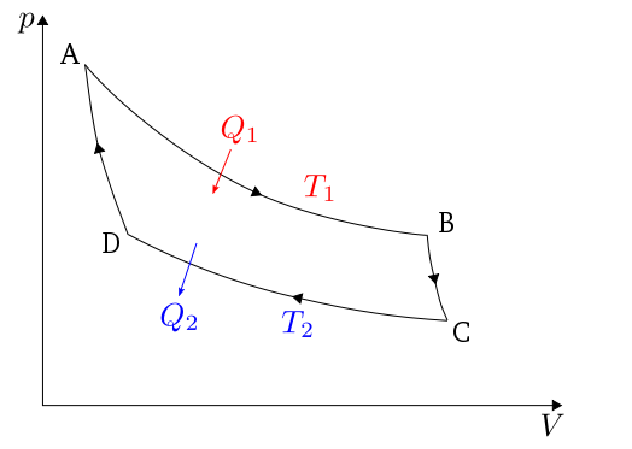

卡诺
那么这些内容大家可能不懂,但是请大家记住这是一个非常有效的构造物理学理论的方法。就是从一个原理的出发,而这个原理也是大家非常容易能够理解的一个简单一句话:凡是不以干活为目的的传热过程都是浪费。那么如果我们非要说同学们一个学习过程的话,我也可以提醒大家:凡是不以获取知识本身为目的的学习都是浪费。
相对论的思想源流
那么与热力学相比相类似的,就是我们的相对论。我们的相对论也是一个原理性的学问。相对论我们说的就是一个相对性原理,那么这个相对性原理,如果仅仅是表达成,这个说它的原理的话,其实比较简单。它说的是什么呢?物理学的规律和你描述这个规律的你所处的运动状态、物理学家所处于运动状态、你在哪个位置、是用什么速度运动、你有什么加速度,没有关系。而且对于这个理论,还因此也提出一个非常重要的要求,就是你写出来的物理规律的表达式和你所用的你所处在什么参考系、你所使用的什么坐标系,是没关系的。大家看这个原理很简单,就是说和物理学家和你观察者无关,写出的方程样子要一模一样。这看似是一个非常简单的一个要求,其实我们会注意到,它对数学的要求是非常非常高的。举例来说,我们站在一个运动的平板上面,我们释放一颗苹果,那么这个苹果下落的过程,对于站在平板上的人来说,它是一个垂直下落的轨迹;那么对于站在地面上的人,他看到苹果下落的轨迹,是一条抛物线。也就是说大家站在不同的,处于不同的状态,观察到苹果的运动轨迹是不一样子的。但是我们由此总结出来的力学规律是一样子的——就是说苹果,它自由下落的过程,它的加速度就应该是重力加速度,这个表达式应该是一样子的。
当然这只是最简单的一个例子,相对论要比这个复杂一点。那么相对论,我们从哪儿开始聊?就是第一条我们要记住的,就是说这个世界的规律和我们所处的“观点”——“观点”就是你看问题你站在那个地方这个“观点”——和“观点”无关。那么一个简单的例子呢,就是我们物理学史上,我们看我们的邻居、火星的轨道。那么火星在我们地球上面,你看到它这个运行轨迹是一团乱麻似的。但是如果我们能够把我们的“观点”挪到太阳上面,你会发现:火星的轨道和我们地球的轨道是几乎一样的,都差不多是个圆形、或者稍微有一点点扁的这样一个椭圆。那么这个就告诉我们:不管我们看到的这个一团乱麻,是从我们视角下面看到的火星像乱麻一样的轨道、还是从太阳的角度看到的火星是一个椭圆的轨道,那么这里面这个底下的物理的规律是一样的。也就是说我们太阳系的行星,是受太阳的吸引。这个吸引力是牛顿(万有)引力,是平方反比律。那么对于这样的地球和火星,我们的轨道是以太阳为焦点之一的椭圆,那么这个规律是不变的。
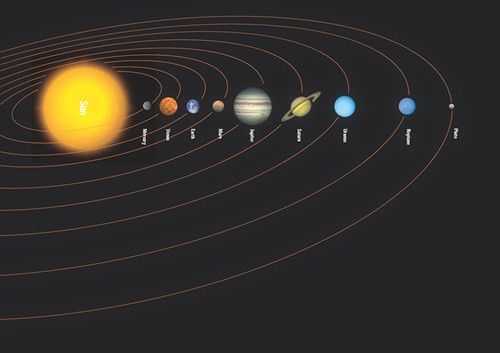
物理规律和参照点选择无关
那么相对论接下来就又往下进一步,这是我们的老祖宗早就注意到的。然后在差不多17世纪初,意大利人伽利略描述的一个非常重要的现象——就是当我们处在一个船舱里面,而船在匀速运动的时候,我们是感觉不到这个船的运动的。那么这样的一个思想,现在我们管它叫“伽利略相对论”。说的什么意思呢?说的是,如果你站在一个匀速运动的平台上,和一个相对静止的这样的一个平台上观察同一个物理现象的话,你得到的关于现象的描述、以及得到的物理学的规律,和你们两者之间的相对的速度是无关的。那么这样的刚才我们提到的就是,仅仅是改动“观点”、以及两个观察者有不同的速度差别,你看到应该看到同样的物理规律和这样的思想。其实我们老祖宗早就总结出了这样的一个智慧。在北京西山的大觉寺有这样的两块匾额,一个上面的四个字叫“无去来处”,另一个上面是四个字叫“动静等观”。这非常明晰地就说出了这两种思想。当然了我们最重要的是,作为物理学家,要学会把这样的思想用公式表达出来。下面就是那两个公式,我就不给大家细讲了,希望大家以后有机会都能多学这一点。


那么接下来我们大家要注意到,就是说在我们谈论相对运动的时候——就是你们可能小学的时候就做了许多算术题——那么你注意到它的表达是什么样子呢?都是这样说,什么水流相对于岸的速度是多少、船相对于水流的速度是多少?然后求这个船相对岸的速度,或者说火车相对于大地的速度是v1,然后你在车厢里面相对车厢走路的速度是v2,求你相对于大地的速度v。然后老师都会教你这个速度等于多少,说v=v1+v2。那么这里面重要的一点是什么?请大家记住那个相对那个词,就是当我们日常在谈论速度这个概念的时候,我们总是提起来有参照物,是相对于什么什么的速度。那么这个思想好像一直是对的,但直到有一天我们发现有一个新的问题了。那么这个问题是什么呢?这个问题就是关于电磁的现象,那么电磁的现象到了1860~1864年这一段时间里面,英国有一个著名的物理学家叫麦克斯韦。麦克斯韦就把这些描述电磁现象的这四个方程——我们现在管它叫“麦克斯韦方程组”——又改写成了什么呢?改写成了这样的一个叫麦克斯韦波动方程的形式。而这个波动方程,和我们从前的力学里面描述一根琴弦怎么振动的这样一根方程,就是琴弦的方程,竟然长得是一模一样子的。我们知道琴弦的振动发出什么呢?发出声音声波。那么我们自然就会猜想,难道我这个电磁过程,也会往外发射出波吗?那么这才是关于电磁波的猜想。那么这个猜想出来十来年,刚到了1887年的时候,德国人、一个叫赫兹的人就用了这套,这个电感电容组成的线路,证明了确实是有电磁波。

麦克斯韦
好,既然真的有电磁波,我们就应该拿着麦克斯韦总结出的,这个麦克斯韦波动方程当真了。那么我们看一个波,我们知道波有速度。那么波的速度在哪里呢?就在方程里面。大家看到方程里有个
μ0ε0,那个东西你把它开平方就能够得出光速了。那么用μ0ε0计算一下这一个所谓电磁波的速度呢,发现竟然和当时测到的光速差不多。这个就引导人们去想:难道我们的光,我们很熟悉的光,真的就是电磁波吗?那么好,我们注意到了光确实是电磁波,但是接下来的问题就来了。就是光的速度是相对于谁的速度?我们以前谈什么船的速度啊、火车的速度啊,我们都始终会明确的指出它的参照物是谁——船相对与岸啊、火车相对于大地啊。但是这地方麻烦了;因为我这个速度本身是从两个常数μ0ε0计算来的,我这地方根本就没有参照物这件事情。
那么这个地方就会引导人们认识到一个非常不太容易,一下子转过弯的这样的一个结论,就是光它的速度是没有参照物的,相对于谁它都是这个值 。这一个观念是我们学相对论要特别特别注意的一个观念,不是光速变不变,而是光速没有参照物。那么,这一个电磁学的过程,就是认识到——有电磁波给我们带来一个非常重要的挑战——就是我们怎么能够描述这样的现象,使得它不管是在我们运动的,这样的一个参照框架里也好,还是我们静止的参照框架里也好,我们看到的物理现象它的规律是一样子的。那么这个就要求,许多人从数学的角度来努力。比方说我们从一个点,比方说就是蜡烛头吧,我们往外发出光,那么我们如果是相对蜡烛静止呢,我们知道从蜡烛头这地方发出的光是均匀的四散开来的,那么这个光应该是球面波,一直是往外扩散像个球。那么你怎么能够用一个数学的方式说服我?就是如果你运动起来,然后你在你运动的框架里面,你描述这个蜡烛头发出光,你给我说你看到的,也是从蜡烛头那个地方,以它为球心均匀的往外发出了球形波。
你怎么能做到这一点?那么这个就是关于麦克斯韦波动方程或者说是三维空间加一维时间,这个距离的公式就是dx²+dy²+dz²-c²dt²,就是说你怎么能够让它在你运动的时候和你静止的时候你看到的距离都一样子的,或者说你看到了一个发出球面波的过程,永远都是一个发出球面波的过程。那么这样的一个数学是德国人福格特(在)1887年,后来荷兰人洛伦兹在1904年给我们得出了这样的一个表达式,就是左边这样一套x' y' z' t'和另外一个参照系里面的xyz和t之间的关系,这个数学表达式是我们学狭义相对论,必须要记住的一个表达式,这个表达式就叫洛伦兹变换。
所以大家记住关于狭义相对论,现在有两个重要的概念了:一、光速没有参照系,它就是一个常数;二、就是不同运动状态下不同速度下你看到那个事件,你用到的这样一个时间和空间的坐标之间的变化或者变换就是这样的一个式子,这个叫洛伦兹变换。所以说洛伦兹变换和光速没有参照系,这两条是我们学习狭义相对论要记住的两点。
那么有了这样的一个思想和有这样一个洛伦兹变换的表达,你会发现它很快的就会给我们带出非常非常重要的物理。比方说我们觉得我们在一个静止的参照系里面描述世界,然后我用一个速度v1运动起来,我们又得到了这个时间和空间的变换。但是如果有人在相对于运动的我,又用一个速度v2,那么它就既有相对于我的一个变换,又有相对于完全不动的状态,那个参照系的一个变换那么这个变换之间的关系,就能得出所谓的你们在狭义相对论的科普书里能看到这个很重要的速度相加的公式——就是这里面的(v1+v2)/(1+v1v2/c²)这样一个公式。那么许多的书里会说,你看这个公式里面,如果v1、v2都是≤c的话,那么加出来的速度v也永远≤c,有些人就把它理解为所谓的光速不变,不对的。这个地方正确的理解是说我们的有质量的物体运动的速度,就是说你的上限你永远能够渴望,但是其实你永远达不到的上限是光的速度。应该这么理解,那么这样一个表达式(v1+v2)/(1+v1v2/c²),这样的表达式有时候记起来可能不好记,那么我告诉大家,这个公式其实就是你们在初二的时候学过的tan(θ1+θ2) 的展开式。至于这个细节希望大家以后学习时候,再回头来再看这一点。但是你记住它就是tan(θ1+θ2) 就行了。
有关时间的问题
OK,那么刚才我们谈到了什么空间啊、 时间啊、 光速等等,其实里面有一个很重要的一个问题就是时间,时间不好理解,时间也不好测量。比方说我们手里如果只有一块手表的话,你会发现你知道时间是多少,可是如果你手里面有好几块钟表的话,那么几块钟表的时间不一样的时候,你突然发现你懵了,就说你不知道到底时间该是多少。你们注意你们现在大家互相之间说时间都用的是手机,大家所有的人手机会发现时间是一样子的,你好像感觉不到这个问题,那是因为我们的手机是接收的是同一个标准,所以说它才告诉大家相同的时间,而从前如果我们大家戴手表的话,你会发现手表同一时刻大家的手表上面好像显示的时间都不一样。那么在这个19世纪中期末期的时候,那时候钟表业刚兴起不太久的时候,那时候可要命了。据说法国它的市政厅时间和火车站的时间就都是不一样子的,所以这个时候就有一个很麻烦的问题,就是我的时间怎么统一,你家有块手表 我有块钟表,可是我们的钟表怎么能够显示相同的时间?这是个很重要的问题,就是钟表校准的问题,那么怎么校准呢?我们怎么去和远方联系呢?这也是我今年在跨年演讲里说的一个非常重要的观点,就是光是我们和远方唯一的联系,我们坐在这个位置上,要想和远方有联系,我们唯一的一个可以用来的工具就是光。
所以说我们要想给两块钟表,要他们给它校准显示相同的时间的话,我们能用的东西唯一能用的东西也是光,我们这么做:假设从这块钟表的地方发出一光信号到另一块钟表的地方给反射回来,发出去时候是t1 ,反射回来是t2,这就是我们在我们这个钟表看这一个光来回一趟所需要的时间,那么如果我们从另外的一块钟表从接收到第1个信号的时候起,让光回来再经过原来钟表反射回去,再回到它的旁边的时候,这就是它那个地方t'1 和t'2,它看到的两个时刻,从另外一个钟表看到的就是说光来回一趟所花的时间的长度,那么如果我们要求这两个钟表各自记录的光来回一趟的时间t2-t1和t'2-t'1是相等的。那么我们这两块钟表它记录同一个过程的时长就是一样的,我们这种意义上就可以说这两块钟表是校准的了。但是如果我们进一步的要求,就要求我们的钟表在任何时刻显示的数字也是一样的,这就得要求我这个第1个信号到达右侧钟表的时候t'1这个时刻应该等于(t2+t1)/2,是这样子状态的时候我这样的两块钟表静止的两块钟表它能够显示出的时间就是一样子了。我们说这两块静止的钟表是现在给校准了。
但是从实用的角度来说这个是远远不够的,因为我们最终需要校准的时间是什么,实际上反而是两块相对运动的钟表怎么校准的问题。大家想象一下如果我们从北京火车站发出一列火车,我8点发出的,我们怎么告诉上海火车站我的火车8点准时发出了,用什么?用电报——电磁波,也就是光。但是上海方面当他收到了一封电报,告诉他说我的火车8点钟从北京火车站已经开出了,他也是一脸懵,为什么呢?北京站的8点是什么意思?他也不知道。所以说正确的做法应该是:我们的钟表就是北京火车站放的一个钟表和火车上正在跑着的一个钟表它们应该之间是有某种校准关系,这样的话我才始终知道你说你那个地方钟表是8点的时候,它到底是什么意思?所以说这就有一个怎么给两块相对运动着的钟表,就一个在火车站一个在运行的火车上的钟表之间怎么校准的问题了。那么这时候就来了一个人,1905年来了一个叫阿尔伯特· 爱因斯坦的,这个在瑞士刚大学毕业不久的人,他当时的工作单位是什么呢?就是瑞士联邦专利局。

爱因斯坦和洛伦兹
狭义相对论意味着什么
那么爱因斯坦得出了这样的一个,就是洛伦兹变换以后意味着狭义相对论在1905年正式诞生了,而从此以后我们描述物理事件的所用的语言就有了改变了,就是如果我们按照狭义相对论的这一个语境来描述事件的话,我们要习惯用“4-矢量”。
什么叫“4-矢量”?这是一个带4个分量的一个量,比方说,我们说时空就是xyz和t,那么说速度, 也应该是4个分量;说动量, 也应该是4个分量。那么动量的4个分量是什么?就是这个px py pz ,那么第4项和ct相对应,实际上是能量除以c这样的一个表达式,这叫动量“4-矢量”。那么用这种“4-矢量”的方式来表达物理,你会发现许多物理就变得简单 ,而且最重要的是,它能给我们带来关于世界的新的认识。
比方说动量“4-矢量”,我们知道它是和时空“4-矢量”一样满足洛伦兹变换,所以说它的平方是不变的,那么这就给我们得出了一个重要的表达式就是E2=m2c4+p2c2,那么这个表达式大家看一看,如果动量P等于0的时候意味着什么?动量P=0意味着这个粒子是不动的 ,但是不动的时候它竟然也有能量E=mc²,这个就是大家可能在许多科普书里能看到的,这是狭义相对论标志性的公式E=mc²,但是请大家记住这个公式是普朗克1907年正式写成这个样子,而且这样的一个认识也是别人在爱因斯坦之前1905年之前也都认识到的,比方说有一个意大利人叫奥林托·德·普雷托,1903年的论文里面也有近似这样的形式。这个不重要,那么我们看爱因斯坦是怎么利用相对论的认识的。
比方说爱因斯坦,他考察一个原子向相反的方向发出两个光子的过程,他就运用相对论的原理。就是说他静止着看这个过程,应该能写出它的动量和能量怎么变,然后他让它相对原子跑起来,有个速度的话,他怎么描述这个现象?也应该有一个动量和能量守恒的过程。这两个表达式你会发现一解的时候,爱因斯坦就能得出一个了不起的结论,他说原子如果发光的时候它的质量就会减少,就有点像什么呢?就像我们如果绕着操场一边跑着一边喊的话也能减肥,所以说原子在发光的过程中它的质量要减少。那么减少多少?就说它减少的质量ΔM应该多少呢?爱因斯坦得出结论是说减少那个质量乘上c²的话,应该等于发出去的光子的整个能量,那么这个也是得出最后E=mc²的一个路径。大家看看,就是这样一个相对性的原理,就是说我们不管是静止还是运动,看一个原子发出光的过程,我们都能得出重要的结论,这个是非常重要的认识E=mc²。
当然了,狭义相对论主要是来自电磁学,我们知道时空4-矢量和这个动量4-矢量是用洛伦兹变换的,可是我们考虑的是电磁过程,电磁过程当然是电场强度磁场强度,这个问题我们发现电场强度和磁场强度的变换就比较复杂,好像不是4-矢量的,但是请大家记住,将来如果你把电磁学学深的话,用电磁4-矢量来表示电磁学的话,那么同样是形式更简单的我就不给大家细讲了。不管怎么着,相对论得出来这个一些结论,确实是深刻地影响了我们对这个世界的认识,给我们带来了许多意想不到的知识。
我再给大家举一个例子,就是时间到了1928年,右上角这位年轻人是英国的物理大神狄拉克,那么他就要用相对论的这样的一个能量和动量的公式,这个E²=p²c²+m²c⁴,来改造这个量子力学的方程,要得到相对论量子力学方程,那么在这个过程中,他需要做的一件伟大的事情,就是要做一个因式分解x²+y²,那么他要把因式x²+y²给分解成(αx+βy)²,这样一个完全平方的形式。同学们你们都知道,我们的老师会教我们没有这样的分解,那么狄拉克的老师也会教他,肯定没有这样的分解。但是狄拉克觉得现在我就需要这样的分解,我就硬分解,那么他会发现,如果是这里的αβ要满足α²=β²=1,αβ+βα如果等于0的话,那么这个因式分解就是可以的。可是没有哪个数αβ+βα=0,但是人家狄拉克数学好,单独的数是没有这样的关系的,可是用数排列的那个矩阵,就是几行几列这样的数是可能有这样的关系的,就是αβ+βα=0。

大神狄拉克
那么为了他这个问题狄拉克就要求它αβ是4行4列的矩阵,那么相应的量子力学的波函数就是应该是有4个分量的波函数,那么往下再走一步狄拉克竟然预言,这个世界上存在着反粒子,什么意思?就电子来说的话,说这个世界上不仅有电子,还存在和电子的质量一模一样但是带一个单元的正电荷的这样的粒子,那么狄拉克在1928年得出这个方程,1931年提出了这个方程,可能意味着有反粒子的。那么1932年,人们就在宇宙射线中发现了反粒子。大家想象一下,如果没有这个狭义相对论的这个能量动量表达式E²=p²c²+m²c⁴的话,人们是永远想不起来这个世界上还有反粒子的,这是狭义相对论的给我们带来了一个非常重要的革命性认识。
关于狭义相对论,你应该知道的
好, 怎么说呢?由于大家还比较年轻可能许多基础都没有,我不可能讲的太详细,我再强调一遍,我也不可能指着能让你们理解这里面的所有的细节,但是我请大家记住一些关键的思想,记住相对论的思想是说:物理定律不依赖于观察者所处的运动状态 ,不仅仅是运动状态,而且最重要的是,物理学定律的表达和你所处的参照框架和你所用的坐标系无关。
大家想象一下,其实这个要求,对数学的要求是非常高的。那么学会相对论了以后,大家也要记住就是说,这里面有一个关键的东西在起作用,就是描述光的方程或者说是麦克斯韦方程组或者说是麦克斯韦的电磁的波动方程。那么从这个方程,我们得出了一个重要的常数,这个常数叫光速。光速不是什么不变量,而是光速本身就没有参照物,这是个非常重要的。那么描述相对论 ,一 我们记住它的原理,就是不变性原理;第二就是我们要学会用4-矢量和洛伦兹变换说话,这个才是你学会狭义相对论的正确途径。请同学们千万不要着急,循序渐进今天你能记住这几个关键词就挺好了。
关于相对论我刚才介绍的这一部分,主要是在1905年前后给我们引入的认识,但是这仅仅是相对论发展的开始,接下来我会给大家介绍广义相对论,其实仅仅到了1907年爱因斯坦就认识到了他得到的这些相对论的理论有推广的必要。
下期预告:曹老师带你学习广义相对论初步


每周五、六晚 8 点
准时上线
在 哪 看
在以下各大媒体平台搜索「悟理学院」即可收看《云里 · 悟理》系列微课:
学习强国、人民日报客户端、央视频、新华网、科普中国、科学网、中国科普博览、中科院SELF格致论道讲坛、哔哩哔哩、微信公众号、腾讯新闻、腾讯看点、腾讯教育、微博、今日头条、西瓜视频、抖音、知乎、猿辅导、小猿搜题、科技学堂、青云学堂、荔枝新闻、科学少年社、看看新闻、茅以升科技教育基金会、7kid、蔻享学术(持续更新中……)
亦可通过点击「平台名称 / logo」进入对应主页收看
主办单位
中国科学院物理研究所长三角研究中心
中国物理学会科普工作委员会
出品单位
悟理学院
支持单位
中国青少年科技辅导员协会
北京青少年科技教育协会
江苏中关村科技产业园管委会
编辑:米老猫
近期热门文章Top10

