金魁:刑之所以奋也?——力是什么?【云里·悟理-第11课】


第十一课
刑之所以奋也?—力是什么?
主讲人

《云里 · 物理》系列微课简介

悟理学院的各位新老朋友们, 你们好 !在这一课呢,我接到的命题作文是“力是什么”, 我的这个题目比较奇怪,它叫“刑之所以奋也?—力是什么?”
那么我们首先来看看“力”这个汉字。我们先回溯到西周汉文,在这里面“力”它的直接形式是犁田的工具,所以我们的古人已经知道犁田要使劲儿——这就是力最早的一个模糊的概念 。

力:改变物体运动的状态
我们再来看一看,“刑之所以奋也”, 那么刑是什么意思呢?这里虽然用的是“刑法”的“刑”, 但是它是通“形状”的“形”。它是出自《墨子·经上》卷。这里还有一个“奋”字,这个字尤为关键。因为现在我们知道,力它是改变物体运动呢,还是维持物体运动,这是两种截然不同的观点。如果说,这个鸟是展翅欲飞,那么它是改变状态;如果鸟是在空中,它是要维持它的姿态,那是维持运动——这显然是截然不同的含义。

西周金文
好,我们仍然回到西周金汉文去看一看。这个“奋”呢,是一只小鸟在一个田间振翅欲飞的样子。很好 ,那也就是说《墨经》里面它的意思是说,力是什么呢,它是使一个物体改变运动状态的一个驱动力。同时期的亚里士多德,他的理解是说,力是从一个物体发射到另外一个物体,是依赖于物质而存在的。这是当时的认识。我们可以看到,他们在同时期都对力产生了兴趣。兴趣是推动物理、推动大家对自然了解的一个出发点。
亚里士多德他的出发点没有错,因为他观测到推动重物的时候,你需要使用更大的力;而推动轻的物体的时候呢,你需要用的力小一点。所以当时他就把动力和速度给联系起来了,用那个比例定律来联系起来。当时在古希腊有两个学派,一种是以亚里士多德为代表的学派,他是以主观的推断为主;还有一个学派呢,是大家可能听的得比较多的阿基米德他引导的学派,他是以科学实践为代表,在这个学派里面一个代表性的人物就是伽利略。

伽利略
把数学论证和实验方法
相结合的伽利略
我想课程上到这里时候,大家已经对伽利略非常的熟悉了。伽利略是最早提倡数学和实验方法相结合的科学家。他希望把数学论证和巧妙的实验方案给结合起来。那我们看一下伽利略的一个小球实验。他在实验之前当然是有一定的辩证思维的。亚里士多德的观点是说,“重物下落的快一点,轻的物体下落的慢一点”。那么我们可以做这样一个辩证地的思考:如果把一个重物和一个轻物绑在一起,下落更快的重物一定要拉着下来更慢一点的轻物,那么它们总的速度应该是比重物单独下落的速度要慢一点;但是呢,如果我们用一根绳把这个重物和轻物捆绑在一起 那这个重量比所谓的重物还要重一些,那按照这个观点的话,它下降的速度会更快才对——所以这已经有悖论了。
所以伽利略就开始做了一个实验。那么直接用重物下落的话,它的速度太快是没法开展实验的。他选取了一个斜面,用那个光滑的小槽让小球——青铜的小球滑下去。那么在这个实验里面,他用什么计时呢?那个时候是没有计时器的,它是用一个可以把壶凿开之后,可以漏水的漏壶来计时,通过漏水的所谓的比率来测量不同的行程花的时间。结果呢,他通过上百次的实验发现,在下降同样的距离的时候呢,它的计时是按照一个时间的平方比例来,就是比如说一的平方、 二的平方、三的平方、 四的平方这样来的。所以他就提取出一个数学的规律,也就是说小球下滑的距离是和时间的平方成正比。
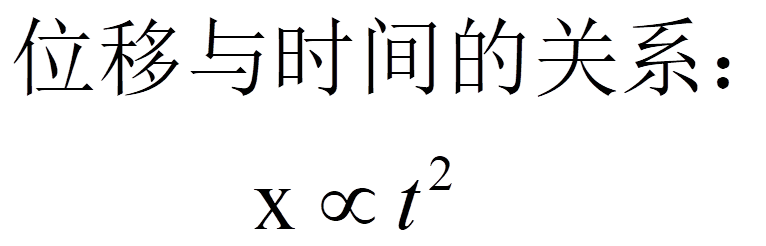
小球下滑的距离是和时间的平方成正比
现在我们知道了,这种物理的直觉图像很关键。如果说位移是跟时间的平方成正比,那也就意味着在这里面,速度是可以随着时间变化的,也就是说,自由落体的物体它不是一个匀速的运动,而是一个加速的运动。所以在这个时候“加速度”的概念也就开始浮现了。进一步,如果我们改变所谓斜面的倾斜角度,一步步地去逼近自由落体状态,那么我们就可以推出,这里的重力加速度乘以一个斜面的倾角的cosθ,就是当时小球滑落下来的加速度。
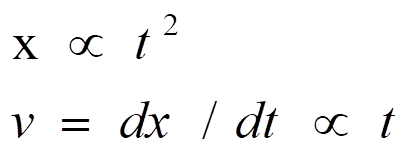
落体做加速运动遵循的规律
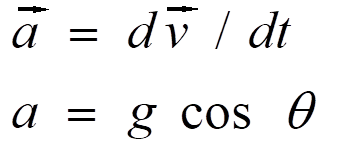
力,速度和加速度都是矢量
伽利略呢他的一生其实做了很多的实验。比如说他在教堂里面观察灯摆动的实验,发现单摆的周期与摆长的平方根是成正比的。伽利略他的这种思维方式是现在我们做物理需要的一种物理图像的一种方式,就是说我们要找出关键的物理量,并且去找出关键物理量与变量的关系这种能力。
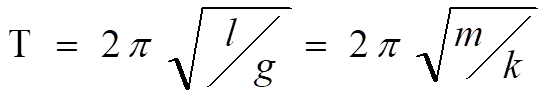
单摆的周期与摆长的平方根成正比,而与振幅大小和摆锤重量无关
伽利略他虽然是第一次提出了惯性和加速度的概念,但是他并没有摆脱一个“圆惯性”的这个思路,因为他还是没有摆脱柏拉图的“行星是做圆周运动”的这个观点。他没有能将惯性推广到一切物体运动上来。完整的惯性定律是伽利略逝世两年之后由笛卡尔来表述的。
不仅要动,还要动量
笛卡尔他是法国的科学家,他也是第一次提出了动量守恒定律。这里我们涉及的一个新的词“动量”。实际上我们知道牛顿三大定律,分别是力的定性的表达、力的定量的表达以及力是相互作用的一个本质。那么在牛顿第二定律里面,力是怎么定义的呢?它并不是我们通常所说的简单的用质量乘以加速度 ,而是用一个动量的概念,是说力是在单位时间内它动量改变的一个量。那我们下面就要去提到“动量”这个词语了。

笛卡尔
牛顿三大定律的话我们就不再细说了。动量的概念是怎么来的?我先把两个重要的事情说出来。动量的概念呢有两个关键的人物,一个是笛卡尔,刚才提到他是法国的科学家,他将动量表达为质量和速率的乘积;而牛顿呢,是把动量表达为质量和速度的乘积。提醒一下,速率是只有数值没有方向的,而速度是有方向的。
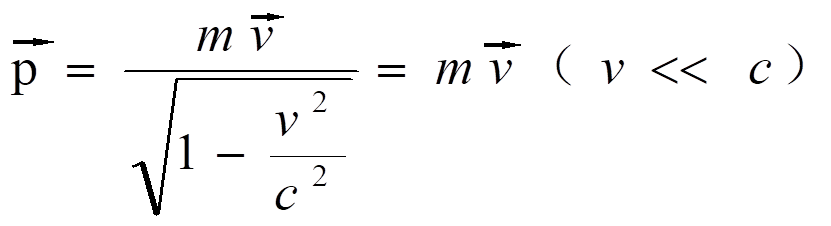
笛卡儿:动量表示为质量和速率的乘积
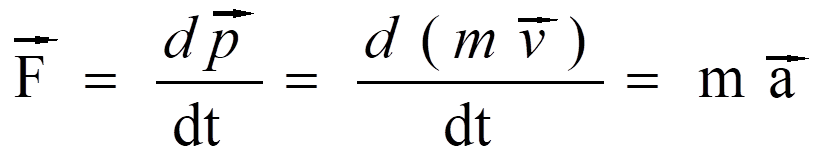
牛顿:动量表示为质量和速度的乘积
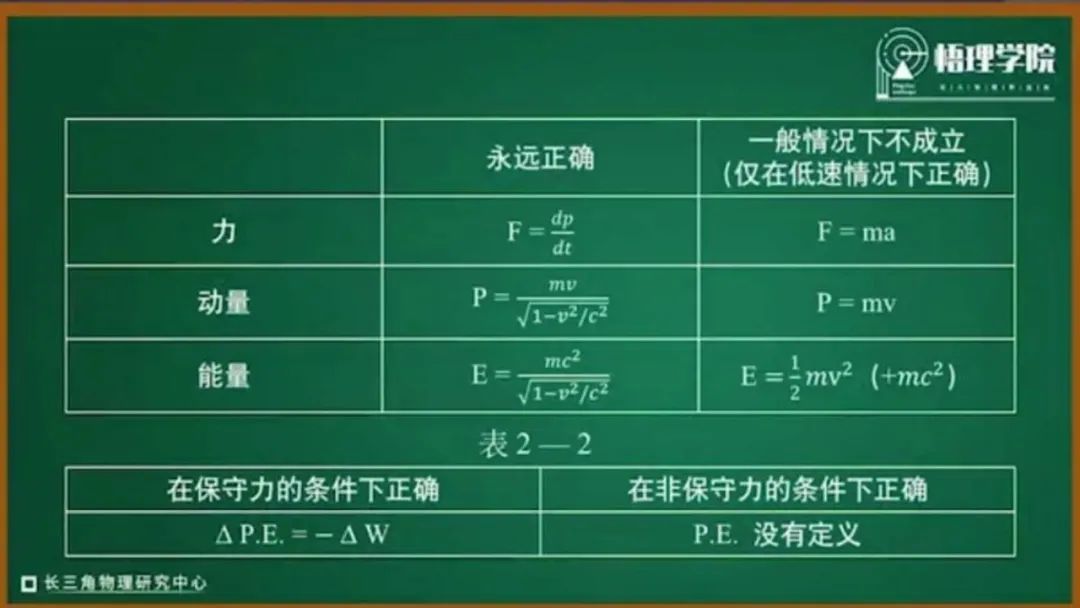
我这里一步就跨越到相对论下的一个动量表达方式,它是相当于是我们通常所知道的质量乘以速度,但是要除以一个相对论的修正因子。当速度远小于光速的时候,那么我们可以认为动量是等于质量乘以速度的。动量也是有方向的,它的方向和速度的方向是一致的。这样牛顿第二定律的表达就可以写成动量对时间的一个变化关系了,也就是说d(mv)/dt 。
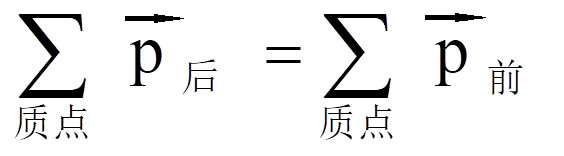
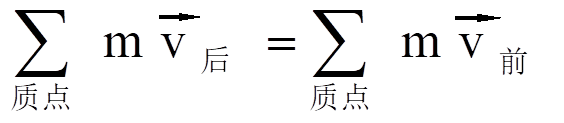
低速时,动量守恒定律
为什么要提出动量这个概念呢?是因为在古代的时候呢,人们已经意识到了,宇宙中应该有些量是不变的,是守恒的,否则的话当你停下来之后,不可能再运动起来。

牛顿摆
我这里以一个牛顿摆来把动量给引出来。我们先不要考虑时间的顺序了,那么对一个五个小球并列摆在一起的牛顿摆,当你把最左边的小球拉起来的时候,让它下落下去,当它碰到第二个小球的时候,它有一定的速度了,你会发现这个实验做出来的时候呢,它是最右边的小球动起来了,而且这个小球能够爬到那个高度和第一个碰它的小球是一样高的。也就是说从这个事件上观察来看呢,左边小球的速度好像是传递到同样质量的右边小球上去了。所以这里也就涉及到速度和质量的乘积是一个可以守恒的量 。这样的话,动量守恒定律也就出来了。
它怎么来定义的呢?我们这样来定一下,因为我们所研究的都是质点体系,那么我们把一个体系里面的质点的质量和它们相应的速度做求和,在碰撞之前和碰撞之后它所得的动量应该是不变的。这就是所谓动量的概念。
为什么从笛卡尔到牛顿,它的动量是从速率到速度这样的一个理解呢?我们可以做个简单的思考,这是因为在笛卡尔之后,荷兰的一个科学家惠更斯,他在做小球碰撞试验的时候发现,如果是用质量乘以速率的话,他发现这里面的动量是不守恒的。那么动量守恒定律它显然有更大的适用范围的,它大到天地间的相互作用,小到质子中子等基本粒子相互作用都是适用的。
那么我们再来看一看,怎么去理解所谓动量定律。它实际上是揭示了一个物体动量的变化的原因以及量度。我们打个比方,一个运动员他蹬地的力量越大、能够维持蹬地的时间越长,那么他能弹跳的高度就越高。这里面反映的例子是他蹬地的作用力的反作用力乘以时间,是等于他能够得到的动量。这就是典型的冲量方程:力量乘以时间等于质量乘以速度。那么这样的话,我们对动量有了一个更深的了解——它实际上是力在时间上的一个累积。
除了动量守恒,
还需要能量守恒
仅仅有动量守恒,我们是不是解决所有的事情了呢?那显然不是。回到刚才的牛顿摆,这里面要维持动量守恒的话,其实有很多状态。为什么不是一下子撞起两个小球呢,让这两个小球同时以一半的速度往前运动呢?为什么不是撞起四个小球,让这四个小球以四分之一的速度去往前运动呢?显然这个时候动量都是守恒的。那实际观察你会发现,理想的实验只是有一个小球以相同速度动起来了,那这是因为这里面还有一个能量守恒的概念。
同样能量守恒是什么意思呢?我们依然从相对论的方式出发给出能量的定义,那么能量是等于质量乘以光速的平方,除以一个相对论的修正因子。同样在低速下,它可以演化为一个静能和一个动能,静能就是mc2,动能就是1/2 mv2。如果我们考虑在这个系统里面,它的动能是守恒的,在这个时候,我就可以把它改成两个表达式,首先碰撞前后的质量是不变的,其次按照我们刚才所说的,多质点体系对碰撞前质点的所有的动能的求和,应该等于碰撞后所有动能的求和。那么动能是什么呢?在这里我们写成了1/2 mv2。它和动量不一样,动量是个矢量,而动能是个标量。它是一个状态量。
那么光看1/2 mv2 ,我们仍然不是太了解动能和动量的关系。这个时候我们就需要先提一下“能”。究竟什么是能量?我们从自然界可以看到,我们有热能 ,有电能,有潮汐能,有弹性势能,有核能还有太阳能等等,这是我们对能的认识。那么从能量的角度来描述的话,我们知道一个从高处落下来的重物,它的势能可以转化为动能。

自然界中的各种能量
这里我们又引入了势能的概念。没关系,我们可以用一个例子来阐述什么是动能,什么是势能,以及它们之间的关系。我们仍然是以牛顿摆去做这个相应的的验证,如果说这里给出两个限制条件,既有动量守恒,还有我们提出来的动能守恒——实际上它更标准的定义应该是能量守恒。但是呢,这里我们知道,左边一个小球开始下落的高度,和右边一个小球它弹起最大的高度是一致的。那么势能是什么呢?势能是相对于一个保守力而言的。保守力理解起来相应有点困难,但也不是不可去追溯的。保守力是什么意思呢?也就是说当我把一个物体从A推到B的时候,如果这个里面有摩擦力,我把时间倒流,那么你会发现,当它作为一个循环回来的时候呢,我还仍然要做功, 把它推回来;但是呢,你把一个小球从低处推到高处,让它有一个势能,让它再降落回来的时候,这个过程它是没有能量损耗的。所以在理解动能和势能的时候呢,我们先要提到保守力和耗散力,那么显然对于重力而言的话,它是一个保守力,也就是说你把它推到一定的高度,有一定的势能,这个势能让它再下降,降落下来的时候呢,它仍然会回到你推它之前的速度。这是一个保守力的一个概念。
对一个保守系统而言的话,如果说一个保守系统中,所有的作用力都是保守力——你可以是重力,也可以是其它的作用力,比如说电荷间的相互作用力,它也是一个保守力——那么这个时候经过一个循环,它是没有能量变化的。当你遇到一个体系里面存在耗散力的时候,我们要格外地小心,因为这个时候有可能就没有势能这个概念。比如说摩擦力,它就没有对应的摩擦势能这个说法,但是重力,我们有重力势能;电荷之间的库仑相互作用力,也有相应的势能概念;磁矢势也有相应的概念。所以我再强调一遍,耗散力怎么去判断:也就是说这个力在使物体运动过程当中 ,从a点到b点再回到a点的过程当中,它是有能量耗散的。
现在我们有了力的基本概念,它在对低速运动的物体而言的话,可以表达为质量与加速度的乘积。它有方向、 有大小,不能脱离物体而单独存在。
“牛顿力”有多大?
在国际单位制中,力的基本单位是牛顿,1 N = 1 kg · 1 m/s2。那么一牛顿究竟有多大?我们可以鸡蛋来举例。两枚鸡蛋大约是100克,在北京地区的重力加速度大概是9.801m/s2。那么做个简单的乘法,你可以发现它恰好是一牛顿。也就是说两枚鸡蛋自由落体受(重)力就是1 N。
从宏观认识到微观图像
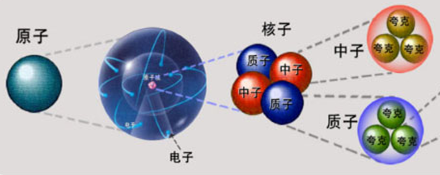
前面都是对力的一个宏观的一个认识。那么我们知道,(对于)力的微观(认识)而言的话,自然界中存在着四种基本的作用力,也就是说除了这四种基本作用之外,其他的你所认为的作用力都可以还原到这四种基本作用力上。那么在导论中向涛院士已经讲过了,这四种基本作用力分别是引力相互作用、电磁力相互作用、强相互作用和弱相互作用。前面讲了很多概念性的东西,而对物理的整个认识状态呢,是逐步深入的。下面我想举几个例子来说明我们如何加深对宏观力的微观认识。
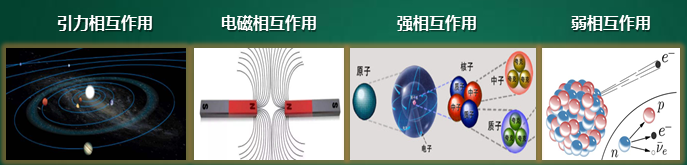
四种基本作用力
首先我想举的是冰融化成水的问题。我们常见的问题是说,冰块漂浮在水面,当这些冰完全熔化之后,水面会怎么变?答案当然是不变,因为你排出去的水和这些冰,它的重量正好是相同的。而冰熔化成水之后,它是同一种物质。那么我们紧接着要问的问题就是冰融化成水之后体积为什么会缩小?这里涉及的是一种氢键。氢键是什么呢?它本质上是一种电磁相互作用力,当冰融化熔化成水的时候,这种氢键被不停地打断,所以它的体积会缩小。但是当你超过四摄氏度的时候呢,膨胀会起主导作用,所以水在四摄氏度的时候呢,密度最大。这个例子可以告诉我们,在一个简单的问题里面,从不同的角度去问问题,你可以从宏观到微观去。
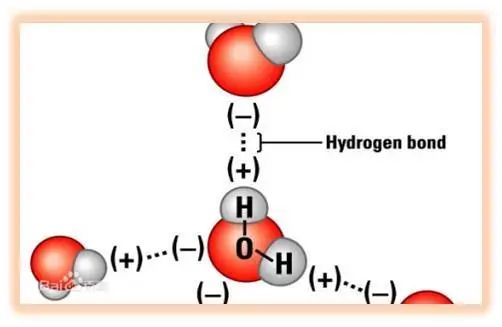
冰化水时氢键断裂
我想举的第二个例子是雄鹰展翅翱翔的例子。它也是飞机飞行的原理,从宏观上来看是它通过扇动翅膀拍动空气,让空气给它一个向上的浮力,和它自身重力抵消这样一个过程。那么它的微观机制是什么呢?这主要是因为,当你没有给定的一个速度方向时,空气中的分子它是向各个方向都会运动的。也就是说你拿一片纸在这里的时候,左边和右边给了这些分子碰撞的作用力统计上来说是可以抵消的。当你定向吹动一个空气的时候,那么你会让沿着这个方向的空气运动速度变快,那么其他方面其它方向的气体分子会减少。这就是说,这个时候你会导致向垂直方向上有个相互作用力——这也就是伯努利原理的微观思考,也是飞机飞行的原理。它同时也是为什么要求我们在快速运动的物体接近时要远离它。因为当它高速运动的时候,跟它相垂直的方向会有一个压力,使它不由自主地靠近这个物体。

雄鹰
第三个例子是大家可能在视频当中常见的超导磁悬浮的例子。你会发现这个超导体,它好像克服着自身重力一样,可以保持一个旋转悬浮的状态。那么这个里面的受力分析更加复杂了。因为它涉及到一些宏观的量子效应。因为在这里面进入超导体里面的磁通,是以量子的形式出现的。

超导磁悬浮
给四种基本作用力
串起来整一个“串烧”
我们知道恒星是一个高温的等离子体球,那么它内部的热核聚变和引力相抗衡让它不至于塌缩。
万有引力
但当恒星走向死亡的时候,变成白矮星的时候,首先它遇到第一层障碍是电子的简并压,就好比是我们要压这个桌子的时候,那么桌子为什么不变形呢?是因为我们受到的第一层防御线是电子的简并压。电子简并压本身也是一种电磁相互作用力,而且涉及量子统计,也就是费米子的统计规律。
电磁力
那么当你破坏了电子简并压,能够进一步塌缩的时候,也就是我们说的中子星 。这个时候会涉及到中子简并压这个概念,这里面会涉及到一个反β衰变。反β衰变是指电子和质子,通过反β衰变而成为中子和中微子,那么最终这个星球会变成一个中子星的气体。那么最近还有人提到了,当你突破第二层防线,即中子简并压的时候,你是否可以把中子再给打碎成为夸克星呢?那这里面涉及的就是强相互作用。
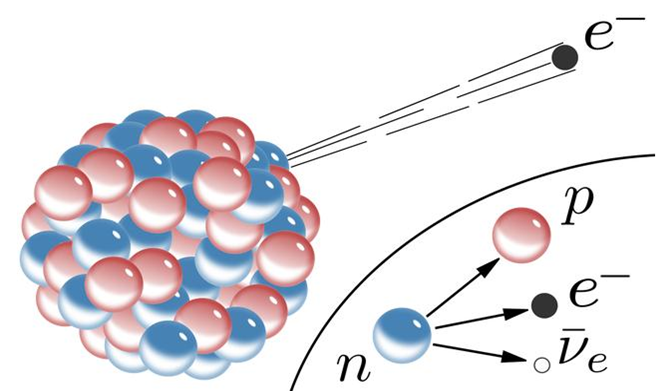
弱相互作用
强相互作用
你可以看到这个有趣的例子把引力、 电磁相互作用力、 弱相互作用和强相互作用给串起来。
那么以上就是我跟大家交流的基本内容。首先我给大家介绍了基本的概念,它们是怎么从定性到定量化的。然后呢我给大家讲述了从宏观力到微观力的认识,这种思维是启发性的、是持续性的。
我今天讲所有内容可以总结为一个简单的图表:力的表达式、动量的表达式、能量的表达式以及保守力。希望在这堂课通过我的介绍,能够形成你对力的基本概念,在以后的学习过程当中能够加深对力的印象。
学无止境,我们希望通过这堂课你能受益。本节课就到这里,谢谢大家!
下期预告:


每周五、六晚 8 点
准时上线
在 哪 看
在以下各大媒体平台搜索「悟理学院」即可收看《云里 · 悟理》系列微课:
学习强国、人民日报客户端、央视频、新华网、光明网、中国教育电视台、科普中国、科学网、中国科普博览、中科院SELF格致论道讲坛、哔哩哔哩、微信公众号、腾讯新闻、腾讯看点、腾讯教育、微博、新浪新闻、今日头条、西瓜视频、抖音、知乎、猿辅导、小猿搜题、科技学堂、青云学堂、荔枝新闻、科学少年社、看看新闻、茅以升科技教育基金会、7kid、蔻享学术(持续更新中……)
亦可通过点击「平台名称 / logo」进入对应主页收看
主办单位
中国科学院物理研究所长三角研究中心
中国物理学会科普工作委员会
出品单位
悟理学院
支持单位
中国青少年科技辅导员协会
北京青少年科技教育协会
江苏中关村科技产业园管委会
近期热门文章Top10

