图源:pixabay.com
撰文 | 张天蓉
责编 | 吕浩然
玻尔兹曼作为统计力学大师,研究的是经典粒子的统计行为,那么,量子力学中粒子的统计行为又是怎么样的?为何与经典粒子统计规律不同呢?这段历史将再次让我们的目光返回到旧量子论的年代。
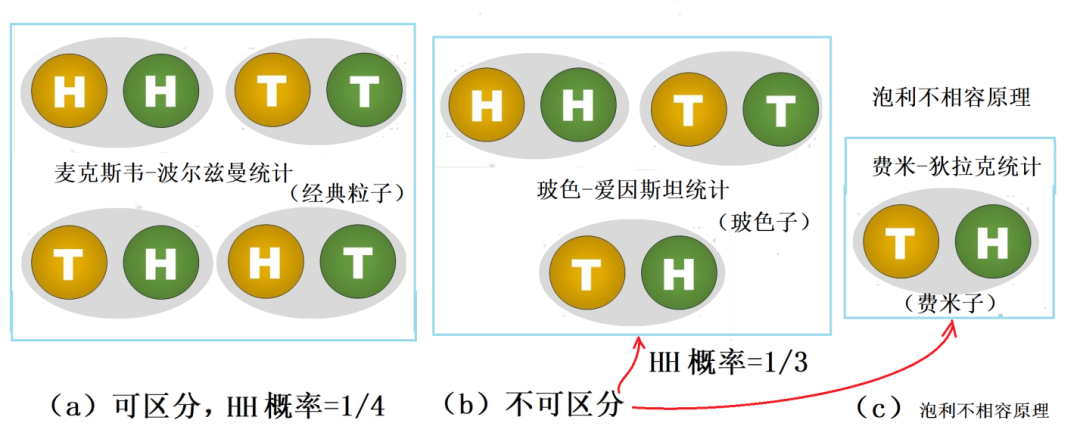
现代物理学观点认为量子统计的规律有两种:玻色-爱因斯坦统计和费米-狄拉克统计。这四位物理学家中的爱因斯坦是人人皆知的大神,费米和狄拉克也都在诺贝尔奖榜上有名,可这个玻色和费米是谁呢?本篇我们就介绍一下玻色和费米两位学者。玻色的确不是那么有名,印度人,属于第三世界的物理学家,固然受很多条件所限。不过,由他而命名的玻色子在物理学界还是挺有名的。对玻色子统计规律的研究是玻色一生中唯一一项重要的成果。有趣的是,玻色是因为一个“错误”而发现玻色子统计规律的。1921年左右,在一次有关光电效应的讲课中,玻色犯了一个类似“掷两枚硬币,得到两次正面(即‘正正’)的概率为三分之一”的错误。没想到,这个错误却得出了与实验相符合的结论,也就是不可区分的全同粒子所遵循的一种统计规律。什么叫“掷两枚硬币,‘正正’概率为三分之一”的错误?另外,什么叫“不可区分的全同粒子”?两个粒子可区分或不可区分,会影响概率的计算吗?我们看看在现实生活中如何计算概率。如果我们掷两枚硬币,因为每个硬币都有不同的正反两面,所有可能的实验结果就有四种情况:正正、正反、反正、反反。如果我们假设每种情形发生的几率都一样,那么,得到每种情况的可能性皆是四分之一。现在,想象我们的两枚硬币变成了某种“不可区分”的两个粒子,姑且称它们为“量子硬币”吧。这种不可区分的东西完全一模一样,而且不可区分。既然不可区分,‘正反’和‘反正’就是完全一样的,所以,当观察两个这类粒子的状态时,所有可能发生的情形就只有“正正”“反反”“正反”三种情形。图2:“可区分”和“不可区分”粒子的统计规律不一样
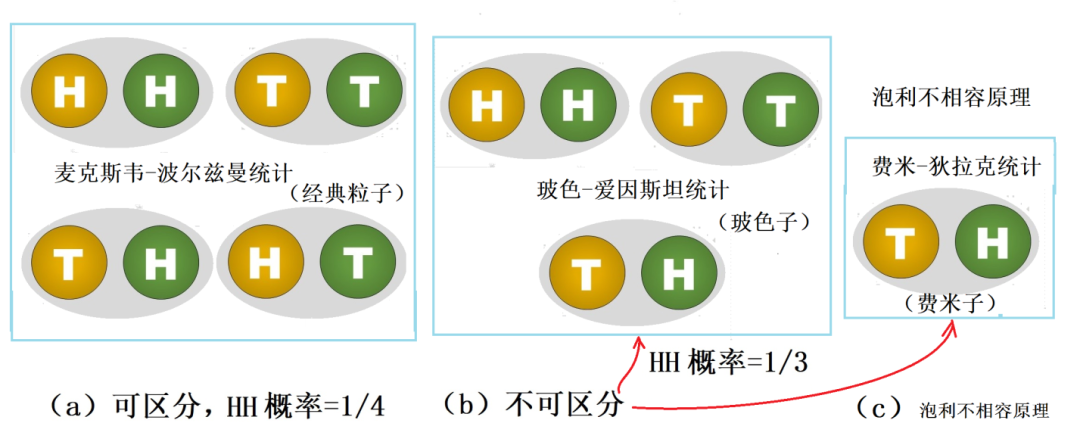
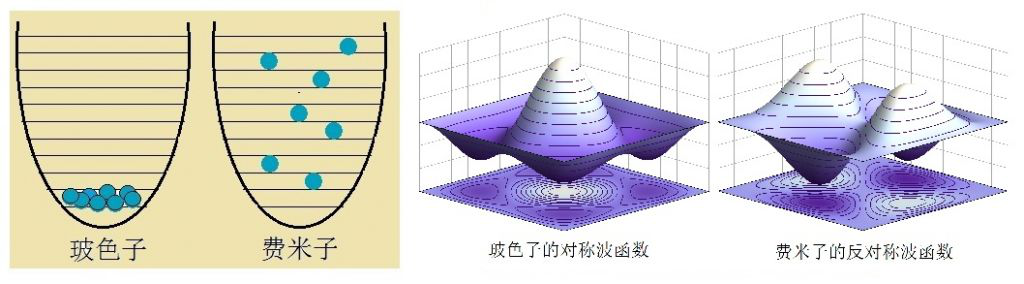
这时,如果我们仍然假设三种可能性中每种情形发生的几率是一样的(尽管这好像不太符合我们对于实际“硬币”的日常经验,但不要忘记,我们考虑的是某种抽象的“量子硬币”),我们便会得出“每种情况的可能性都是三分之一”的结论。这个例子就说明了,多个“一模一样、无法区分”的物体,与多个“可以区分”的物体,所遵循的统计规律是不一样的。纳特·玻色(Nath Bose,1894 - 1974)出生于印度加尔各答,他的父亲是一名铁路工程师,他是七名孩子中的长子。玻色在大学时得到几位优秀教师的赞赏和指点,但他只得了一个数学硕士,并未继续攻读博士学位,就直接在加尔各答物理系担任讲师职务,后来又到达卡大学物理系任讲师,并自学物理。大约1922年,玻色讲课时讲到光电效应和黑体辐射时的紫外灾难,他打算向学生展示理论预测的结果与实验的不合之处。那时候,新量子论(量子力学)尚未诞生,已经使用了二十多年的旧量子论,不过是在经典物理的框架下,做点量子化的修补工作。至于粒子的统计行为,需要应用统计规律时,仍然是波尔兹曼的经典统计理论。物理学家们的脑袋中,绝对没有所谓粒子“可区分或不可区分”的概念。每一个经典的粒子都是有轨道可以精确跟踪的,这就意味着,所有经典粒子都可以互相区分!玻色也是一样,他想对学生讲清楚黑体辐射理论与实验不一致的问题。于是,他运用经典统计来推导理论公式,但是,他在推导过程中,犯了我们在上面所述的那种“错误”,简单而言,就是将丢两枚硬币时出现“正正”的概率,误认为是三分之一。但是,万万没想到这个偶然的错误却得出了与实验相符合的结论。为什么数学错误反而得到正确物理结论?此事蹊跷。聪明的玻色立刻意识到,这也许是一个“没错的错误!”他继续深入钻研下去,研究概率1/3区别于概率1/4之本质,进而写出了一篇《普朗克定律与光量子假说》的论文。文中,玻色首次提出经典的麦克斯韦-波尔兹曼统计规律不适合于微观粒子的观点。他认为是因为海森堡的不确定原理构成的影响,使得需要一种全新的统计方法。然而,没有杂志愿意发表这篇论文,因为他们都认为玻色犯了当时统计学家看来十分低级的错误。后来的1924年,玻色突发奇想,直接将文章寄给大名鼎鼎的爱因斯坦,不料立刻得到了爱因斯坦的支持。玻色的“错误”之所以能得出正确结果,因为光子正是一种不可区分的、后来被统称为“玻色子”的东西。对此,爱因斯坦心中早有一些模糊的想法,如今玻色的计算正好与这些想法不谋而合。爱因斯坦将这篇论文翻译成德文,并安排将它发表在《德国物理学期刊》。玻色的发现是如此重要,以至于爱因斯坦写的一系列论文,称它为“玻色统计”。因为爱因斯坦的贡献,如今,它被称为“玻色-爱因斯坦统计”。之后又有了超低温下得到“玻色-爱因斯坦凝聚”的理论。这可以说是一个诺奖级别的工作,但遗憾的是玻色本人像一颗划过天空,闪亮一时又转瞬即逝的彗星一样,之后在科学上没有大作为,最终与诺奖无缘,1974年于80岁高龄死于加尔各答。玻色的“错误”能得出正确结果,正是因为光子是不可区分的。这种互相不可区分的、一模一样的粒子在量子力学中叫做“全同粒子”。所谓全同粒子,就是质量、电荷、自旋等内在性质完全相同的粒子。在宏观世界中,可能不存在完全一模一样的东西,即使看起来一模一样,它们也是可以被区分的。因为根据经典力学,即使两个粒子全同,它们运动的轨道也不会相同。因此,我们可以追踪它们不同的轨道,进而区分它们。但是,在符合量子力学规律的微观世界里,粒子遵循不确定性原理,没有固定的轨道,因而无法将它们区分开来。量子力学中,有两种类型的全同粒子:玻色子和费米子,分别以玻色和费米两位物理学家命名,它们分别服从两种不同的量子统计规律。图4:“可区分”和“不可区分”粒子的统计规律不一样光子就是玻色子。不可区分的全同粒子算起概率来的确与经典统计方法不一样。如图4a所示,对两个经典粒子而言,出现两个正面(HH)的概率是1/4,而对光子这样的玻色子而言,出现两个正面(HH)的概率是1/3(图2b)。在图4c中,我们图示了玻色子和费米子的区别。费米子也是全同粒子,它是符合泡利不相容原理(两个电子不能处于同样的状态)的全同粒子,比如电子。我们仍然以两个硬币为例,可以说明费米子的统计规律有何特别之处。假设两个硬币现在变成了“费米子硬币”,对两个费米子来说,因为它们不可能处于完全相同的状态,所以,四种可能情形中的HH和TT状态都不成立了,只留下唯一的可能性:HT。因此,对两个费米子系统,出现HT的概率是1,出现其它状态的概率是0。 研究费米子统计规律的功劳,要归于美籍的意大利裔物理学家恩利克·费米(Enrico Fermi,1901-1954)。以费米名字命名的物理对象很多:费米子、费米面、费米-狄拉克统计、费米悖论……甚至还有100号化学元素“镄”。当然,还有大名鼎鼎的美国芝加哥费米实验室、芝加哥大学的费米研究院等等。但了解费米其人的大众却不多,这是因为费米一生处事低调,淡泊名利。费米主要成就包括首创β衰变的定量理论,设计并建造了世界上第一台可控核反应堆等等。费米是1938年诺贝尔物理学奖获得者,他对理论物理和实验物理均做出了重大贡献,因而被称为现代物理学的最后一位通才。费米作为家中最小的孩子,童年的他身材瘦小、不爱说话,看上去缺乏想象力,甚至不够聪明。但这似乎又一次印证了中国的那句老话:大智若愚。看看费米一生的成就、在物理学上的造诣就明白了。10岁的费米就能独立理解表示圆的公式X2+Y2=R2,他很小就熟练地掌握了意大利语、拉丁语和希腊语;18岁时,他因为一篇《声音的特性》的论文引起了物理学权威们的关注;1929年,未满30岁的费米成为意大利最年轻的科学院院士。作为院士的费米知名度提升,但他为人仍然十分低调。据说有一次,费米和妻子一起到一家旅馆,老板问他是不是费米院士“阁下”,费米随口回答说自己是那个费米院士的远房亲戚。也没有人质疑费米在30岁就成为意大利科学院院士是否太年轻,因为他在25岁时就发现了我们前面介绍的费米子遵循的量子统计。1926年,费米和狄拉克各自独立地发表了有关这一统计规律的两篇学术论文。两位科学家都很低调谦虚,狄拉克称此项研究是费米完成的,他将其称为“费米统计”,并将对应的粒子称为“费米子”。不同微观粒子的全同性统计行为有所不同,而这种不同则来源于它们的自旋,以及自旋所导致的不同的对称性。玻色子是自旋为整数的粒子,比如光子的自旋为1。两个玻色子的波函数是交换对称的,当两个玻色子的角色互相交换后,总的波函数不变;而费米子的自旋则是半整数的,比如电子的自旋是二分之一。由两个费米子构成的系统的波函数是交换反对称的,即当两个费米子的角色互相交换后,系统总的波函数只改变符号。(见图5中的右边二图)反对称的波函数与泡利不相容原理有关,所有费米子都遵循这一原理。因而,原子中的任意两个电子不能处在相同的量子态上,而是在原子中分层排列(见图5中的左边二图)。在这个基础上,才得到了有划时代意义的元素周期律。图6:玻色子和费米子的不同特性源于不同的自旋波函数
因为玻色子喜欢大家同居一室,大家都拼命挤到能量最低的状态。比如,光子就是一种玻色子,许多光子可以处于相同的能级,所以我们才能得到激光这种超强度的光束。那么,原子呢?原子是复合粒子,情况要复杂一点。对复合粒子来说,如果由奇数个费米子构成,则这个复合粒子为费米子;由偶数个费米子构成,则为玻色子。如果将玻色子的原子,在一定的条件下,温度降低到接近绝对零度,所有玻色子会突然“凝聚”在一起,那时会产生一些常态的物质中观察不到的“超流体”的有趣性质,这被称为“玻色-爱因斯坦凝聚”。通过对“玻色-爱因斯坦凝聚”的深入研究,有可能实现“原子激光”之类的、前景诱人的新突破。因此,全同粒子的玻色子或费米子行为,是量子力学最神秘的侧面之一。 正好在费米获得诺贝尔奖的那一年,意大利的墨索里尼(Benito Amilcare Andrea Mussolini,1883 -1945)开始逮捕和迫害犹太人。因为费米的夫人是犹太人,所以费米便利用到瑞典领奖的机会,举家逃到了美国,并在哥伦比亚大学任教。1941年底,在爱因斯坦等人的提议下,美国政府决定启动名为“曼哈顿”的原子弹研制计划,费米成为主要的参与者之一。他指挥建造了世界上第一座“人工核反应堆”,并将它秘密转移到新墨西哥州洛斯阿拉莫斯峡谷附近,最终在1945年的7月12日制成了世界上第一颗原子弹。四天后,这颗原子弹被成功引爆。科研生涯的最后几年,费米还从事高能物理的研究。天妒英才,正值事业巅峰期的费米在食道癌和胃癌的双重打击下,于1954年11月28日逝世于芝加哥的家中,时年53岁。原标题:量子统计:玻色与费米 | 量子群英传
来源:赛先生

编辑:小林绿子
近期热门文章Top10