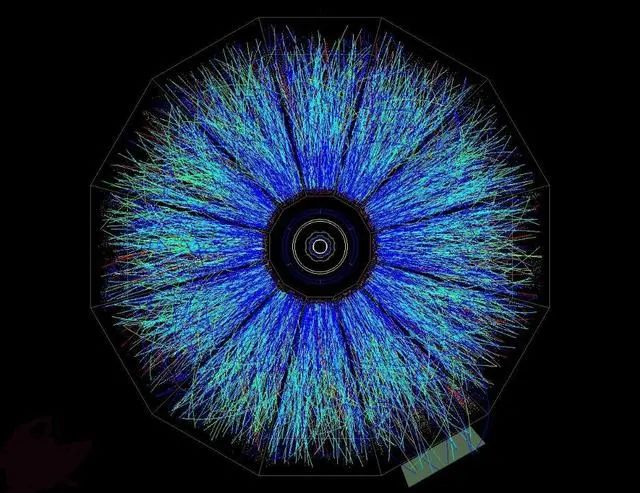
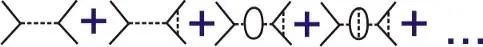物理学家说,我们生活在一个全息图中,但他们的意思是什么?房间的墙上是否有一个平面世界的我?或者我是一个神秘的五维存在的投影,超出了我自己的理解?如果我脑子里的所有东西都可以用它的边界来描述,那么我实际生活在多少个维度中?如果这些问题让你夜不能寐,我有答案。1.为什么有些物理学家认为我们的宇宙可能是一个全息图?
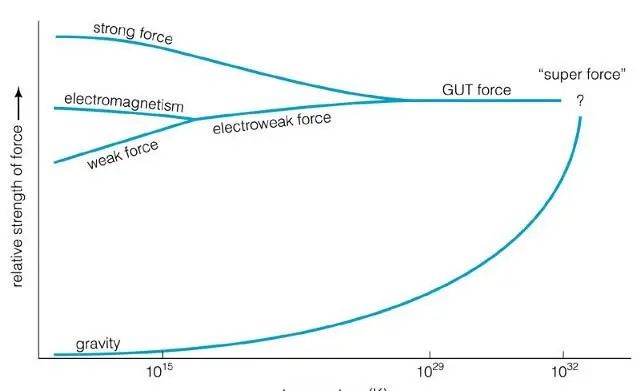
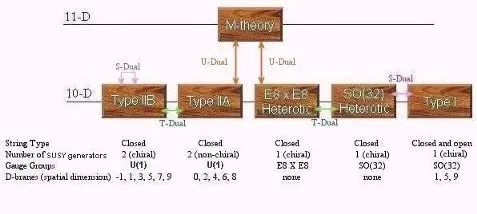
统一对我们理解自然规律非常有用:苹果的下落规律与行星的运行规律相同。物质以气体、液体和固体的多种形式出现,可以用分子的不同排列方式来描述。分子的巨大变化本身可以被理解为原子的各种组成。这些统一的原则很久以前就被发现了。今天,物理学家将统一称为不同相互作用的共同起源。例如,电和磁的相互作用被证明是同一电磁相互作用的两个不同方面。电磁相互作用,已进一步与弱核相互作用统一起来。目前还没有人能成功地将所有已知的相互作用统一起来,包括电磁作用、强核作用和弱核作用,以及引力作用。弦理论被认为是强核相互作用的理论,但很快就发现量子色动力学,即夸克和胶子理论。在物理学家发现弦可以用来解释所有已知的相互作用,包括引力之后,使用弦的想法获得了重生,因此可以成为万物的统一理论,物理学的圣杯。然而,要从弦理论中得到具体相互作用的标准模型是很困难的。所以这个故事是这样的,近年来,对统一的追求慢慢被对二元性的追求所取代,这表明所有不同类型的弦理论实际上是同一理论的不同方面,这一点还没有被完全理解。一般意义上的二元性是一种确定两种理论的关系。你可以把二元性理解为一种特殊类型的统一。在正常的统一中,你将两个理论合并成一个更大的理论,在一个合适的范围内包含前两个理论。如果你把两个理论通过对偶性联系起来,你会发现理论是一样的,只是它们看起来不同,这取决于你怎么看它们。在过去几十年里,高能物理学最有趣的发展之一是在不同数量的时空维度中发现理论之间的二元性。其中一个理论是高维空间的引力理论,通常被称为“体积”。另一种是与标准模型非常相似的测量理论,它存在于体积时空的边界(有时被称为“膜”)上。这种关系通常被称为测量重力对应关系,它是弦理论中更普遍的对偶性的一个极限。请注意,这种对应关系还没有得到严格的证明。但是,有几个例子已经进行了充分的研究,因此几乎可以肯定地证明了这一点。这些二元性被称为“全息”,因为它们告诉我们,在引力理论的大部分时空中,所有允许发生的事情都被编码在那个空间的边界上。因为在体积表面的信息比体积本身的信息少,所以在体积中发生的事情比你预期的要少。似乎盒子里的粒子都是相互独立的,但它们实际上是相互关联的。就像您正在观察一个大房间,孩子们在奔跑和跳跃一样,但是突然之间,您会发现他们中的每一个跳跃,出于神秘的原因,十个人必须在同一时间跳跃。◉如果你在体积和表面上用离散的单位来编码信息,看起来你可以在体积中存储比在表面上更多的信息。全息术告诉你事实并非如此。并不是体积中的所有构型都是独立的。
由于全息技术,对粒子之间的独立性数量的这种限制只会在密度太高而无法直接测试的情况下变得明显。但是,这种对偶性之所以有趣,是因为物理学主要是熟练的近似技术,而使用对偶性是一项新技能。你们可能见过费曼图,它们描绘了粒子散射过程,这些图中的每一个都对交互过程有贡献。图中的循环越多,贡献就越小。所以物理学家所做的就是先把最大的贡献加起来,然后是较小的,然后是更小的,直到它们达到预期的精度。它被称为“微扰理论”,只有在相互作用越多,贡献越小的情况下才有效。如果是这样,这个理论就被称为“弱耦合”,一切都很好。如果不是这样,这个理论就被称为是“强耦合的”,你永远不可能把所有相关的贡献加起来。如果一个理论是强耦合的,那么粒子物理学家的标准方法就失败了。例如,强核力具有“渐近自由”的特殊性质,这意味着它在高能量下会变弱。但在低能量时,它非常强。因此,人们对低能的核物质理解得很差,例如夸克胶子等离子体的行为,或者为什么单个夸克不能自由运动,却总是“局限”在更大的复合态中。另一个有趣的例子是“奇怪”金属,其中包括高温超导体,这是物理学家的另一个圣杯。当一个理论强耦合且难于处理时,对偶理论弱耦合且易于处理,因此测量-重力对偶性有助于处理这些系统。对偶性本质上是把一个困难的计算转换成一个简单的计算。由于边界理论和整体理论是由对偶性联系在一起的,它们可以用来描述相同的物理现象。因此,在基本层面上,这种区别是没有意义的——它们是描述同一事物的两种不同方式。只是有时候其中一个更容易使用,有时候另一个更容易使用。如果你观察特定的系统,比如夸克胶子等离子体或黑洞,你可以给出这个问题的意义,并要求粒子经历的维数。粒子的这种规格说明使这个问题变得有意义,因为识别粒子并不总是可能的。夸克胶子等离子体的理论被置于边界上,因为它将由强耦合理论来描述。因此,如果您认为它是您实验室的一部分,那么您已经将自己和实验室都放在了边界上。然而,我们所体验的“维度”的概念是与粒子的自由移动联系在一起的。这可以在“光谱维数”的定义上变得更加严格,粗略地说,“光谱维数”测量的是一个粒子可以迷失在多少个方向上。使一个系统强耦合的事实意味着我们不能正确地定义自由运动的单个粒子。所以当你可以在实验室的三维空间中移动的时候,夸克胶子等离子体首先必须被转换成高维理论来讨论单个粒子的移动。从这个意义上说,实验室的一部分确实变得更高维了。◉RHIC是在相对论性重离子碰撞中产生夸克胶子等离子体的对撞机之一。然而,如果你观察一个天体物理黑洞,情况就相反了。我们知道在它附近的粒子是弱耦合的,并且只经历三维空间。如果你想在这种情况下应用二元性,那么我们就会处在整体中,会有我们的低纬度投影和边界上的黑洞。这将限制我们四处走动的自由,即使是以一种我们没有注意到的微妙方式。然而,与测量重力二元性相关的体积时空是所谓的反德西特空间,它们总是有一个负的宇宙常数。然而,就我们目前所知,我们居住的宇宙有一个正的宇宙常数。因此,目前还不清楚是否真的有一个更低维度的系统可以描述我们宇宙中的黑洞。目前,许多研究人员正致力于扩展测量重力二元性,以包括具有正的宇宙常数或根本没有的空间,但至少到目前为止,还不清楚这是否有效。所以现在我们不知道在低维度时空中是否存在我们的投影。测量重力二象性的应用大致分为三个大的领域,加上推动对该理论的一般理解的技术发展的多样性。这三个区域分别是夸克胶子等离子体、奇异金属和黑洞蒸发。在前两种情况下,我们的宇宙在边界上,在后一种情况下,我们在体积上。对黑洞蒸发的研究是对数学一致性的检验,旨在揭示信息是如何逃离黑洞的,或者在奇点处发生了什么。在这个领域,目前的问题多于答案。对偶性在夸克胶子等离子体上的应用最初引起了许多兴奋,但随着最近一些怀疑论的传播。看来等离子体并不像最初认为的那样强耦合,使用二元性也不像希望的那样简单。随着分析方法和数值方法的发展,奇异金属和其他类型材料的应用正在迅速发展。几个观察到的行为已经被定性地再现了,但是目前还不是很清楚哪种系统是最好的。模型的空间仍然太大,这为有用的预测留下了太多的空间。在这个领域,答案多于问题。全息术是一个令人难以置信的想法,从数学上讲,有大量令人信服的理由和一致性表明我们的宇宙很可能是一个全息图。但对于我们能在三维现实中观察到什么有新的见解呢?旅程仍在继续。(END)