早在远古时代，人类就已经开始将热现象引入生活和生产的重要环节从而利用热能。但直到十七、十八世纪，人们才开始对涉及热的能量转换过程进行集中的研究，这一研究领域就叫做热力学。在这一时期，焦耳、卡诺、开尔文、克劳修斯等著名的科学家对热力学中的温度、热、功等概念，以及各种热力学过程中的能量转换进行了系统的研究，并总结出了热力学的三大定律，为热力学发展奠定了理论基础。

热力学的一个重要应用便是热机。热机是一种周期性的从热源中提取热能并将其部分用于对外做功的机械装置。瓦特所改良的蒸汽机就是最早期的热机，它的出现引起了十八世纪中叶从英国发起的第一次工业革命。此后，人们基于热力学规律设计了多种多样的热机，并不断对热机的性能进行优化。因而提高了生产效率，加速了社会进步。

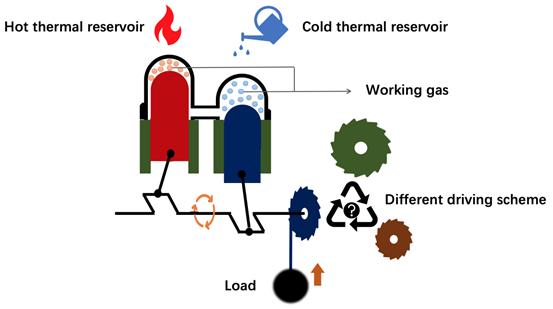
图1 热机示意图

功率和效率是衡量热机性能的两个主要参数，前者表示单位时间内热机能对外做功的量，后者代表热机能以多大比例将从热源吸收的热量转化为可用的输出功。十八世纪直至十九世纪初，受到热力学发展制约，人们在理论上讨论的热机主要是以简化的准静态工作的理想热机。卡诺的研究给出了这样一种理想的热机效率的上限，即著名的卡诺效率。十九世纪三十年代，热力学的发展从平衡态拓展到非平衡态，有限时间热力学的理论应运而生，这使得人们可以开始在理论上研究更接近现实的实际热机：运行周期有限的热机。至此，一个自然问题便是：我们能造出功率和效率都很高的热机吗？

要回答上述问题，我们来想象一个古代马车运水情景：利用马车上的开口容器从水源地把水运输到城市。由于马车运送过程的震动，水在运输途中会从开口容器中洒落一部分出来。显然为了减少运输损耗，需要尽量降低运动速度，但是这种情况下给定时间内运输的水量就会减少。具体来说，我们把单位时间内运送水量叫做,每次从水源地载入水量A与实际到城市的水量B之比A/B叫做运输效率。从这个简单的例子我们可以看出，水运输量和运输效率间存在着一定的制约关系，这一制约是由于运输途中损失的水量与运输时间相关而导致的。

上述例子中我们引入的和正好对应于热机的效率和功率。运输途中损失的水量，代表热机在有限时间内工作而损耗的能量，这一部分能量不能用于对外做功，因而会降低热机的效率。因此，从这个简单的类比和讨论来看，并不存在如此好的事情，让我们造出功率和效率均高的“超级热机”。正是由于在运行过程中的能量损失（耗散），热机的功率和效率之间存在着一定的制约关系。显然，这一制约关系对设计针对具体生产任务的最优热机十分重要。

有限时间热力学的研究表明，优化热机功率和效率的关键在于分析热机在工作中能量损失对工作时间的依赖关系。近些年的研究发现，在某些情况下（有限时间等温过程）这一能量损失与热机的工作时间恰好成反比关系。这是一个十分简洁却有用的关系，启发了一系列的理论研究。然而，我们注意到，一直以来都缺乏对这一关系定量的实验研究。最近，研究生院孙昌璞和董辉课题组设计搭建了一套气缸装置（北京计算科学研究中心博士研究生马宇翰参与设计，研究生院硕士研究生翟若迅参与搭建），利用对干燥空气的压缩过程，第一次对有限时间等温过程中的能量损失和时间的反比关系进行了检验^[1]。实验结果表明，除了与做功时间成反比外，我们感兴趣的这一能量损失还可以通过压缩空气的方式来改变。比如，在压缩时间和其它条件一定的情况下，匀速的压缩和先慢后快的压缩气体，所测得的能量损失是不同的。这为设计最优的时间热机提供了新的思路。

从20世纪后期至今，除了研究非平衡的有限时间热力学效应，热力学的发展还与量子力学结合起来衍生出了一个新的分支：量子热力学。这一新兴领域的研究目标是探究一系列的量子效应，如量子相干性、量子纠缠等是否有利于提高热机的性能。近年来，这一领域吸引了国内外相当的研究兴趣，也在理论和实验上均取得了一系列有意义的结果。孙昌璞和董辉课题组北京理工大学徐大智副教授最近在量子热力学的框架内，结合有限时间热力学的研究动机，在理论上讨论了二能级原子热机的有限时间行为，并基于此微观模型证明了前面所述的能量损失与时间及与对热机操纵方式的关系^[2-5]。我们的研究表明，有限时间等温过程中的能量损失和时间的反比关系在量子尺度依然成立。同时，我们还模拟了二能级原子热机在不同的时间周期内的工作，检验了其功率和效率间的制约关系，与基于唯相模型所推出的理论结果符合良好。未来，在微观尺度下讨论有限时间热力学问题是一个值得关注的发展方向，这会帮助我们理解小系统的非平衡热力学行为，也会为设计能在量子世界里工作的高性能热机打下理论基础。

图2 研究生院孙昌璞和董辉课题组设计搭建的气缸装置