【AI PC端算法优化】七,一步步优化RGB和YUV互转算法
以下文章来源于GiantPandaCV ,作者BBuf
专注于机器学习、深度学习、计算机视觉、图像处理等多个方向技术分享。团队由一群热爱技术且热衷于分享的小伙伴组成。我们坚持原创,每天一到两篇原创技术分享。希望在传播知识、分享知识的同时能够启发你,大家一起共同进步(・ω<)☆
1. 前言
继续学习指令集优化的知识,今天来讨论一个图像颜色空间转换经常碰到的一个问题即RGB和YUV图像的颜色空间转换,我们从原理介绍和普通实现开始,然后介绍一些优化方法并引入SSE指令集来优化这个算法的速度。
2. 原理介绍
首先介绍一下YUV颜色空间,YUV(亦称YCrCb)是被欧洲电视系统所采用的一种颜色编码方法。在现代彩色电视系统中,通常采用三管彩色摄像机或彩色CCD摄影机进行取像,然后把取得的彩色图像信号经分色、分别放大校正后得到RGB,再经过矩阵变换电路得到亮度信号Y和两个色差信号R-Y(即U)、B-Y(即V),最后发送端将亮度和两个色差总共三个信号分别进行编码,用同一信道发送出去。这种色彩的表示方法就是所谓的YUV色彩空间表示。采用YUV色彩空间的重要性是它的亮度信号Y和色度信号U、V是分离的。如果只有Y信号分量而没有U、V信号分量,那么这样表示的图像就是黑白灰度图像。彩色电视采用YUV空间正是为了用亮度信号Y解决彩色电视机与黑白电视机的兼容问题,使黑白电视机也能接收彩色电视信号。
YUV主要用于优化彩色视频信号的传输,使其向后相容老式黑白电视。与RGB视频信号传输相比,它最大的优点在于只需占用极少的频宽(RGB要求三个独立的视频信号同时传输)。其中“Y”表示明亮度(Luminance或Luma),也就是灰阶值;而“U”和“V” 表示的则是色度(Chrominance或Chroma),作用是描述影像色彩及饱和度,用于指定像素的颜色。“亮度”是透过RGB输入信号来建立的,方法是将RGB信号的特定部分叠加到一起。“色度”则定义了颜色的两个方面─色调与饱和度,分别用Cr和Cb来表示。其中,Cr反映了RGB输入信号红色部分与RGB信号亮度值之间的差异。而Cb反映的是RGB输入信号蓝色部分与RGB信号亮度值之同的差异。
接下来我们看一下RGB和YUV颜色空间互转的公式:
1,RGB转YUV
Y = 0.299R + 0.587G + 0.114B
U = -0.147R - 0.289G + 0.436B
V = 0.615R - 0.515G - 0.100B
2,YUV转RGB
R = Y + 1.14V
G = Y - 0.39U - 0.58V
B = Y + 2.03U
3. 普通实现
按照上面的公式容易写出最简单的实现,代码如下:
void RGB2YUV(unsigned char *RGB, unsigned char *Y, unsigned char *U, unsigned char *V, int Width, int Height, int Stride) {
for (int YY = 0; YY < Height; YY++) {
unsigned char *LinePS = RGB + YY * Stride;
unsigned char *LinePY = Y + YY * Width;
unsigned char *LinePU = U + YY * Width;
unsigned char *LinePV = V + YY * Width;
for (int XX = 0; XX < Width; XX++, LinePS += 3)
{
int Blue = LinePS[0], Green = LinePS[1], Red = LinePS[2];
LinePY[XX] = int(0.299*Red + 0.587*Green + 0.144*Blue);
LinePU[XX] = int(-0.147*Red - 0.289*Green + 0.436*Blue);
LinePV[XX] = int(0.615*Red - 0.515*Green - 0.100*Blue);
}
}
}
void YUV2RGB(unsigned char *Y, unsigned char *U, unsigned char *V, unsigned char *RGB, int Width, int Height, int Stride) {
for (int YY = 0; YY < Height; YY++)
{
unsigned char *LinePD = RGB + YY * Stride;
unsigned char *LinePY = Y + YY * Width;
unsigned char *LinePU = U + YY * Width;
unsigned char *LinePV = V + YY * Width;
for (int XX = 0; XX < Width; XX++, LinePD += 3)
{
int YV = LinePY[XX], UV = LinePU[XX], VV = LinePV[XX];
LinePD[0] = int(YV + 2.03 * UV);
LinePD[1] = int(YV - 0.39 * UV - 0.58 * VV);
LinePD[2] = int(YV + 1.14 * VV);
}
}
}
我们来测一把耗时,结果如下:
| 分辨率 | 算法优化 | 循环次数 | 速度 |
|---|---|---|---|
| 4032x3024 | 普通实现 | 1000 | 150.58ms |
4. RGB和YUV互转优化第一版
首先比较容易想到的技巧就是我们把上面的浮点数运算干掉,基于这一点我们做如下的操作:
Y * 256 = 0.299 * 256R + 0.587 * 256G + 0.114 * 256B
U * 256 = -0.147 * 256R - 0.289 * 256G + 0.436 * 256B
V * 256 = 0.615 * 256R - 0.515 * 256G - 0.100 * 256B
R * 256 = Y * 256 + 1.14 * 256V
G * 256 = Y * 256 - 0.39 * 256U - 0.58 * 256V
B * 256 = Y * 256 + 2.03 * 256U
简化上面的公式如下:
256Y = 76.544R + 150.272G + 29.184B
256U = -37.632R - 73.984G + 111.616B
256V = 157.44R - 131.84G - 25.6B
256R = 256Y + 291.84V
256G = 256Y - 99.84U - 148.48V
256B = 256Y + 519.68U
然后,我们就可以对上述公式进一步优化,彻底干掉小数,注意这里是有精度损失的。
256Y = 77R + 150G + 29B
256U = -38R - 74G + 112B
256V = 158R - 132G - 26B
256R = 256Y + 292V
256G = 256Y - 100U - 149V
256B = 256Y + 520U
实际上就是四舍五入,这是乘以256(即)是为了缩小误差,当然乘数越大,误差越小。
然后我们可以将等式左边的除到右边,同时将这个除法用位运算来代替,这样就获得了我们的第一个优化版代码,代码实现如下:
inline unsigned char ClampToByte(int Value) {
if (Value < 0)
return 0;
else if (Value > 255)
return 255;
else
return (unsigned char)Value;
//return ((Value | ((signed int)(255 - Value) >> 31)) & ~((signed int)Value >> 31));
}
void RGB2YUV_1(unsigned char *RGB, unsigned char *Y, unsigned char *U, unsigned char *V, int Width, int Height, int Stride)
{
const int Shift = 13;
const int HalfV = 1 << (Shift - 1);
const int Y_B_WT = 0.114f * (1 << Shift), Y_G_WT = 0.587f * (1 << Shift), Y_R_WT = (1 << Shift) - Y_B_WT - Y_G_WT;
const int U_B_WT = 0.436f * (1 << Shift), U_G_WT = -0.28886f * (1 << Shift), U_R_WT = -(U_B_WT + U_G_WT);
const int V_B_WT = -0.10001 * (1 << Shift), V_G_WT = -0.51499f * (1 << Shift), V_R_WT = -(V_B_WT + V_G_WT);
for (int YY = 0; YY < Height; YY++)
{
unsigned char *LinePS = RGB + YY * Stride;
unsigned char *LinePY = Y + YY * Width;
unsigned char *LinePU = U + YY * Width;
unsigned char *LinePV = V + YY * Width;
for (int XX = 0; XX < Width; XX++, LinePS += 3)
{
int Blue = LinePS[0], Green = LinePS[1], Red = LinePS[2];
LinePY[XX] = (Y_B_WT * Blue + Y_G_WT * Green + Y_R_WT * Red + HalfV) >> Shift;
LinePU[XX] = ((U_B_WT * Blue + U_G_WT * Green + U_R_WT * Red + HalfV) >> Shift) + 128;
LinePV[XX] = ((V_B_WT * Blue + V_G_WT * Green + V_R_WT * Red + HalfV) >> Shift) + 128;
}
}
}
void YUV2RGB_1(unsigned char *Y, unsigned char *U, unsigned char *V, unsigned char *RGB, int Width, int Height, int Stride)
{
const int Shift = 13;
const int HalfV = 1 << (Shift - 1);
const int B_Y_WT = 1 << Shift, B_U_WT = 2.03211f * (1 << Shift), B_V_WT = 0;
const int G_Y_WT = 1 << Shift, G_U_WT = -0.39465f * (1 << Shift), G_V_WT = -0.58060f * (1 << Shift);
const int R_Y_WT = 1 << Shift, R_U_WT = 0, R_V_WT = 1.13983 * (1 << Shift);
for (int YY = 0; YY < Height; YY++)
{
unsigned char *LinePD = RGB + YY * Stride;
unsigned char *LinePY = Y + YY * Width;
unsigned char *LinePU = U + YY * Width;
unsigned char *LinePV = V + YY * Width;
for (int XX = 0; XX < Width; XX++, LinePD += 3)
{
int YV = LinePY[XX], UV = LinePU[XX] - 128, VV = LinePV[XX] - 128;
LinePD[0] = ClampToByte(YV + ((B_U_WT * UV + HalfV) >> Shift));
LinePD[1] = ClampToByte(YV + ((G_U_WT * UV + G_V_WT * VV + HalfV) >> Shift));
LinePD[2] = ClampToByte(YV + ((R_V_WT * VV + HalfV) >> Shift));
}
}
}
需要注意的是这个代码和普通实现直接用浮点数计算的公式有些差别,因为普通实现里面应用的RGB和浮点数互转的公式是小数形式,即:。而我们这个版本里面使用的是整数形式,即:,而现在的公式变成了:
R= Y + ((360 * (V - 128))>>8) ;
G= Y - (( ( 88 * (U - 128) + 184 * (V - 128)) )>>8) ;
B= Y +((455 * (U - 128))>>8) ;
Y = (77*R + 150*G + 29*B)>>8;
U = ((-44*R - 87*G + 131*B)>>8) + 128;
V = ((131*R - 110*G - 21*B)>>8) + 128 ;
接下来各个版本的优化我们都以整数形式为例,并且这也是应用的最广泛的形式。
话不多说,我们来测一下速度:
| 分辨率 | 算法优化 | 循环次数 | 速度 |
|---|---|---|---|
| 4032x3024 | 普通实现 | 1000 | 150.58ms |
| 4032x3024 | 去掉浮点数,除法用位运算代替 | 1000 | 76.70ms |
不错,速度降了接近2倍。
5. RGB和YUV互转优化第二版
按照我们以前写文章的套路,第二版自然要来测一下OpenMP多线程,代码实现如下:
void RGB2YUV_OpenMP(unsigned char *RGB, unsigned char *Y, unsigned char *U, unsigned char *V, int Width, int Height, int Stride)
{
const int Shift = 8;
const int HalfV = 1 << (Shift - 1);
const int Y_B_WT = 0.114f * (1 << Shift), Y_G_WT = 0.587f * (1 << Shift), Y_R_WT = (1 << Shift) - Y_B_WT - Y_G_WT;
const int U_B_WT = 0.436f * (1 << Shift), U_G_WT = -0.28886f * (1 << Shift), U_R_WT = -(U_B_WT + U_G_WT);
const int V_B_WT = -0.10001 * (1 << Shift), V_G_WT = -0.51499f * (1 << Shift), V_R_WT = -(V_B_WT + V_G_WT);
for (int YY = 0; YY < Height; YY++)
{
unsigned char *LinePS = RGB + YY * Stride;
unsigned char *LinePY = Y + YY * Width;
unsigned char *LinePU = U + YY * Width;
unsigned char *LinePV = V + YY * Width;
#pragma omp parallel for num_threads(4)
for (int XX = 0; XX < Width; XX++)
{
int Blue = LinePS[XX*3 + 0], Green = LinePS[XX*3 + 1], Red = LinePS[XX*3 + 2];
LinePY[XX] = (Y_B_WT * Blue + Y_G_WT * Green + Y_R_WT * Red + HalfV) >> Shift;
LinePU[XX] = ((U_B_WT * Blue + U_G_WT * Green + U_R_WT * Red + HalfV) >> Shift) + 128;
LinePV[XX] = ((V_B_WT * Blue + V_G_WT * Green + V_R_WT * Red + HalfV) >> Shift) + 128;
}
}
}
void YUV2RGB_OpenMP(unsigned char *Y, unsigned char *U, unsigned char *V, unsigned char *RGB, int Width, int Height, int Stride)
{
const int Shift = 8;
const int HalfV = 1 << (Shift - 1);
const int B_Y_WT = 1 << Shift, B_U_WT = 2.03211f * (1 << Shift), B_V_WT = 0;
const int G_Y_WT = 1 << Shift, G_U_WT = -0.39465f * (1 << Shift), G_V_WT = -0.58060f * (1 << Shift);
const int R_Y_WT = 1 << Shift, R_U_WT = 0, R_V_WT = 1.13983 * (1 << Shift);
for (int YY = 0; YY < Height; YY++)
{
unsigned char *LinePD = RGB + YY * Stride;
unsigned char *LinePY = Y + YY * Width;
unsigned char *LinePU = U + YY * Width;
unsigned char *LinePV = V + YY * Width;
#pragma omp parallel for num_threads(4)
for (int XX = 0; XX < Width; XX++)
{
int YV = LinePY[XX], UV = LinePU[XX] - 128, VV = LinePV[XX] - 128;
LinePD[XX*3 + 0] = ClampToByte(YV + ((B_U_WT * UV + HalfV) >> Shift));
LinePD[XX*3 + 1] = ClampToByte(YV + ((G_U_WT * UV + G_V_WT * VV + HalfV) >> Shift));
LinePD[XX*3 + 2] = ClampToByte(YV + ((R_V_WT * VV + HalfV) >> Shift));
}
}
}
测一下速度:
| 分辨率 | 算法优化 | 循环次数 | 速度 |
|---|---|---|---|
| 4032x3024 | 普通实现 | 1000 | 150.58ms |
| 4032x3024 | 去掉浮点数,除法用位运算代替 | 1000 | 76.70ms |
| 4032x3024 | OpenMP 4线程 | 1000 | 50.48ms |
6. RGB和YUV互转优化第三版
接下来我们将上面的代码用SSE指令集来做一下优化,代码如下:
https://github.com/BBuf/Image-processing-algorithm-Speed/blob/master/speed_rgb2yuv_sse.cpp#L450
https://github.com/BBuf/Image-processing-algorithm-Speed/blob/master/speed_rgb2yuv_sse.cpp#L339
这个代码比较简单,就不做过多解释了,因为我在【AI PC端算法优化】二,一步步优化自然饱和度算法述 这篇文章里已经仔细讲解了如何将BGR的内存排布方式拆成B,G,R分别连续的内存排列方式,如果你想进一步了解请点击上面链接。剩下的就是将第四节的代码直接使用SSE指令集向量化了。我们来看一下速度测试:
| 分辨率 | 算法优化 | 循环次数 | 速度 |
|---|---|---|---|
| 4032x3024 | 普通实现 | 1000 | 150.58ms |
| 4032x3024 | 去掉浮点数,除法用位运算代替 | 1000 | 76.70ms |
| 4032x3024 | OpenMP 4线程 | 1000 | 50.48ms |
| 4032x3024 | 普通SSE向量化 | 1000 | 48.92ms |
可以看到,它的速度和OpenMP4线程持平,好气啊,如果就这样就结束了,不符合我的风格啊,继续探索是否有其它可以优化的地方。
7. RGB和YUV互转优化第四版
从ImageShop大佬博主这里发现一个Idea,那就是继续考虑是否可以通过减少指令的个数来获得加速呢?
我们知道在SSE中有一个指令集为_mm_madd_epi16,它实现的功能为:
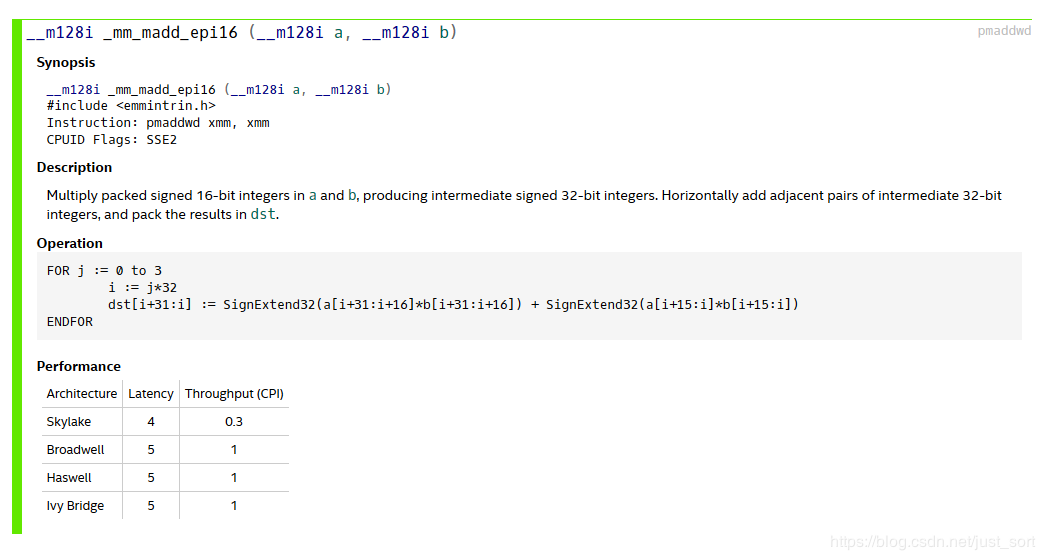
更形象的表示为:
r0 := (a0 * b0) + (a1 * b1)
r1 := (a2 * b2) + (a3 * b3)
r2 := (a4 * b4) + (a5 * b5)
r3 := (a6 * b6) + (a7 * b7)
即这个指令集完成了两个SSE向量的相互乘加,如果我们可以用这个指令去代替我们上一版SSE优化中的疯狂加和操作,速度会有提升?
接下来我们就一起验证一下,首先我们来看一下原始的转换公式:
LinePY[XX] = (Y_B_WT * Blue + Y_G_WT * Green + Y_R_WT * Red + HalfV) >> Shift;
LinePU[XX] = ((U_B_WT * Blue + U_G_WT * Green + U_R_WT * Red + HalfV) >> Shift) + 128;
LinePV[XX] = ((V_B_WT * Blue + V_G_WT * Green + V_R_WT * Red + HalfV) >> Shift) + 128;
注意到其中的HalfV=1<<(Shift-1),我们得到:
LinePY[XX] = (Y_B_WT * Blue + Y_G_WT * Green + Y_R_WT * Red + 1 * HalfV) >> Shift;
LinePU[XX] = (U_B_WT * Blue + U_G_WT * Green + U_R_WT * Red + 257 * HalfV) >> Shift;
LinePV[XX] = (V_B_WT * Blue + V_G_WT * Green + V_R_WT * Red + 257 * HalfV) >> Shift;
通过这样变形,我们就可以只用个_mm_madd_epi16指令就可以代替之前的大量乘加指令。另外,这里再看一下指令集的描述,Multiply packed signed 16-bit integers in a and b, producing intermediate signed 32-bit integers. Horizontally add adjacent pairs of intermediate 32-bit integers, and pack the results in dst. 即参与计算的数必须是有符号的位数据,首先图像数范围[0,255],肯定满足要求,同时注意到上述系数绝对值都小于1,因此只要(1 << Shift)不大于32768,即Shift最大取值15是能够满足需求的,由于下面YUV2RGB有点特殊,只能取到13,这里为了保持一致,在RGB2YUV的过程也把Shift取成了13。
这里比较难实现的一个地方在于这里使用_mm_madd_epi16这里的系数是交叉的,比如我们变量b里面保存了交叉的B和G分量的权重,那么变量a就保存了Blue和Green的像素值,这里有个实现方法:1、我们上述代码里已经获得了Blue和Green分量的连续排列变量,这个时候只需要使用unpacklo和unpackhi就能分别获取低8位和高8位的交叉结果。2、注意到获取Blue和Green分量的连续排列变量时是用的shuffle指令,我们也可以采用不同的shuffle系数直接获取交叉后的结果。
这里采用了第二种方法,速度比较快。
代码实现如下:
https://github.com/BBuf/Image-processing-algorithm-Speed/blob/master/speed_rgb2yuv_sse.cpp#L339
https://github.com/BBuf/Image-processing-algorithm-Speed/blob/master/speed_rgb2yuv_sse.cpp#L450
这里需要注意一下,在YUV2BGR的SSE实现的时候,以LinePD[0]为例子:
LinePD[0] = ClampToByte(YV + ((B_U_WT * UV + HalfV) >> Shift))
展开:
LinePD[0] = ClampToByte(YV * (1 << Shift) + B_U_WT * UV + (1 << (Shift - 1))) >> Shift))
= ClampToByte((YV + 0.5) * (1 << Shift) + B_U_WT * UV) >> Shift))
= ClampToByte((YV * 2 + 1) * ((1 << Shift) >> 1) + B_U_WT * UV) >> Shift))
上面提到Shift最大只能取13,是因为这里LinePD[0]的转换里面有个系数2.03>2,为了不数据溢出,只能取13了。这里的实现方法和RGB2YUV的SSE高级优化是一致的,这一部分我就不提供源码了。在ImageShop的博客中还看到一个想法就是,在复现论文或者实际工程中我们一般只会处理Y通道的数据,我们没有必要关注和转换U,V通道的数据,这样我们可以把整个算法处理得更快。
再来测一把速度,会不会翻车呢?
| 分辨率 | 算法优化 | 循环次数 | 速度 |
|---|---|---|---|
| 4032x3024 | 普通实现 | 1000 | 150.58ms |
| 4032x3024 | 去掉浮点数,除法用位运算代替 | 1000 | 76.70ms |
| 4032x3024 | OpenMP 4线程 | 1000 | 50.48ms |
| 4032x3024 | 普通SSE向量化 | 1000 | 48.92ms |
| 4032x3024 | _mm_madd_epi16二次优化 | 1000 | 33.04ms |
速度还是快了不少的,相对于我们的初始实现现在已经有5倍左右的加速了。
8. RGB和YUV互转优化第五版
刚才开启OpenMP 4线程的速度都快赶上SSE第一版优化的速度了,这提醒了我是不是可以将多线程应用在SSE上进一步加速呢?来试试。按照之前的思路,std::async+上一节的SSE代码,实现如下:
https://github.com/BBuf/Image-processing-algorithm-Speed/blob/master/speed_rgb2yuv_sse.cpp#L757
https://github.com/BBuf/Image-processing-algorithm-Speed/blob/master/speed_rgb2yuv_sse.cpp#L771
注意,我这里实现的其实仍然是高方向的线程,因为我的笔记本只有个核心,所以static_cast<int32_t>(std::thread::hardware_concurrency())=4,或许你想问在宽方向继续多线程可以提速吗?我是不知道的,我正在探索,有结论发文章说说。
来测一下速度。
| 分辨率 | 算法优化 | 循环次数 | 速度 |
|---|---|---|---|
| 4032x3024 | 普通实现 | 1000 | 150.58ms |
| 4032x3024 | 去掉浮点数,除法用位运算代替 | 1000 | 76.70ms |
| 4032x3024 | OpenMP 4线程 | 1000 | 50.48ms |
| 4032x3024 | 普通SSE向量化 | 1000 | 48.92ms |
| 4032x3024 | _mm_madd_epi16二次优化 | 1000 | 33.04ms |
| 4032x3024 | SSE+4线程 | 1000 | 23.70ms |
可以看到,速度进一步优化了,现在变成了23.7ms。
9. 总结
基本上还是我以前的那些套路,总的来说相比于原始实现的速度,快了倍,关于进一步加速的想法我感觉大概得从宽方向上的多线程以及尝试AVX2指令集等吧。。有问题欢迎在留言区讨论。
10. 参考
https://www.cnblogs.com/Imageshop/p/8405517.html