清华大学朱军:贝叶斯学习回顾与最新进展
编者荐语:
6月6日,中国计算机学会(CCF)主办的中国计算机学会青年精英大会(CCF YEF)在线上举行,其中,朱军教授做了题为《贝叶斯学习回顾与展望》报告,总时长为1个小时左右,内容主要分为五个部分:贝叶斯理论应对不确定性、贝叶斯理论和经典算法等。
以下文章来源于AI科技评论 ,作者蒋宝尚
AI科技评论
点评学术,服务 AI !

贝叶斯应对不确定性

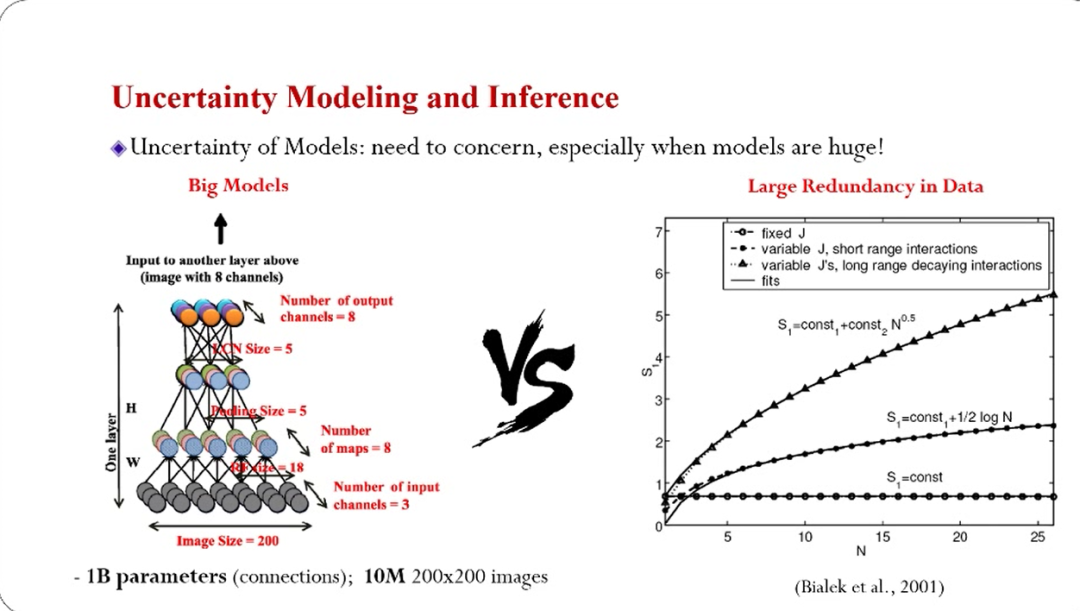
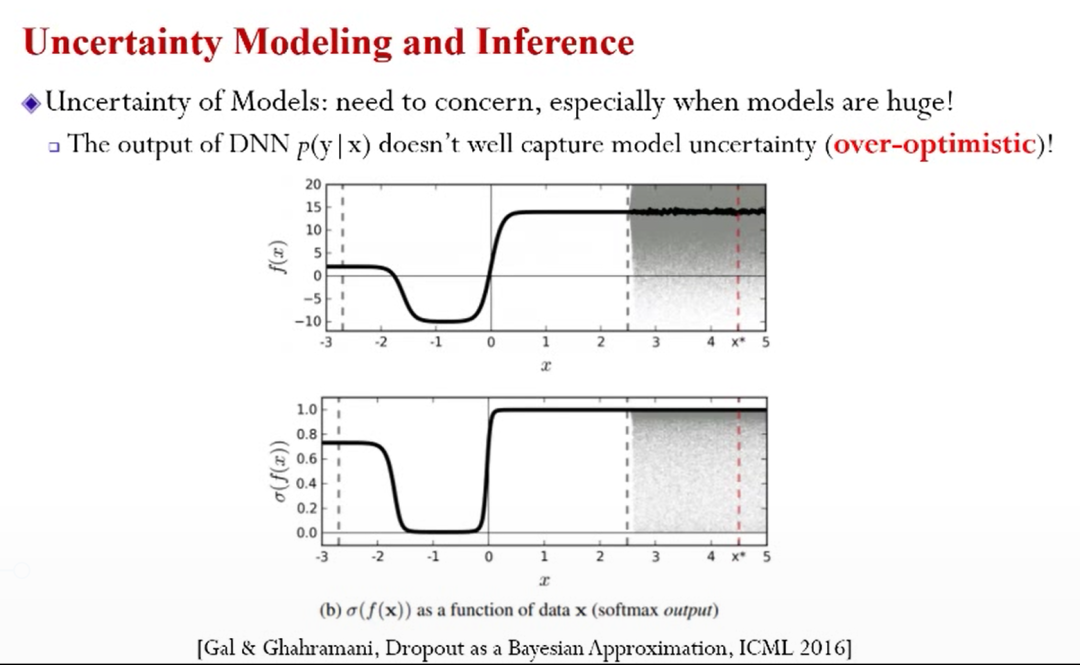
贝叶斯理论

经典的贝叶斯方法

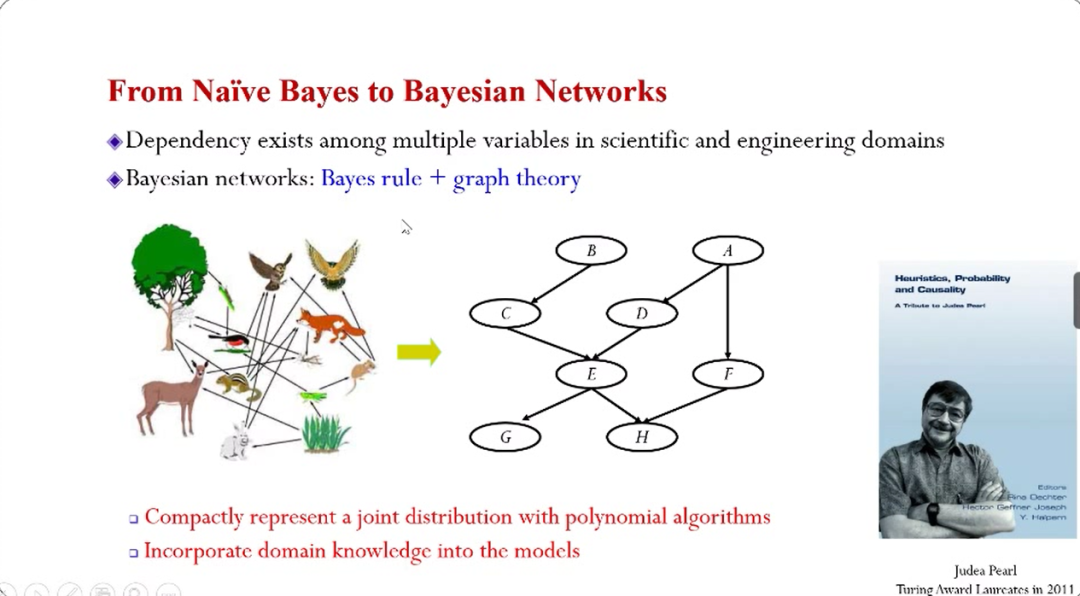
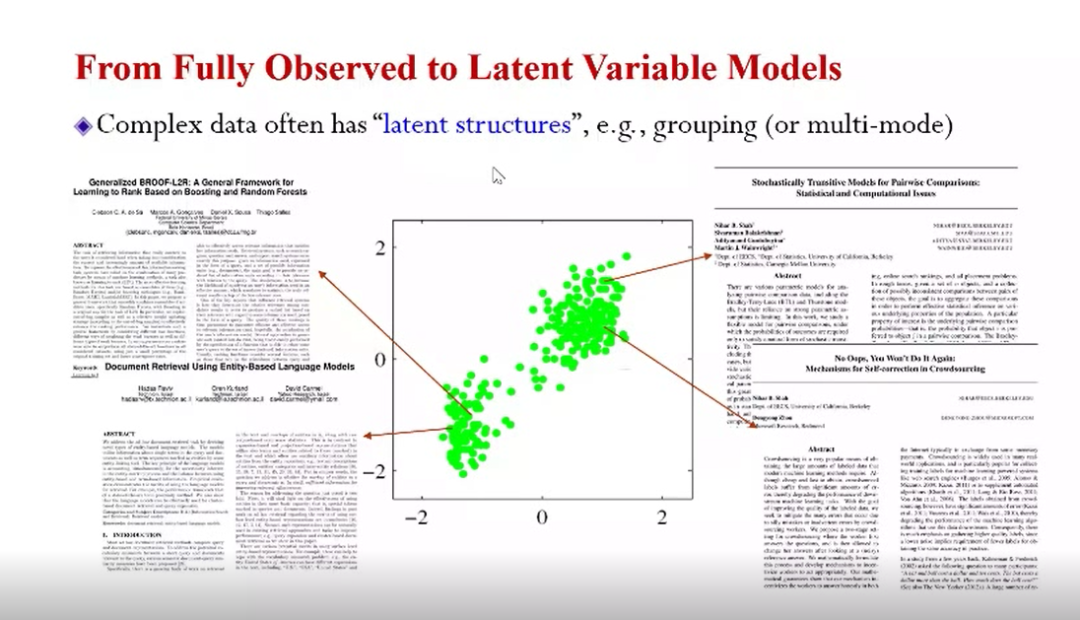

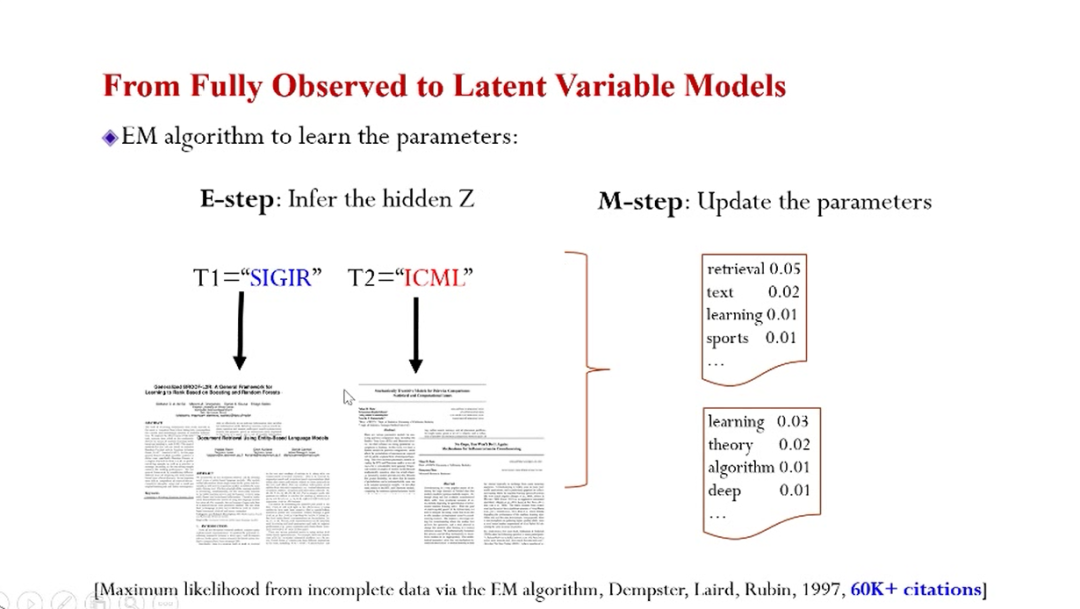
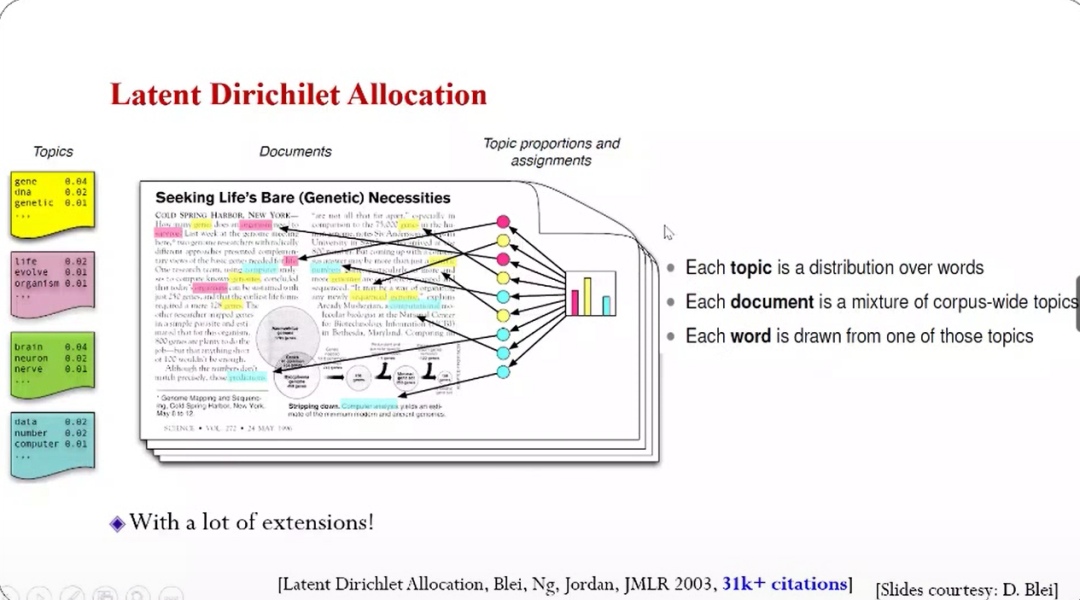

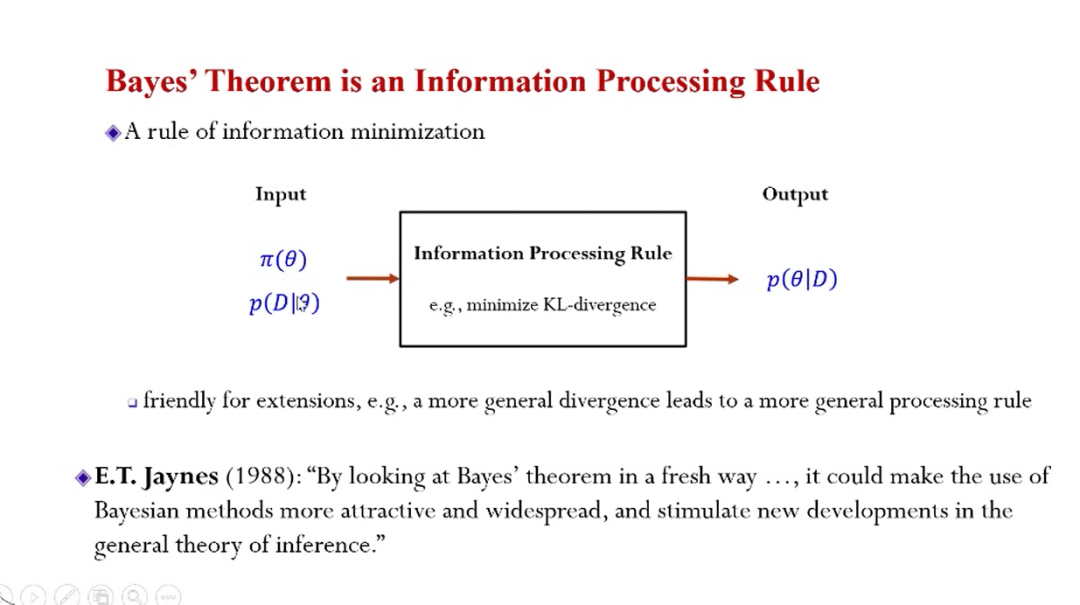

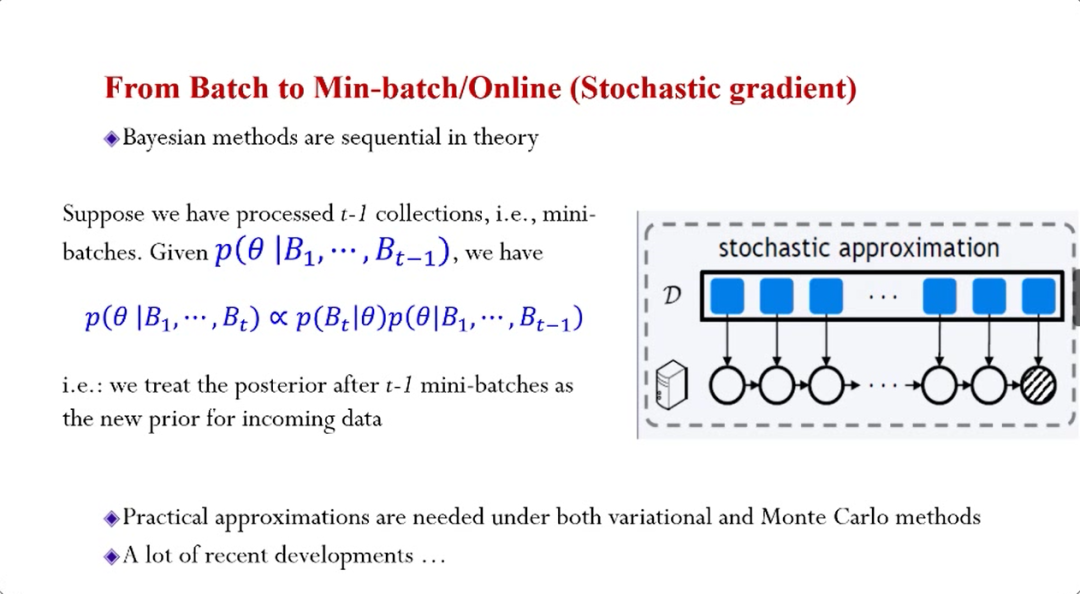
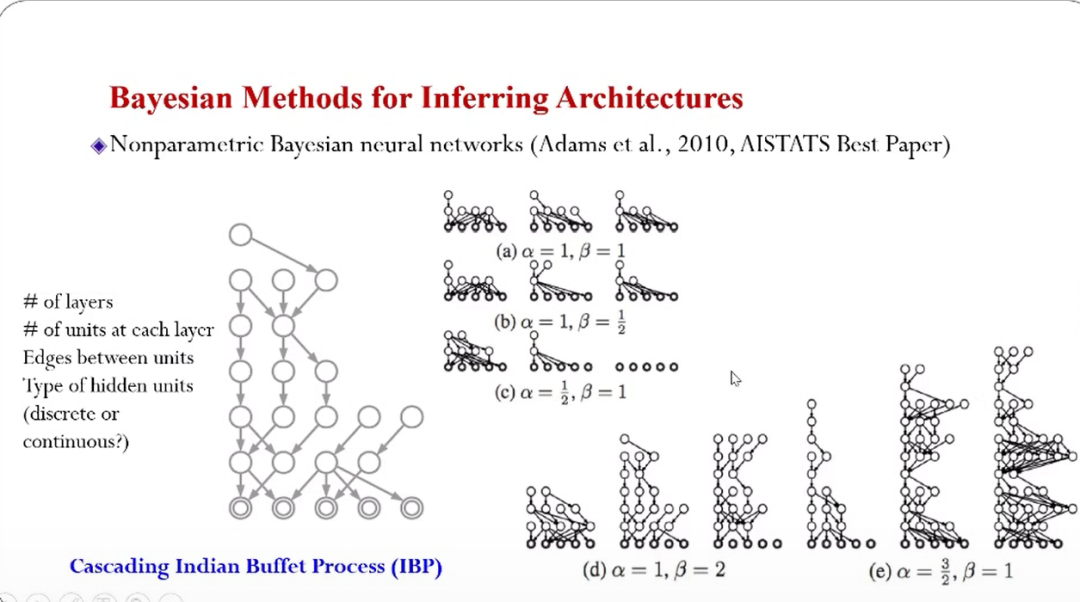
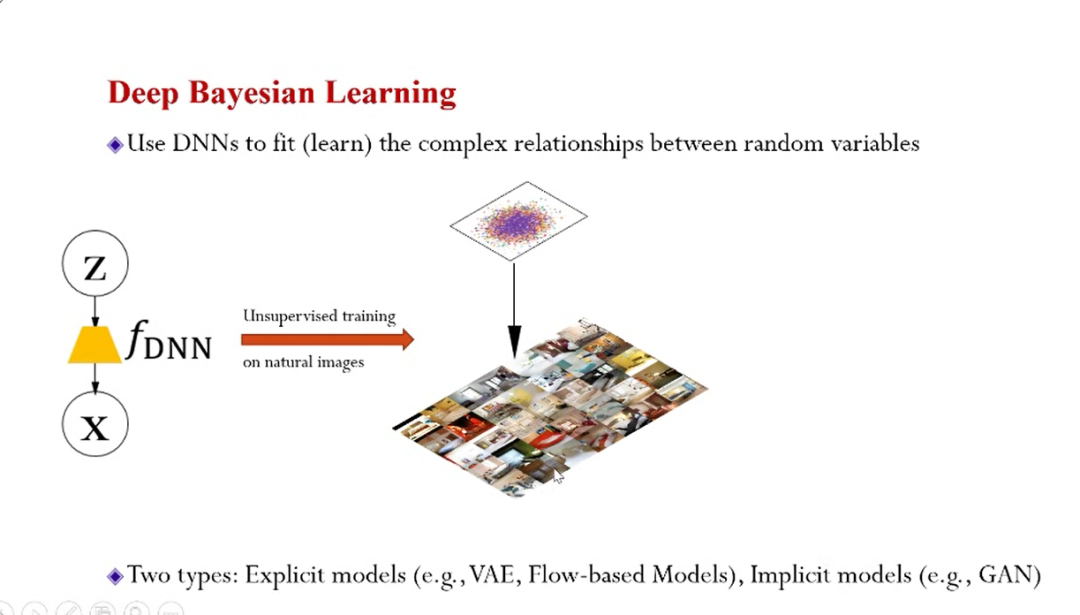
可扩展贝叶斯机器学习
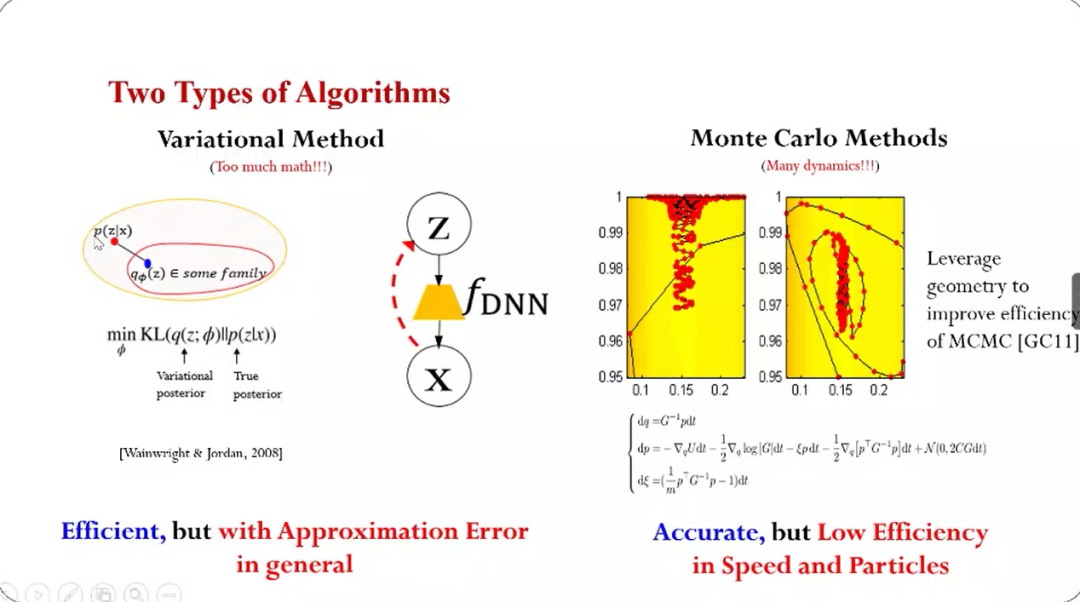


怎么去编程——珠算


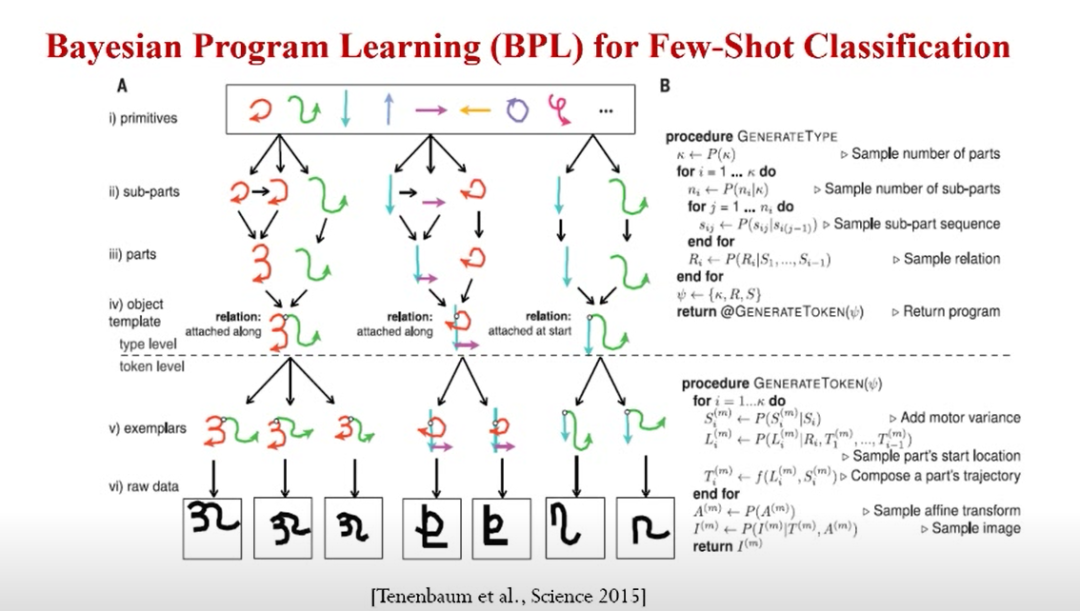
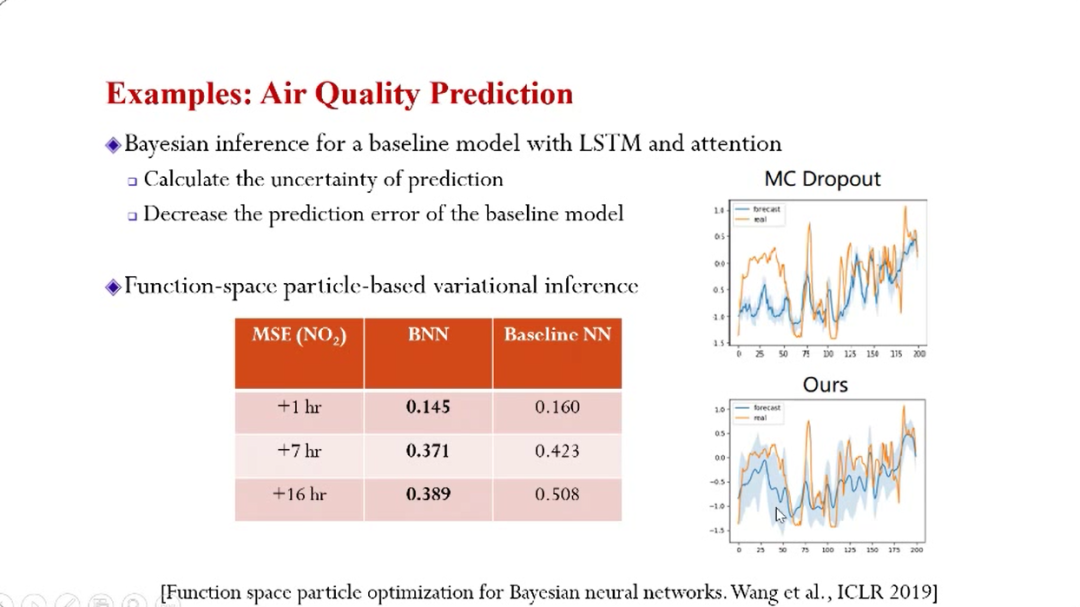
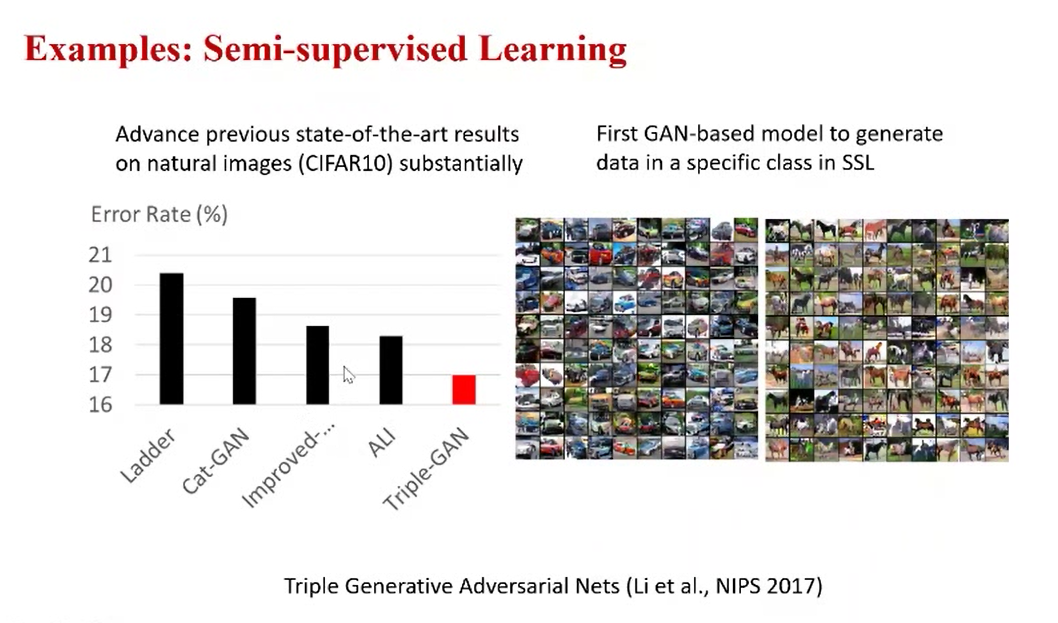
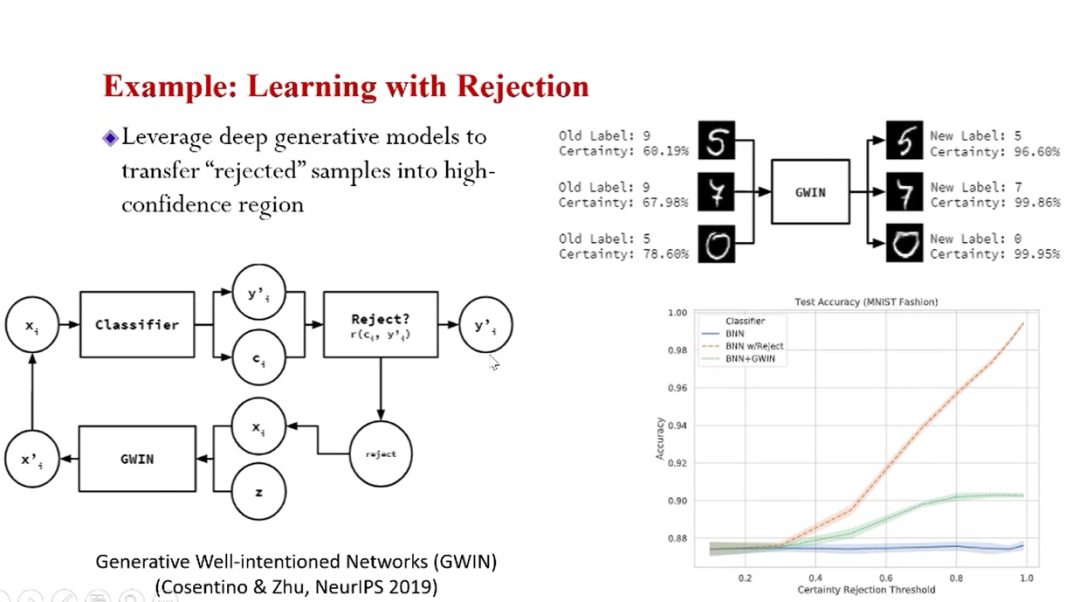
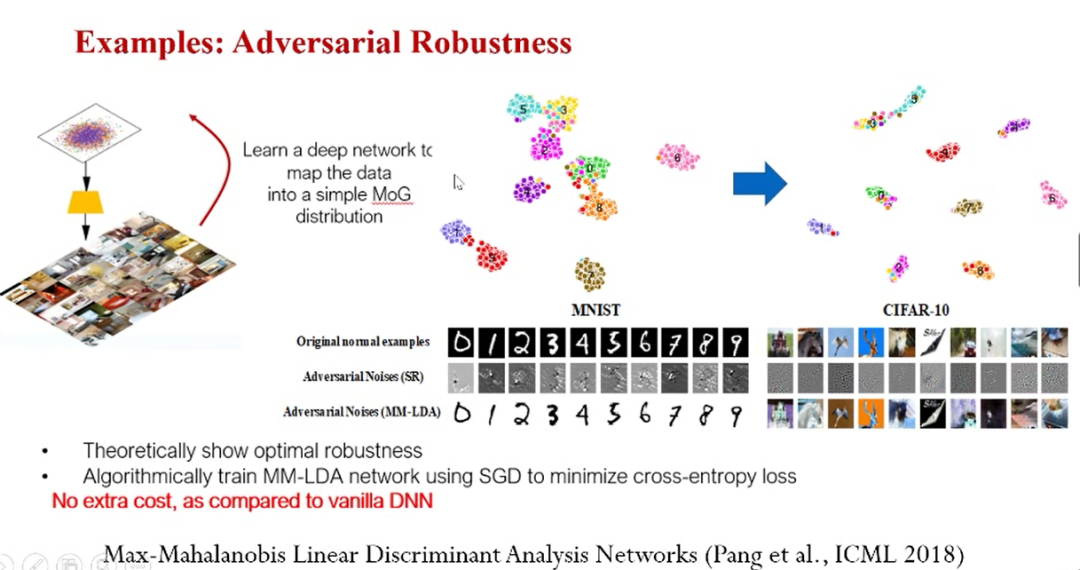
贝叶斯建模的应用例子
往期回顾



