学做锅包肉与学信号处理有关系吗?有吗?没有吗?

你很好引
把你引进去
自我们人类有史以来,信号就是时刻伴随着我们的。
比如在远古时代,古人们之间还没有语言,他们对彼此做的各种手势、各种肢体动作都是信号,其中包含着想要表达的信息,比如小心野兽、撤回营地等等。
到了后来,人类开始有了自己的语言,语言的出现使人类的文明程度上升到了一个新的高度,因为我们开始注重对信息的处理,并不断地加强对信息的处理,开始追求统一化、标准化。
这里必须明确信号与信息的区别:信号是运载信息的载体,没有信息,信号将毫无意义;而信息则是知识等用于交流的消息抽象代名词,没有载体运载信息、信息也将毫无意义。可以说信号与信息既是完全不同的两个概念,又是密不可分的。
可以说语言催动了“电话”的诞生,而在电话出现之前,首先出现的是用于军事方面的通信系统:1793年,法国查佩兄弟俩在巴黎和里尔之间架设了一条230千米长的接力方式传送信息的托架式线路。这是一种由16个信号塔组成的通信系统。信号机由信号员在下边通过绳子和滑轮,操纵支架的不同角度,表示相关的信息。当时,法国和奥地利正在作战,信号系统只用一个小时就把从奥军手中夺取埃斯河畔孔代的胜利消息传到巴黎。
20世纪60年代中期高速数字计算机的诞生将人类的信号与信息处理能力带入了一个空前的水平。人类也进入“信息时代”。由法国数学家傅里叶提出的傅立叶变换、以及衍生出各种变换,到现在的快速傅立叶变换等等开始广泛地被应用到各种利用计算机处理的信息中,高速计算机和这些算法的结合,开启了信号与信息处理的一个崭新时代。
今天我们就来从做锅包肉的角度理解一下傅里叶变换。

如何理解傅里叶变换
请看下图:他显示的信号有四个频率分量:分别是5,10,20,50Hz。
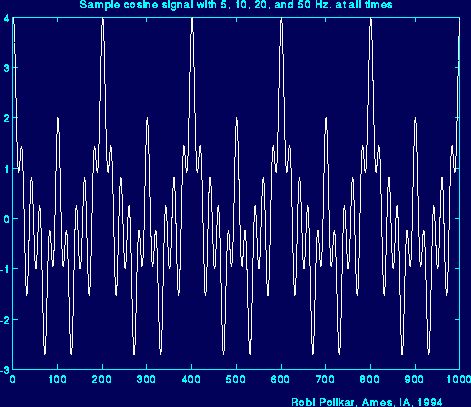

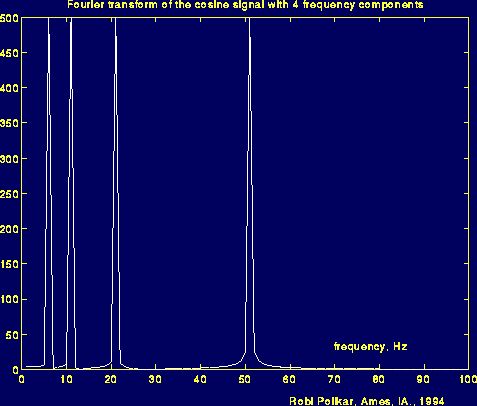
从某种程度上讲,可以说傅里叶变换是振动诊断的基础,也可以说正是有了它才有了现在的故障诊断这个学科。

即生“傅里叶变换”何生“小波”?
乍一看我好像是会做锅包肉了,但是实际则不然,因为我不知道这些食材烹饪的顺序。“傅大厨”我火都开了,你就跟我说这些,不够啊!
这就好像是下图这个意思,我是混合信号,还是先低频信号再高频,亦或者是先高频信号再低频,傅里叶变化之后都是差不多的。
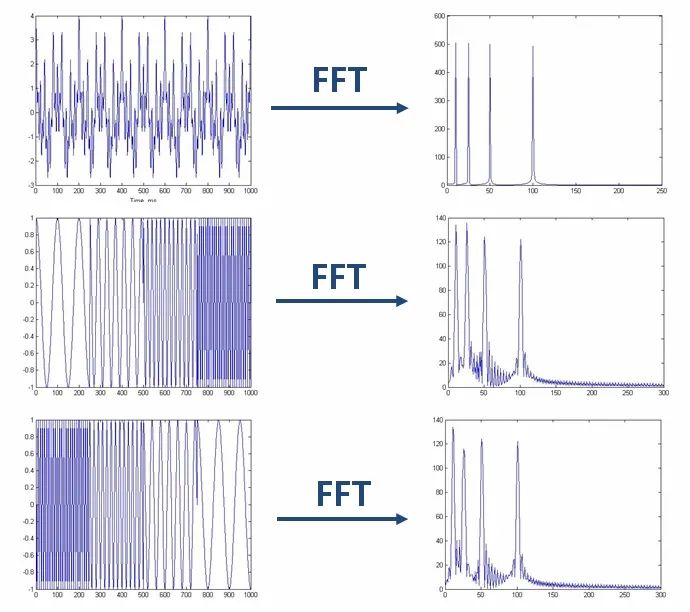
也就是说“傅大厨的宝典”处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。

当我倒掉一锅热油时的小眼神就像是失忆的尔康
所以想完全复制出一盘锅包肉,我们还要分析出食材加入的时间点。就像是我们处理上面那三个信号,要知道各个频率的时间点。因此就有了小波分析。
从下面的动图我们可以观察出来,傅里叶变换的函数基都是三角函数,而三角函数可以看作是一个“大波”。
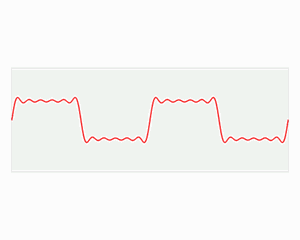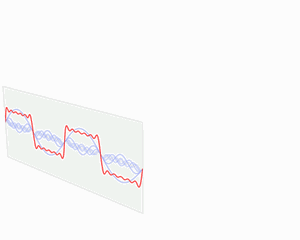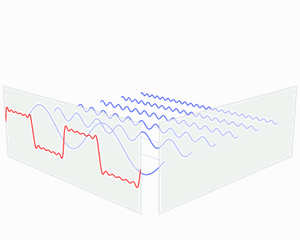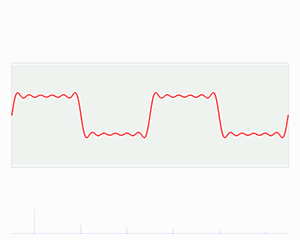
那小波为什么能解决问题呢?是因为小波变换将傅里叶变换中无限长的三角函数基换成了有限长的会衰减的小波基。
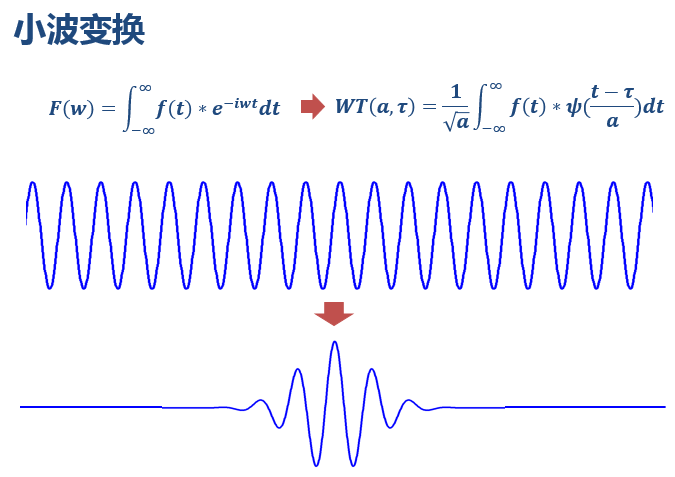
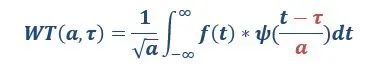
从小波的公式可以看出,它有两个变量(“傅大厨”的只有一个频率分量):尺度a(scale)和平移量t(translation)。尺度a控制小波函数的伸缩,平移量控制小波函数的平移。尺度就对应于频率(反比),平移量t就对应于时间。
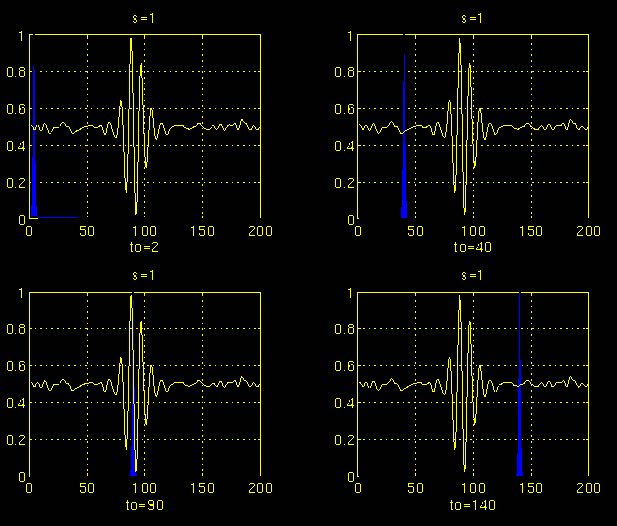
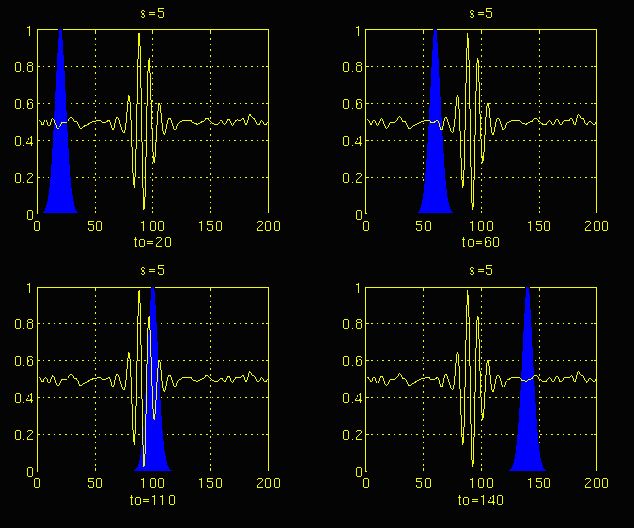
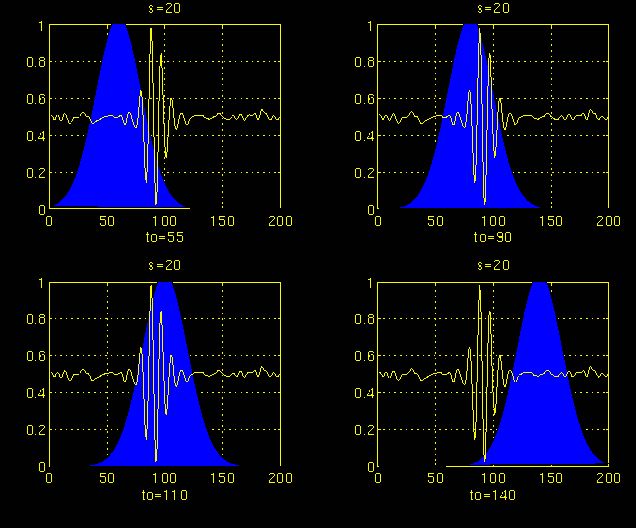
在此过程中,选取母小波作为所有窗口的原型。所有使用的窗口都是放大(或压缩)和移动的母小波。为了方便起见,从尺度s = 1开始,分析将从高频开始,向低频进行。s的第一个值对应的是压缩幅度最大的小波。随着s值的增大,小波会膨胀。小波被放置在信号的开始点对应于的时间。
这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。
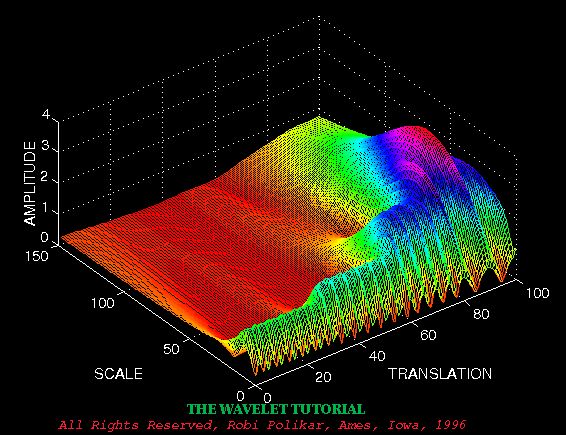
上图为信号的连续小波变换结果。值得注意的是坐标轴是平移和缩放,而不是时间和频率。然而,平移与时间是严格相关的,因为它表明了母小波的位置。母小波的平移可以被认为是时间流逝。
本着学习信号处理的思路,今天小编终于学会了做锅包肉,一家人也愉快的生活在了一起。

参考资料:
【互动问题:你对做菜和处理信号之间的学问有什么要说的吗?】
请大家按照 互动:问题答案 的格式在评论区留言参与互动。
截止到下周某下午2点,点赞数前三名的朋友将获得我们送出的礼物。
疫情过后我们将更换精美礼品,并将礼品将尽快送至您手上。
上期获奖留言截图



在此我们感谢读者发来的礼物秀!
编辑|须臾
