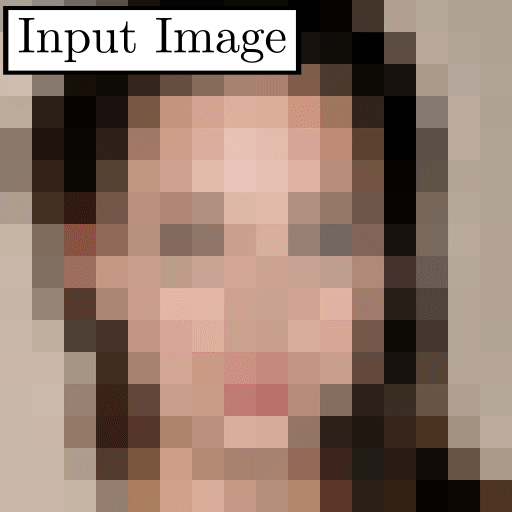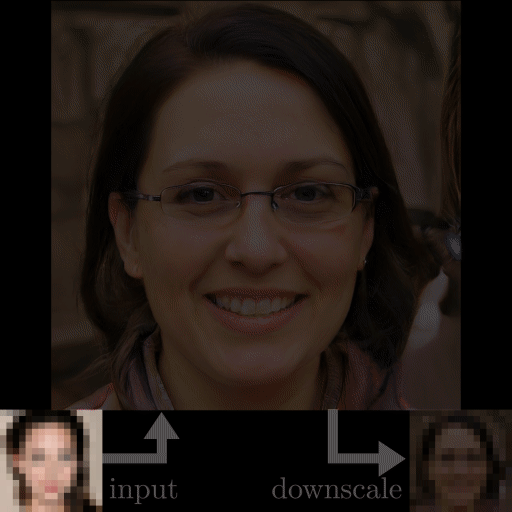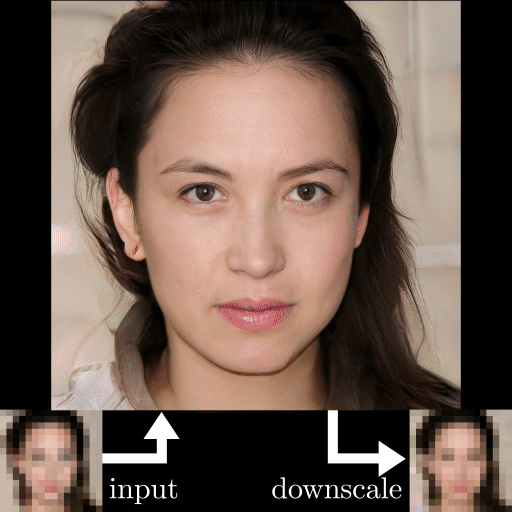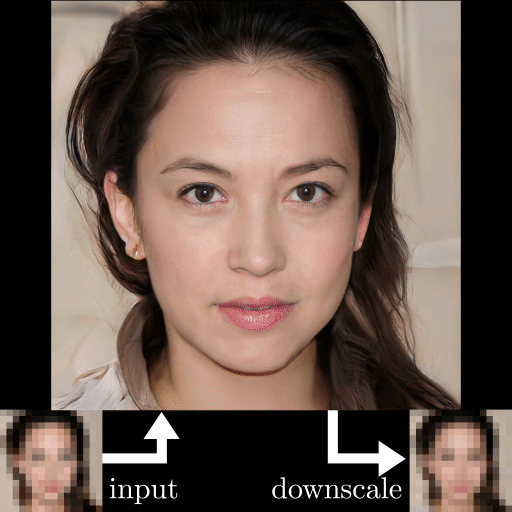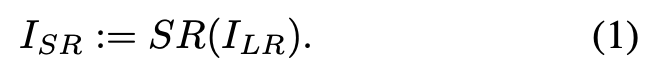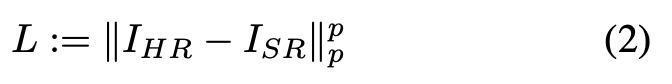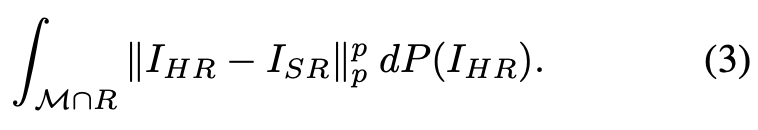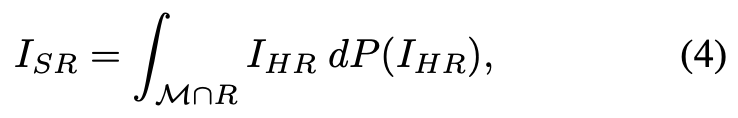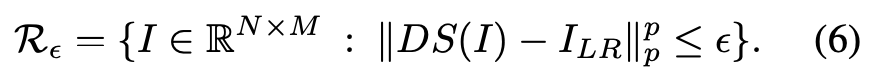全世界有3.14 % 的人已经关注了
爆炸吧知识
来源:机器之心
参与:魔王、杜伟
有了这个工具,我们终于能够看到马赛克下的那张脸了。
杜克大学近期的一项研究可以将高糊人脸照片转换成清晰的面部图像,而且你完全看不出来图像中的人并非真人,而是计算机生成的人脸。此外,这个名为 PULSE 的方法还可以「有来有往」,生成的高分辨率照片可以再次降级,回到高糊状态。在具体实现方面,该方法使用了 StyleGAN 来生成高分辨率图像。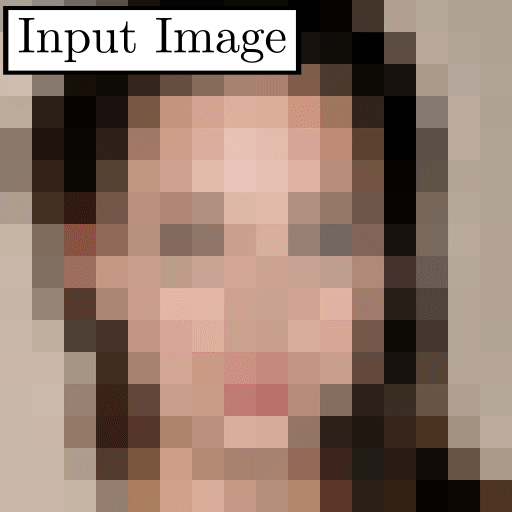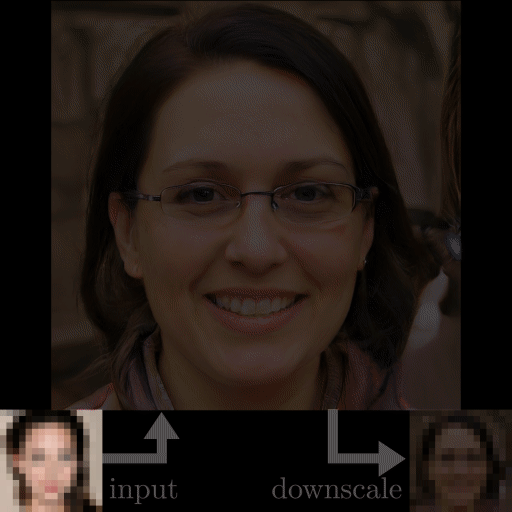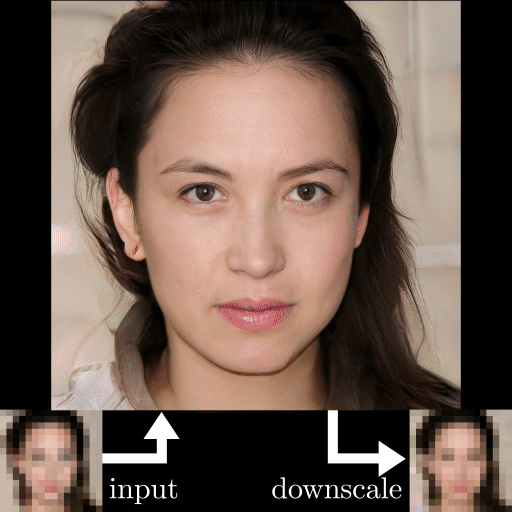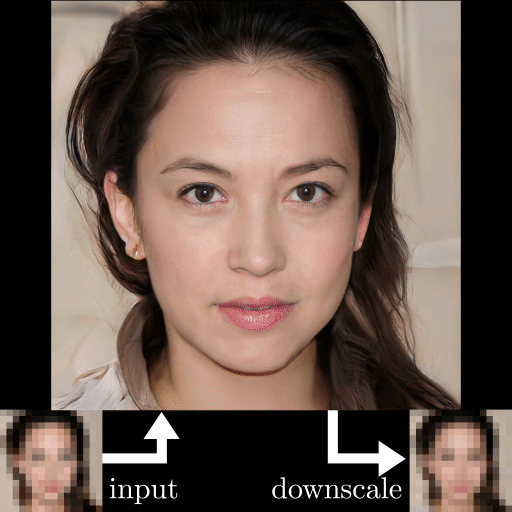
看起来,PULSE 方法与其他方法相比,展示出了更好的生成效果,清晰度更高,细节也更加丰富。
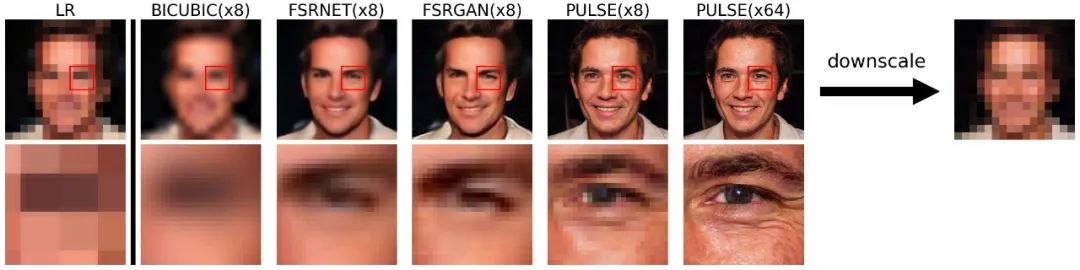
不过,AI 方法「看到」的面部图像和我们猜测的似乎存在差别。该项目提供了 Colab 环境,众多网友试用后发现了一些效果不太好的例子。
奥巴马似乎变年轻了,好像也变白了,但这还是奥巴马吗?


有网友质疑该方法生成结果存在偏见,尤其是对黑人图像的处理效果并不好。对此,项目作者给出了回应:PULSE 生成白人面部图像的频率确实要高于有色人种的面部图像。这一偏见很可能来自于 StyleGAN 的训练数据集,可能还有其他未知因素。我们意识到偏见是机器学习和计算机视觉领域的重要问题,并就此问题联系了 StyleGAN 和 FFHQ 数据集的创建者。我们希望这能够促进不具备此类偏见行为的方法的诞生。
此外,PULSE 作者强调,该方法最后输出的高分辨率图像并非真人。因此,该方法无法用于识别或重建原始图像,大家无需担心该方法会对现实中的人造成困扰。论文地址:https://arxiv.org/abs/2003.03808
GitHub 地址:https://github.com/adamian98/pulse
网站地址:http://pulse.cs.duke.edu/
Colab 地址:https://colab.research.google.com/github/tg-bomze/Face-Depixelizer/blob/master/Face_Depixelizer_Eng.ipynb
单图像超分辨率任务即基于低分辨率(LR)输入生成高分辨率(HR)图像。之前的方法通常是监督式的,其训练目标通常是度量超分辨率(SR)和高分辨率图像之间的像素级平均距离。而对此类度量指标的优化往往导致模糊,尤其是高方差区域的模糊。杜克大学将超分辨率问题重构为:如何创建可以准确降级回去的逼真 SR 图像。这提供了图像超分辨率的新范式。具体来说,研究者提出一种新型超分辨率算法 PULSE (Photo Upsampling via Latent Space Exploration),该算法可以生成高分辨率的逼真图像,分辨率之高超过之前的方法。此外,PULSE 是以完全自监督的方式进行的,且不受限于训练期间使用的特定降级算子(degradation operator),这与之前的方法有所不同。PULSE 不从 LR 图像开始缓慢地添加细节,而是遍历高分辨率自然图像流形,搜索可以降级至原始 LR 图像的高分辨率图像。这一过程通过「降尺度损失」(downscaling loss)完成,它指引着在生成模型潜在空间中的探索。此外,研究者利用高维高斯的特性限制搜索空间,使其保证输出结果是逼真的。因此,PULSE 得以生成既逼真又能进行恰当分辨率降级的超分辨率图像。该研究进行了大量实验,表明 PULSE 方法在人脸超分辨率领域中的效果。该方法以更高的分辨率和缩放因子(scale factor)超过了当前最优方法的感知质量。具体而言,PULSE 可以在几秒钟内将 16x16 像素图像转换为 1024 x 1024 像素图像,添加了一百万像素。此外,它还可以将低分辨率图像中无法看清的毛孔、皱纹、头发等转换得清晰。研究者请 40 个人对 PULSE 和其他五种方法生成的 1440 张图像进行评分(1-5 分),结果表明 PULSE 分数最高,接近真人的高质量图像。研究者首先定义了超分辨率问题的术语。假设低分辨率图像为 I_LR,超分辨率方法即学习一个条件生成函数 G,把 G 应用于 I_LR 时可以得到超分辨率图像 I_SR。形式上,I_LR ∈ R^m×n。期望函数 SR 是 R^m×n → R^M×N 的映射(M > m, N > n)。于是超分辨率图像 I_SR ∈ R^M×N 可被定义为: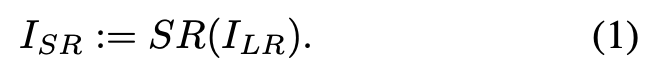
传统的超分辨率方法认为,低分辨率图像可以表示与理论上高分辨率图像 I_HR ∈ R^M×N 相同的信息。然后此类方法试图基于 I_LR 恢复特定 I_HR,从而将超分辨率问题简化为优化任务:拟合函数 SR,使下式最小化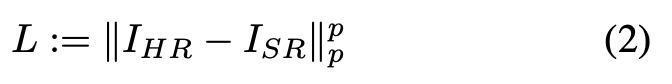
然而,在实践中,即使得到了正确的训练,这些算法仍无法提升高方差区域的细节。让我们通过修复低分辨率图像 I_LR,来探究其背后的原因。假设 M 是 R^M×N 中的自然图像流形,即 R^M×N 的这一子集类似自然逼真图像;假设 P 是基于 M 的概率分布,用于描述数据集中某张图像出现的概率;假设 R 是分辨率恰当降低后的图像集合,即 R = {I ∈ R^N×M : DS(I) = I_LR}。则随着数据集规模趋向于无穷大,算法输出修复图像 I_SR 的期望损失是: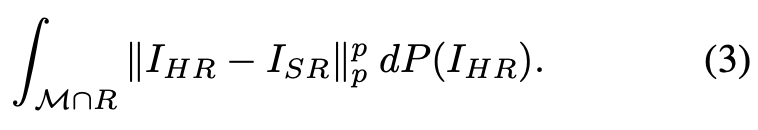
当 I_SR 是 I_HR(M ∩ R)的 l_p 平均时,损失得到最小化。事实上,当 p = 2 时,损失最小化,即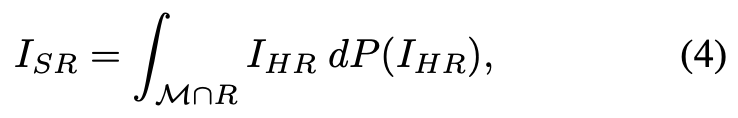
因此,最优 I_SR 是分辨率恰当降低的高分辨率图像集合的像素级加权平均值。因此,这些算法缺乏细节仅仅是因为无法通过改变网络架构来恢复 l_p 范数。杜克大学对该问题进行了重新定义,他们提出一种新型单图像超分辨率框架。对于 LR 图像 I_LR ∈ R^m×n 且 ϵ > 0,杜克大学研究者旨在找到符合下列条件的图像 I_SR ∈ M: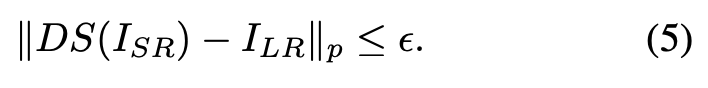
具体而言,令 R_ϵ ⊂ R^N×M 表示分辨率恰当降低的图像集合,即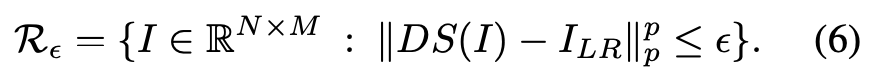
然后寻找图像 ISR ∈ M∩R_ϵ。M∩ R_ϵ 是可行解的集合,因为如果得到解的分辨率无法恰当降低或者不够逼真,则它并非可行解。有趣的是,M∩R_ϵ的交集(尤其是 M ∩ R_0) 不能为空,因为它们必须包含原始高分辨率图像(即传统方法旨在重建的图像)。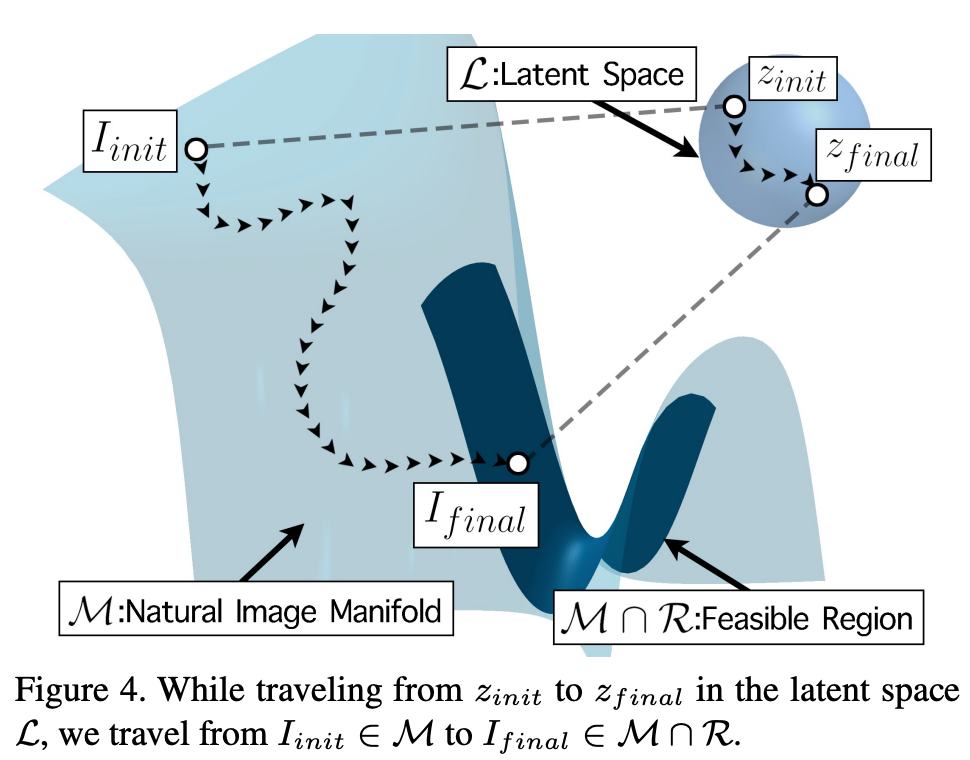
研究者通过多项实验对该算法进行评估,并将重点放在了人脸幻觉(face hallucination)这一热点问题上。具体来说,研究者利用了 Karras 等人在 Flickr Face HQ (FFHQ) 数据集上预训练的 Face StyleGAN。对于每个实验,他们从随机初始化开始,进行了 100 次学习率为 0.4 的球面梯度下降迭代。因此,该方法使用单个英伟达 V100 GPU 生成每张图像的时间约为 5 秒。
图 5:PULSE 与双三次升尺度(bicubic upscaling)、FSRNet 和 FSRGAN 方法的效果对比。在第一张图像中,PULSE 在头发里添加了一个 messy 图像块,以匹配 LR 图像放大后中间可见的两个黑色对角线像素值。研究者进行了感知超分辨率文献中常用的 MOS 分数评估,如下表所示: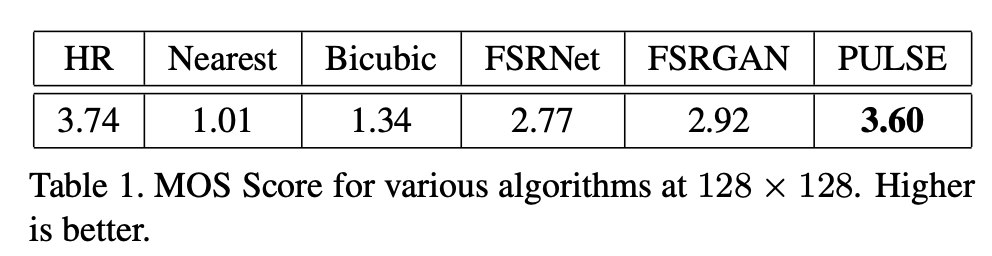
表 1:PULSE 与其他几种方法在 128×128 分辨率上的 MOS 分数,其中分数越高效果越好。可以看到,PULSE 的分数最高。为了提供另一种感知质量度量,研究者还对感知超分辨率问题常用的自然图像质量评价(Naturalness Image Quality Evaluator, NIQE)分数进行了评估。具体来说,他们对每种方法在 1024×1024 分辨率上的 NIQE 分数进行了评估,其中输入分辨率为 16×16,缩放因子为 64。
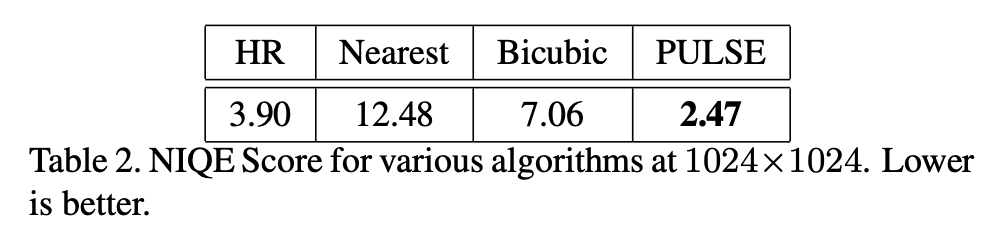
表 2:每种方法在 1024×1024 分辨率上的 NIQE 分数,分数越低效果越好。可以看到,PULSE 的 NIQE 分数最低。
最后,研究者对 PULSE 算法的鲁棒性进行了评估。该算法的主要目的是利用已知的降尺度算子来执行感知逼真的超分辨率任务。研究者发现,即使对于各种未知的降尺度算子,该方法都可以使用双三次降尺度(bicubic downscaling)实现充分的降级,具体如下图 6 所示:
图 6:研究者证实了利用不同降级算子时 PULSE 的鲁棒性。
版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请留言联系删除,感谢合作。