IV、AUC和KS是信贷建模中常用的三个指标，IV一般用于变量筛选，而AUC和KS用来衡量分类模型效果。

从三者的定义来看，IV是从条件密度函数的角度出发衡量变量对好坏样本的区分能力，而AUC和KS则是从条件分布函数的角度来来描述模型结果对好坏样本的区分能力，因此三者实际上是具有较高的一致性。

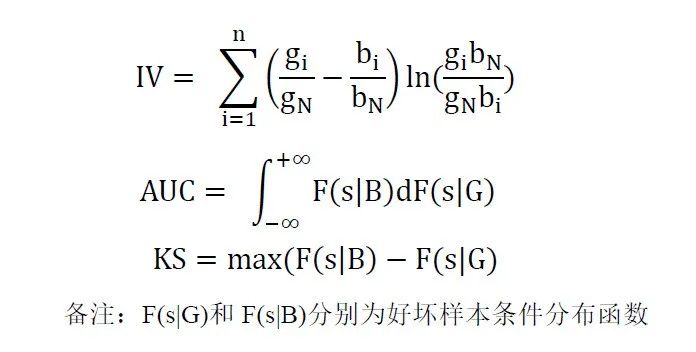
但由于他们的计算方式的不同，IV和AUC/KS会存在一定的偏离，我们很难从理论公式出发来推导出IV和AUC/KS之间确切的数学关系。影响这种偏离的原因主要有：

1. IV值会受分箱数量影响，因此即使是同样的样本，随着分箱数量改变，IV值也会发生改变，而AUC和KS是不变的；

2. AUC和KS利用了累积分布函数的信息，因此对变量的排序性敏感，而IV并没有用到这种累积的信息，因此如果我们对调任意两箱的好坏样本率，IV并不会改变，而AUC和KS却会随之改变。

本文通过抽样模拟的方式来探索IV和AUC/KS之间对应的数值关系，以便能够根据IV值快速推断出其对应的AUC/KS区间，解决在实际业务场景中数据不可得的问题。

本文具体抽样方法为：

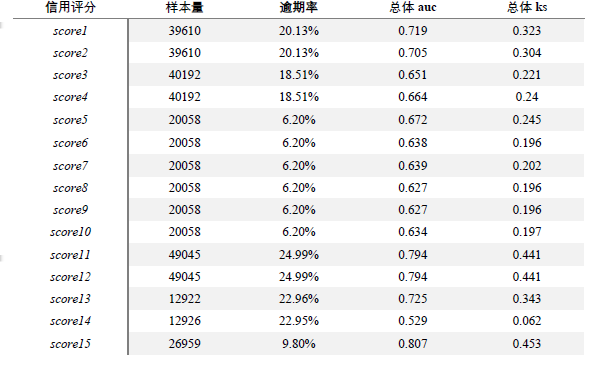
选取15款AUC不尽相同的信用评分产品，每次从单个评分中无放回地随机抽取1w数据，计算抽取的1w样本的iv、auc和ks，重复1000次（每次重复改变抽取的随机种子，以确保抽到不同样本）。

同时为了测试不同逾期率对IV和AUC/KS对应关系是否存在影响，我们将好坏样本比分别控制在1%、4%、7%、10%、13%、16%和20%七种情景下抽取样本，这样单个信用评分产品在每个逾期率情景下对应可获得1000条IV、AUC和KS数据(IV计算方式选用等频分箱，分箱数量为10箱)。

下表为选取的15款信用评分的基本信息：

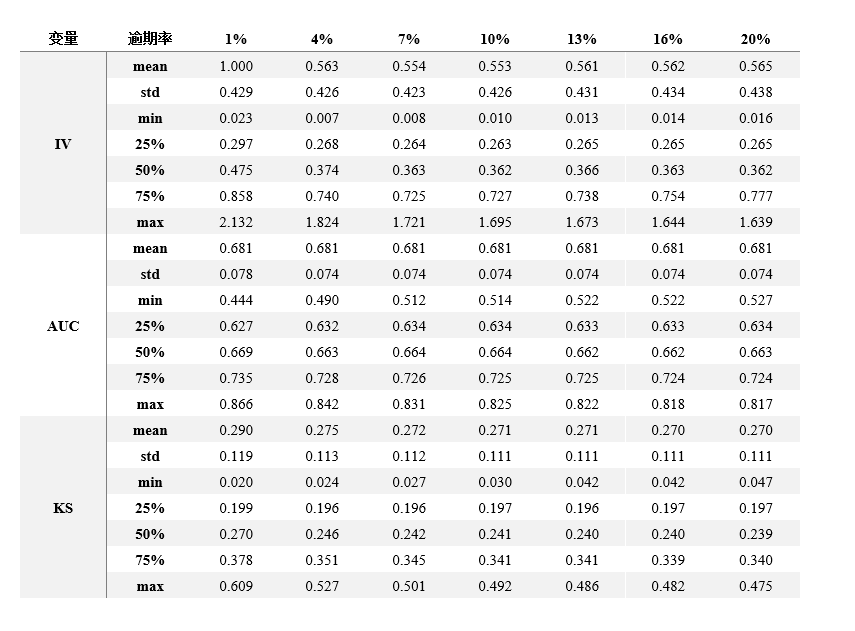
由于我们每次重复抽样采用不同随机种子，因此抽取样本和总体样本之间存在一定偏差，从单个评分中抽样样本的AUC/KS和其总体样本的AUC/KS也会有差距，具体表现为抽样样本AUC/KS值围绕总体样本的AUC/KS上下波动，而我们正好利用抽样误差可以从同一款信用评分中获取尽可能多的AUC/KS的不同取值。

尽管利用抽样误差可获取AUC/KS的不同取值数据，但同一款信用产品的抽样所得的AUC/KS值不会偏离其总体AUC/KS值太远，因此我们需要不同的信用评分产品(主要信用评分总体AUC要不同)中进行抽样，使AUC/KS能够尽可能覆盖到更大范围的值域。

抽样数据分布情况如下表所示：

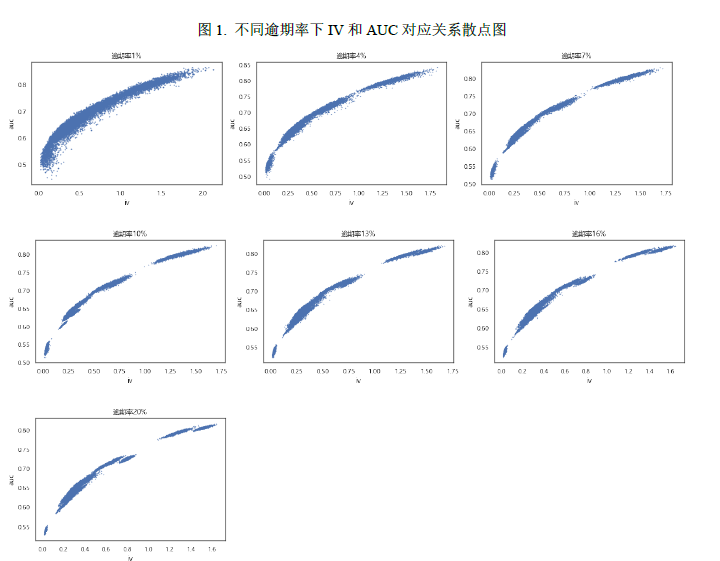
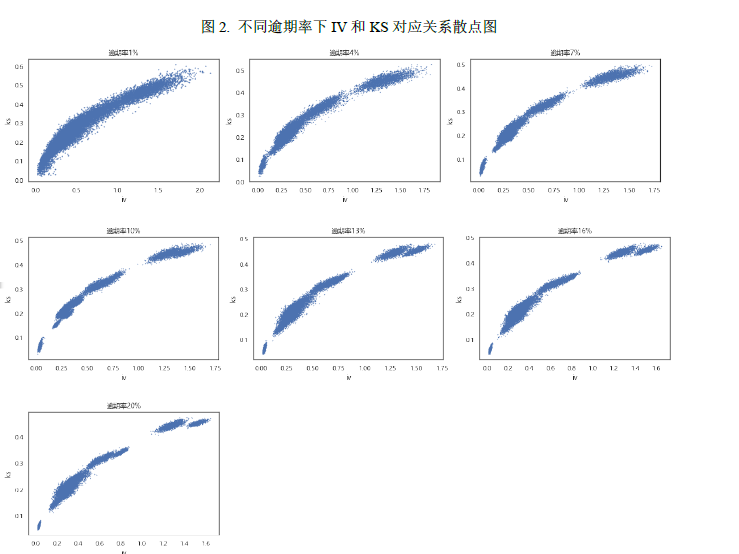
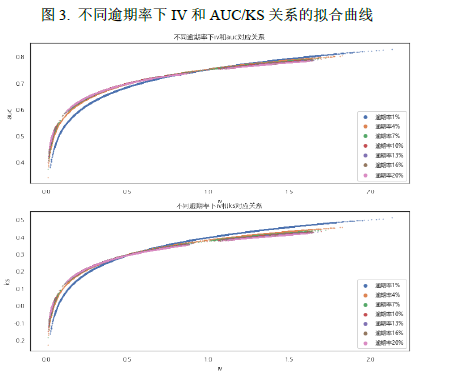
我们拟合了不同逾期率下IV和AUC/KS的关系曲线，发现不同逾期率下IV和AUC/KS拟合曲线参数都非常接近，因此我们将所有逾期率下的数据合并，来拟合IV和AUC/KS对应的经验公式。

从上面的散点图可以看出，IV和AUC/KS关系呈现凸函数的特征，也即随着IV增大，AUC/KS增大的程度减缓。这也很符合直觉，从理论上来看，IV的取值范围在[0, )，而AUC取值在[0, 1]，因此当IV高于某个值之后再增加，AUC对应的增加范围并不会很大。

这里我们选用同样具有凸函数的特征的对数函数来拟合两者之间的关系：

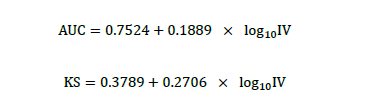
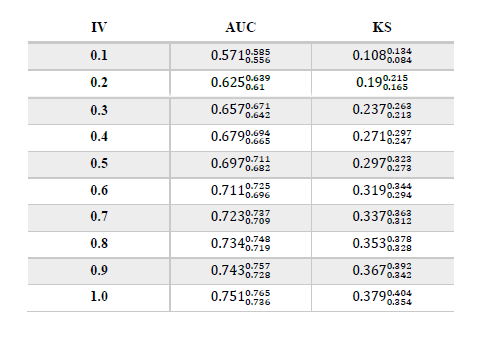
最后，通过计算拟合残差在50%的置信区间可以得到如下的对应关系表：