数学台球是我们平时在普通台球桌上打球的一个理想化的产物。在数学台球中，球会遵循和普通台球一样的规律弹跳，但是这时的球本身是没有质量的，因而也不会有摩擦存在。同时桌边和桌角也没有球袋来吞球，这意味着球会在球桌的侧边无限次地弹来弹去，永不停息。

数学台球的一个迷人之处，在于它提供给我们一种用于寻找两个自然数的最大公因数和最小公倍数的几何手段。如下面这个图所示这样（球从左下角出发，经多次反弹后到右下角停止），我们取自然数40和15，最后得到的最大公因数是5，最小公倍数则是120。那么这个结构的工作原理是什么呢？我们接下来就来看一看。

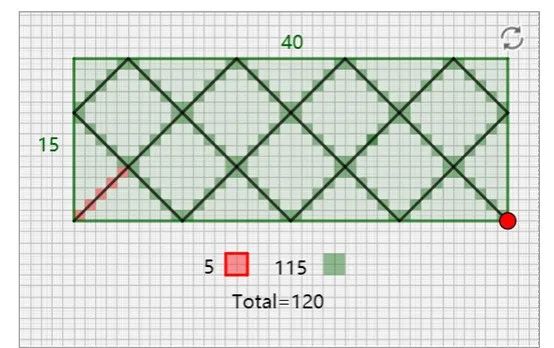
自然数40和15的最大公因数是5，最小公倍数是120

完整动画可以戳这里

这里是一些基础概念。设想给定两个正整数a和b，两者中的任何一个都不是另一个倍数（一个是另一个的倍数这种情况比较简单，我们留给读者自己证明）。对于台球桌，我们采用一个长宽为a和b的矩形。我们从桌子的一角同侧边成45°把球击出，台球从桌子侧边弹来弹去，在这过程中速度不会减弱减小，并且根据反射定律，台球每次到达一个侧边时都会以45°反射（这样一来路径只会向左或向右转90°）。台球的路径就由这些线段组成。

我们可以断定，在这样一组路径之后，球最终会击中另一个角。而球击中这个角落之前所经过的路径长度除以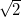，就是a和b的最小公倍数；如果我们把台球桌分解成一个一个单位方块（即边长为1的正方形），最小公倍数就等于台球走过的路径上单位方块的数目。

我们同时还能断定，整个路径一定会出现相交点。在起点不远处就会出现一个相交点。两个给定自然数的最大公因数就等于从起点到最近的相交点的距离除以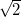。它还等于从起点到第一个自交点的路径穿过的单位方块数。

在镜中观察一个物体时，你会觉得这个物体就在镜子后面。值得注意的是，这时有三个点是对齐的：标记位置的点、在镜子上看到物体的反射点以及你“看到”的镜中的虚点。为了证明我们上面的几个推断，我们将利用这个简单的想法，把台球桌的侧边看成镜面。

我们把a和b的最小公倍数写作  ，它是同时是a和b的倍数的最小的自然数。再给出某些正整数m和n，我们可以把写出 。举个例子，对于和，然后我们可以写出来

在这里m=3，n=2。

这里给定的两个数字a和b，其中哪一个都不是另一个的倍数，我们先做一个边长为  的正方形。它可以分解成  个长宽为a和b的长方形。显然这是因为m个a相加，和n个b相加都等于 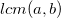 。因为  是a和b的最小公倍数，我们的正方形是用长宽为a和b的长方形能铺满的最小的正方形了。我们把这些长方形中左下角的记作R，右上角的记作S（如下图所示）。

在这个例子中a=4，b=6，最小公倍数就是3x4=2x6=12，所以这个正方形的边长是12，里面包含了3x2=6个长方形。

现在我们从左下角开始，到右上角结束，画出这个正方形的对角线d。

从d中我们要画一条曲折的路径t，通过重复反射之后，它整个都落在长方形R中。路径t就是数学台球在长方形R内移动的路径。

我们从右上角的S开始，沿同对角线d相交的侧边做一个镜像，在我们这个例子中，这条侧边也是长方形S下方的长方形的侧边，我们把那个长方形记作S’。

沿S的底边做一个镜面反射，把部分对角线反射到下面的长方形中去

现在把S’沿与d交叉的边再次反射（在我们的例子中，是沿S’的左边，注意不是往上反射回S）。

把S’反射到左边

一直这样操作下去，不停把长方形沿与d交叉的侧边进行反射，直到最终到达左下角的长方形R里。这样重复的反射之后，我们就由对角线d得到了曲折路径t。

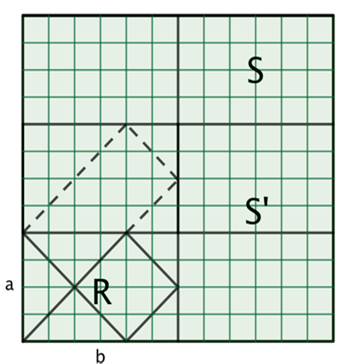
最后的反射就得到了在长方形R内部的路径t。

路径t就是从R的左下角射出的球在R的侧边成45°反射之后得到的路径。从下图可以更清楚地看到。（动画可以戳这里）

为了证明确实如此，我们先回想一下，球每次和侧边撞击之后，都会向左或者向右转90°弯。可以看到路径t确实是这样。从下面的图里也很好解释这一点。

路径t每次碰上R的侧边都会转90°弯。

因为路径t是S的不断沿长方形的侧边反射得到的，t的终点也是S的右上角顶点不断反射得到的，所以t的终点也是R的一个顶点。

路径t的长度则是等于对角线d。因为任意正方形的对角线长度都等于边长的倍（这一点来自于毕达哥拉斯定理），所以有：

是路径t的长度。重新组合一下，我们有：

这就是我们想要证明的结论：球的路径长度除以，就是a和b的最小公倍数。

对于我们所举的例子而言，这个方法很完美，但是我们能保证它对任意值的a和b（它们彼此不是对方的倍数）都成立吗？唯一可能出错的地方在于，对角线d在正方形内部就经过了一个长方形的某一个顶点，这样的话，我们就无法确定哪一边能反射到角上了。

我们接下来证明这一点是不可能发生的。我们很容易知道，对角线上的任何一点P都能确定一个正方形：只要垂直向下、水平向左画直线与原正方形相交就可以了。

对角线上的任何一点都能确定一个正方形。

如果这样一个点也正好是某一个长方形的顶点，那么我们这个小正方形就应该能够被长宽为a和b的长方形铺满——但这是不可能的，正如我们之前所说，边长为  的正方形已经是能够被铺满的最小正方形了。

我们已经说明了 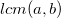 等于路径t的长度除以，接下来我们来看看单位方块。

要数一下路径t穿过的单位方块（即边长为1的正方形）的个数，我们要先把长方形R画成坐标系统的形式。横轴和纵轴如下图所示，单位方块的顶点的坐标都是整数。

长方形R和它构成的坐标系统。其中路径t经过的单位方块的顶点的坐标用红色标出。

很明显如果t穿过了一个单位方块，它同时会沿着其对角线运动。我们还可以看到，如果一个单位方块的顶点落在了路径t上，它的横纵坐标加起来等于一个偶数。任何一个单位方块都只有两个这样的顶点，它们位于一条对角线的两端，所以，t只能经过单位方块的两条对角线中的一条。

路径t同时也不可能两次经过单位方块的对角线，无论是两次方向相同还是两次方向相反。这一点我们留给读者自己证明。读者需要证明t的终点不同于它的起点。这样的话，m和n中至少有一个是偶数，同时要注意t的终点是由S的右上角的顶点不断反射而成的。

我们现在知道，路径t不会穿过某个单位方块超过一次，同时它总是沿着单位方块的对角线方向。因为单位方块的对角线长度是，t经过的单位方块的个数就是：

这和我们之前的推断一致。

我们之前断言说，a和b的最大公因数  是从起点到最近的自交点的距离除以，也等于从起点到第一个自交点的路径穿过的单位方块数。

我们先假设  ，这样的话a和b的最小公倍数等于二者的乘积 （这一点读者可以自己证明）。根据我们之前的结果，那路径穿过的单位方块的个数也是  。因为长方形的长宽是a和b，那它内部就一共有 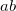 个单位方块。而因为路径不会穿过任何一个单位方块超过一次，那么路径就必须穿过了所有单位方块。

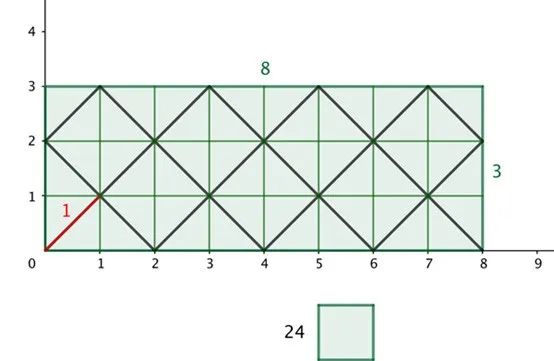
在这个例子中a=3，b=8，最大公因数是1，最小公倍数是24。

我们已经知道，落在路径t上的单位方块的顶点的横纵坐标相加都等于偶数。反过来，路径t经过了每一个单位方块，意味着每一个坐标和为偶数的顶点都落在了t上。

这意味着(0,0) 、(0,2)  、(2,0)  和(2,2)这些点都在t上。而这只有当(1,1)是t的一个自交点时才成立。

因而(1,1)是t和自身相交得到的一个交点，它也是沿着t离(0,0)最近的点。(1,1)到(0,0)的距离是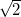，除以就得到了1，即上面例子中a和b的最大公因数。从(0,0)到(1,1)沿t穿过的单位方块的数目也是1。这就证明了在这个例子中我们的推断。

如果  ，我们可以通过一个因子  来重新调整整个坐标的标度：把a和b除以它们的最大公因数  ，我们会得到两个最大公因数为1的正整数。这时再重复上面的构造，然后再把横纵坐标轴乘以  ，把整个坐标系统放大。单位方块就变成边长为  的正方形。所有和具体长度值无关的几何性质（比如路径形状，经过的顶点等等）都不会受坐标缩放的影响。

在这个例子中a=9，b=24，最大公因数是3。除以3之后我们得到3和8，和我们举的例子一样。把前面的例子中的情况扩大3倍，就得到了新的图像，单位方块就变成了边长9的正方形。

路径第一段中离起点最近的自交点，距离起点的长度是  ，从而 是等于从起点到第一个自交点的路径穿过的单位方块数。