你的班里有没有两个生日相同的同学?
以下文章来源于大小吴的数学课堂 ,作者大小吴
致力于做有趣的数学科普
你是否以前在上学的时候想过这样一个问题:我们年级里(或者班级里)是否有两个生日一样的同学?如果一个年级有400人,那么就必然至少会有两个同学生日相同(因为一年只有365天或366天)。实际上,我们通过数学计算可以得知其实并不需要那么多同学,仅仅只需50人的班级中,就有非常高的概率会出现这种情况,很反直觉吧!今天小编来和大家探讨一下概率论中非常著名的生日问题。

1 极端的情况
对于生日问题我们可以这样描述:
假设每个同学的出生日期都是相互独立的,并且每个同学都等可能地出生在一年中的任何一天(2月29日除外),那么要有多少人才能保证其中至少两个同学的生日在同一天的概率
我们不考虑闰年,假设一年只有365天,因此只要一个年级有366个同学就一定会出现“至少两个人的生日在同一天”,因此答案必然是2到365的某个数。
想想另一种极端情况,如果一个年级有184个同学,那么至少两个人的生日在同一天的概率一定不小于50%,为什么呢?想想如果前183个同学的生日互不相同(比方说这183个同学的生日正好就是一年的第1~183天),那么对于第184个同学来说,他与前面183个同学中的某人同一天生日的概率就至少为50%!这并不难理解:因为一年中过半的日期已经被占用了,最后一个同学要么和前183个同学中的某人同一天生日,要么生日是在剩下的182天中。
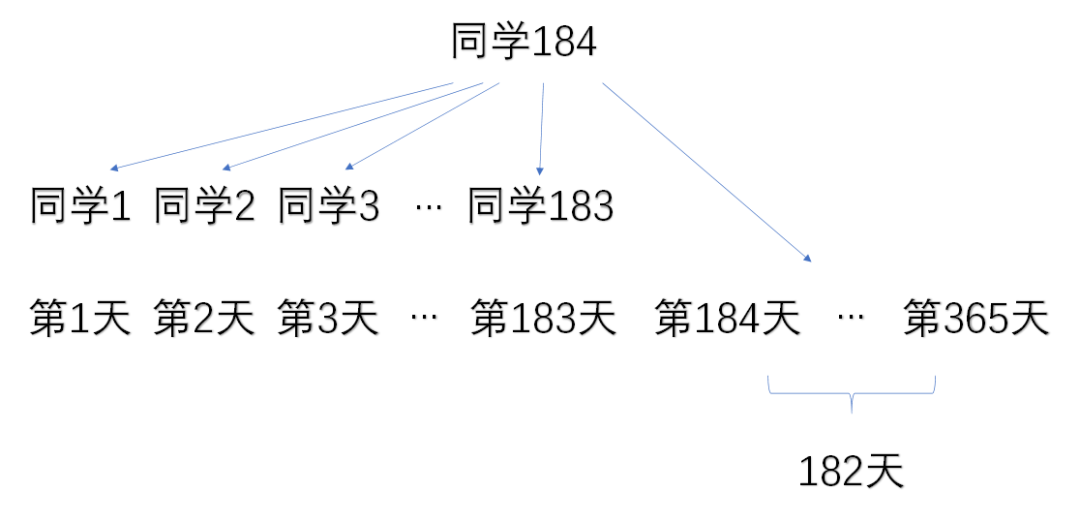
这样我们就又缩小了范围:这个问题的解一定满足
并且,直觉告诉我们,肯定是人越多(越大),“至少两人生日在同一天”的概率越大。
2 穷举法
我们可以尝试用穷举法来求解这个问题,比如说一种简单的情况:当时,这两个人所有可能的生日排布方法一共有
这很容易理解:因为对第一个人来说,他的生日有365种可能,第二个人也有365种可能。在这133225种组合中,两个人生日在同一天的组合只有365种,这也不难理解:如果两个人生日在同一天,那么只要选定了第一个人的生日,第二个人的生日就只有唯一一种可能。
因此当只有两个人的时候,概率的计算非常简单:
再来看的情况,那么易得所有可能的生日排布方法有
计算分母很容易,但在计算分子时要特别当心。因为我们要算的是“至少两人生日在同一天”,因此这里我们需要分类讨论:有且只有两个人生日在同一天 三个人生日在同一天
对于第一种情况,我们可以这样计算:假设前两个人生日在同一天,第三个人生日与他们不同,则共有
(第一个人的生日可以是一年365天中的任何一天,第二个人的生日必须与第一个人相同,而第三个人的生日只能从剩下的364天中选取)类似地,易知这种情况会出现3次:
| 第一个人 | 第二个人 | 第三个人 |
|---|---|---|
| 相同 | 相同 | 不同 |
| 相同 | 不同 | 相同 |
| 不同 | 相同 | 相同 |
因此这种情况包含的组合数为
别忘记还有一个很特殊的情况:三个人生日相同,这种情况包含的组合数为365种。
这样我们可以计算三个人时的概率:
从两人的到三人的,概率确实增大了,符合我们的直觉。但是遗憾的是,这个概率离还十分遥远,而且我们会发现当变得越来越大时,整个计算过程就是一场噩梦,因为情况会越来越复杂,整个过程需要更全面地分类讨论,这不是我们所希望看到的。
3 计算对立事件的概率
因此,穷举法在这个问题中不是一个理想、高效的方法,我们需要更好的思路。
在概率论中,计算对立事件的概率——不发生的概率——有时往往比直接计算事件的概率容易很多。如果我们知道事件不发生的概率是,则发生的概率就是,对于对立事件来说,两者必有其一发生。
想想这对解决生日问题有什么帮助呢?很显然,如果我们记事件
则其对立事件为而计算“所有人的生日都互不相同”这件事的概率是容易的,举个例子,当时,其概率为
当时,其概率为
沿着这个思路,对于一般情况来说,当人数为时,其概率为
使用连乘符号,我们可以把这个结果改写成
也许你对这个符号不太熟悉,它是由求和符号推广而来的,我们知道相应地,有
对上面的表达式再进行一些简单的处理,得到
4 程序实现
上述这个代数式计算的是“至少两人生日在同一天”的对立事件“所有人的生日都互不相同”的概率,因此我们需要使得
大数的阶乘计算起来并不容易,我们可以借助数学软件帮助我们计算,设计一个简单的解决生日问题的程序:
noshare = {{1, 1}};
share = {{1, 0}};
currentnoshare = 1;
For[n = 2, n <= 50, n++,
{
newfactor = (365 - (n - 1))/365;
currentnoshare = currentnoshare*newfactor;
noshare = AppendTo[noshrae, {n, 1.0 currentnoshare}];
share = AppendTo[share, {n, 1.0 - currentnoshare}];
}]
Print[ListPlot[share, AxesLabel -> {"人数n", "概率P"}]]
我们可以得到如下图像:
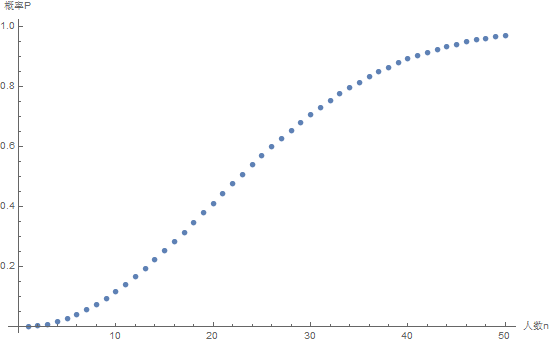
从图中我们可以看出,当时,概率约为,当时,概率已经攀升到了,当时,概率变为了惊人的!也就是说,在一个50人的班级中,将有非常大的可能会有两个同学生日在同一天!下次你便可以和你的小伙伴打赌了:嘿,朋友,你信不信咱们班一定有两位同学是同一天生日?
参考文献[1](美)史蒂文·J.米勒.普林斯顿概率论读本[M].李馨译.人民邮电出版社,2020.
来源:大小吴的数学课堂
编辑:tzy
近期热门文章Top10
7. 300年后,他击败了牛顿
8. 量子世界里有两只猫,一只是薛定谔的猫,另一只是......
