数学家排名，高斯第二牛顿第三？！看完第一的简历，他果然比牛顿还牛逼......

爆炸吧知识今天

如果让你给数学家排名，你会怎么排？

谁排第一？

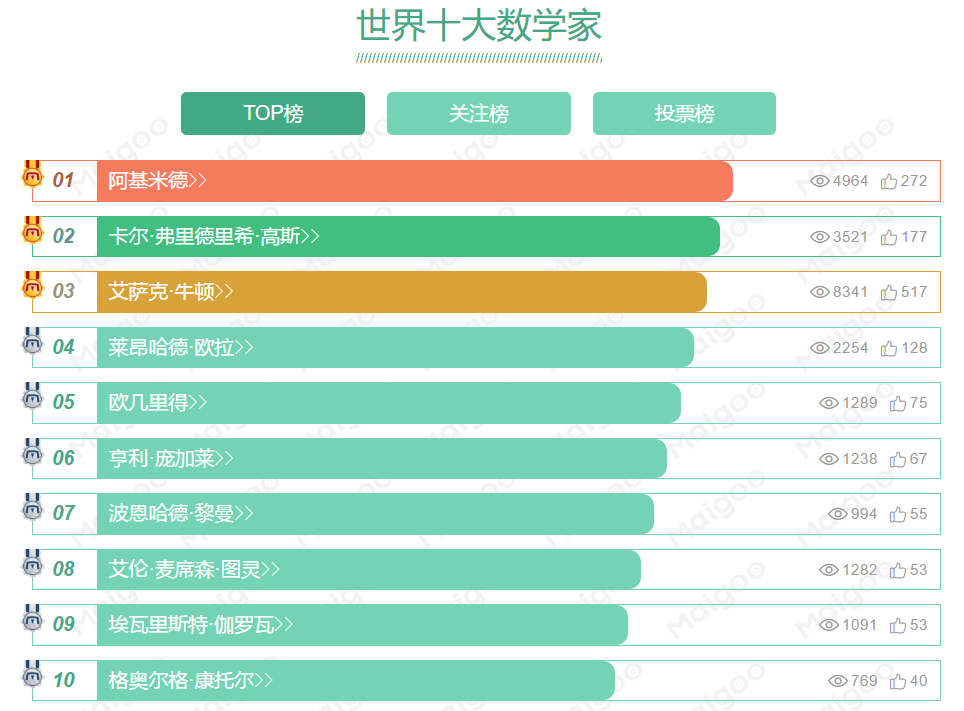
高斯？阿基米德？

还是其他哪位数学神仙？

今天早上超模君发现，在国内某排行网站上，由网友投票选出来“世界十大数学家”里，

名列前四的分别是阿基米德、高斯，牛顿和欧拉：

在人类过往2600年的数学历史长河里，数学名人堂里大师济济，

这四位数学家是凭什么，被网友推选上数学总统山的呢？

超模君今天就来和模友们侃一侃，关于“四大数学家”的生涯简史。

阿基米德

公元前287年~公元前212年

“给我一个支点，我能翘起整个地球。”

作为有史以来第一个因为“抬杠”出圈的数学家，阿基米德对人类数理文化的推进作用堪称空前绝后。

单论他在数学方面的成就，连起来就可以绕地球三圈：

1. 给出许多求几何图形重心，包括由一抛物线和其网平行弦线所围成图形的重心的方法；

2. 采用不断分割法求椭球体、旋转抛物体等的体积，这种方法已具有积分计算的雏形；

3. 算出球的表面积是其内接最大圆面积的四倍，又导出圆柱内切球体的体积是圆柱体积的三分之二；

4. 利用“逼近法”算出球面积、球体积、抛物线、椭圆面积，利用割圆法求得π的值介于3.14163和3.14286之间，其思想实质预告了微积分的诞生；

5. 研究出螺旋形曲线的性质，现今的“阿基米德螺线”曲线，就是因为纪念他而命名；

6. 在《数沙者》一书中，创造了一套记大数的方法，简化了记数的方式......

高斯

1777年~1855年

高斯，不是忙着打怪的奥特曼，而是被誉为“数学王子”的那位。

从“3岁就能纠正父亲账本里的错误”开始，高斯的数学生涯可谓一路绿灯，但凡是个懂数学的人，都不能站着看完他的简历：

16岁时，导出二项式定理的一般形式，将其成功的运用在无穷级数，并发展了数学分析的理论；

18岁时，发现了质数分布定理和最小二乘法；

19岁时，仅用尺规便构造出了17边形，并为流传了2000年的欧氏几何提供了自古希腊时代以来的第一次重要补充；

24岁时，在以最小二乘法为基础创立的测量平差理论的帮助下，测算天体的运行轨迹；

1818年至1826年间，写出了近20篇对现代大地测量学具有重大意义的论文，推导了由椭圆面向圆球面投影时的公式，并作出了详细证明......

牛顿

1643年~1727年

时常以卷发造型出现在教科书插画中、数理两开花的牛爵爷，虽然他在数学方面的硬荣誉不如物理上那般惊天动地，但依旧对整个人类数学史产生了举足轻重的影响：

1. 微积分发明人，是最早将微积分发展成有效工具的人之一；

2. 用微积分语言成功阐述物理规律，大大提高了数学在自然科学中的价值。

不但证明伽利略的利用数学描述物理规律的思想是非常成功的，同时也让后世的科学家意识到了数学的重要性，让数学成为描述规律的工具的重要性；

3. 将数学和物理成功结合又促进了数学家对物理学以及自然规律重要性的认识......

欧拉

1707年～1783年

9岁时看完牛顿的《自然哲学的数学原理》，这是欧拉；

在双眼失明的情况下，创立分析力学和刚体力学，这也是欧拉。

总之欧拉就是牛逼，从小牛逼到大：

1729年，给出了伽马函数的定义；

1732年，得到了所谓的欧拉-麦克劳林求和法；

1734年，给出了欧拉常数；

1735年，攻克了巴塞尔问题（1740年发表），给出了答案；

1741年，解决了七桥问题，这是图论领域最早的文献；

1744年，给出了著名的欧拉恒等式；

1748年，出版了《无穷分析引论》；

1755年，出版了《微分学》；

1768-1770年，出版了三卷本《积分学》，还出版了影响甚广的《代数导引》......