编译：琰琰

第一性原理是一个物理学概念，可以简单理解为一个定理，或者定理的推论。

同为评价事物的依据，第一性原理和经验参数代表两个极端。经验参数是通过大量实例得出的规律性的数据，而第一性原理是某些硬性规定或推演得出的结论。

在深度学习理论中，经验性学习是学者们常常使用的研究方法，它为深度学习的发展提供了有价值的指导。然而，这种基于“经验参数”的方法并没有解决神经网络可解释性差的问题。

而在近期，已经有一些深度学习的理论性工作开始受到关注。比如今年4月，UC Berkeley马毅教授发表报告Deep Networks from First Principle，从第一性原理的角度，阐述了最大编码率衰减（Maximal Coding Rate Reduction,   MCR^2）作为深度模型优化的系列工作。

近日，来自巴黎INRIA研究中心的Francis Bach教授也分享了他对第一性原理在深度学习领域应用的思考。这篇新书稿名为“learning Theory from Fist Principles”，在这本书中，Francis Bach展示了学习框架的最新研究成果，以及第一性原理在学习理论中的证明结果。

书稿链接：https://www.di.ens.fr/~fbach/ltfp_book.pdf

根据作者介绍，这本书稿摘自Francis Bach在2020年秋季学期一堂课的讲稿。这堂课采取的是线上授课，他希望撰写书稿对课堂内容进行一个更详尽的整理。

本书的目标是展示学习理论中被广泛使用的学习架构的最新研究成果，主要面向以理论为导向的学生，以及希望对机器学习算法和相关领域中的基础数学有更好理解的学生，他们是对计算机视觉或自然语言处理等学习方法感兴趣的主要群体。

在书中，作者以简化的语言阐述了第一性原理的诸多证明结果，并通过简单且相关的示例展示了学习理论的重要概念。即使在没有证明的情况下，书中也呈现了一般结果。考虑到第一性原理的概念是主观的，读者在学习之前需要对线性代数、概率论和微积分等基础知识有一定的了解。

学习理论部分是本书的核心章节。考虑到算法的实践性，书中描述的所有算法框架都是经常使用的。此外，大多数学习方法都提供了简单的说明性实验，并附上了部分代码（Matlab、Julia和Python），以便学生在综合实验中看到算法是简单且有效的。

本书在章节设定上是任意的，也是基于个人兴趣的，因此，如强化学习、无监督学习等许多重要的算法框架可能并未出现。以下是作者目前正在扩充的一些附加章节：

– 集成学习（Ensemble learning）

– Bandit优化（Bandit optimization ）

–概率方法（ Probabilistic methods ）

– 结构化预测（Structured prediction）

基础

第一章：数学基础

• 线性代数：避免冗长和错误计算的技巧。

• 集中不等式：对于n个独立的随机变量，经验平均值与期望值之间的偏差为O（1/√ n），那么O是什么含义？

• 决策理论（损失、风险、最优预测）：给定足够大的数据和计算资源，最优预测和性能是什么？

• 统计学习理论：算法何时“一致”？

• 没有免费的午餐定理（NFL）：没有假设，学习是不可能的。 

第三章：线性最小二乘回归

• 普通最小二乘估计：最小二乘回归与线性参数化预测导致线性系统的大小为d（预测的数量）。

• 在固定设置下的保证：当假定输入为确定性的，且d>n时，过度风险等于

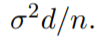
• 岭回归：随着ℓ2 正则化，过度风险边界变得与维数无关，并允许高维特征向量，其中d>n。

• 随机设计环境中的保证：虽然很难表现出来，但它们有相似的形式。

• 性能下限：在规范下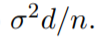，比率不可再提高。 

Part 2

学习算法的一般化界限

第四章：经验风险最小化

• 风险的凸化：对于二元分类，可以通过凸代理实现最优预测。

• 风险分解：风险可以分解为近似误差和估计误差之和。

• Rademacher complexities：用于研究估计误差和计算期望之间均匀偏差的强大工具。

• 与统计量渐近分布的关系：经典的渐近结果提供了经验风险最小化行为的精细描述，它们提供了性能的渐近极限作为一个定义良好的常数乘以1/n，但它们不具有小样本效应的特征。

本章主要介绍基于经验风险最小化的方法。在研究必要的概率工具之前，首先探讨了输出空间不是向量空间的问题，例如Y={−1，1}，可以用所谓的损失函数的凸代理重新表示。 

第五章：优化机器学习

• 梯度下降：对于条件良好的凸问题，一阶优化算法收敛速度呈指数级增长。
• 随机梯度下降（SGD）：大规模机器学习的一阶算法，收敛为1/t或1/√ t、 其中t是迭代次数。
• 通过SGD的泛化边界：只需对数据进行一次传递，就会避免出现过拟合的风险，并获得未见过数据的泛化边界。
• 方差缩减：当最小化强凸有限和时，这类算法以指数级速度收敛，但迭代复杂度很小。

本章主要提出一种基于梯度下降的优化算法，并分析了其在凸函数上的性能。作者表示将考虑应用于机器学习之外的通用算法，以及专用于机器学习的算法（例如随机梯度方法）。

第六章：局部平均法

• “线性”估计器：为每个观测值分配权重函数，以便每个观测值可以用相应的权重为标签投票。

• 分区估计：将输入空间分割成不重叠的单元，预测值是分段常数。

• Nadaraya-Watson估计：又称kernel regression，核回归，它为每个观测值分配一个与其在输入空间中的距离成比例的权重。

• k近邻：每个观测值为其k个近邻分配相等的权重。

• 一致性：所有这些方法都可以证明学习复杂非线性函数的收敛速度为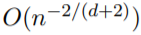，其中d是基本维度，并导致维度诅咒。

第七章：核方法（Kernel methods）

• 核与再生核定理：利用核函数和观测值可以及时地对无限维线性模型进行学习。

• R的d次幂上的核：这类模型包括多项式和经典Sobolev空间（具有平方可积偏导数的函数）。

• 算法：凸优化算法可以应用于理论保证和许多专门的发展，以避免计算核矩阵的二次复杂性。

• 规范模型的分析：当目标函数在相关函数空间中时，可以用与维数无关的速率进行学习。

• 错误规范模型的分析：如果目标不在RKHS中，且目标函数存在少量导数的最坏情况下，维数灾难无法避免，但该方法可以适应任何数量的中间平滑。

• 岭回归的sharp分析：对于平方损失，一个不必要的分析引起Rd中各种情况下的最佳速率。

第八章：稀疏方法（Sparse methods）

• ℓ0 penalty：对于线性回归，如果最优预测器有k个非零值，那么可以在平方损失中用ℓ0 penalty替换速率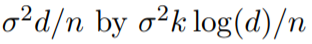（这在计算上很难）。

• ℓ1 penalty：在较少的假设下，可以得到一个与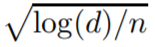成比例的慢速率ℓ1 penalty和有效算法，而快速率需要非常强大的设计矩阵的假设。

  
  

第九章：神经网络（Neural networks）

• 单隐层神经网络：使用简单仿射函数与附加非线性的组合。

• 估计误差：参数量不是估计误差的驱动因素，各权重的范数都发挥着重要作用。

• 逼近性质和普适性：由于“ReLU”激活函数对线性结构的适应性，逼近性质可以被表征，并且优于核方法。

Part 3

专题

第10章：Implicit bias of gradient descent

• 梯度下降的隐式正则化：对于线性模型，当存在多个极小值时，梯度下降技术往往收敛到最小欧氏范数的一个。 

• 双下降：对于用梯度下降技术学习的非正则化模型，当范围扩大，且参数量超过观测值数时，测试误差扩大，性能出现第二次下降。

• 两层神经网络梯度下降的全局收敛性：在没有宽度的限制下，梯度下降对一个非凸问题具有全局收敛性。

在本章主要介绍学习理论中的三个最新主题，它们都在一定程度上与“过度参数化”区域中的高维模型（如神经网络）有关，其中参数值大于观测值。

第11章：Lower bounds on performance 

统计下界：对于最小二乘回归，目标函数在某些特征向量中是线性的，或者在R的d次幂上的Sobolev空间中是线性的，监督学习的最佳性能恰好是通过本书前面介绍的几种算法实现的。下界可以通过信息论或贝叶斯分析得到。

优化下界：针对第5章中的经典问题可以设计硬函数，证明基于梯度下降的线性组合的梯度算法是最优的。

• 随机梯度下降的下界：与 对于凸函数和为了µ-强凸问题是最优的。

• 对于凸函数，速率与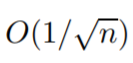成正比，用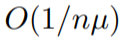求解µ-strongly凸问题是最优的。

AI科技评论

聚焦AI前沿研究，关注AI青年成长

1872篇原创内容

公众号

由于微信公众号试行乱序推送，您可能不再能准时收到AI科技评论的推送。为了第一时间收到AI科技评论的报道， 请将“AI科技评论”设为星标账号，以及常点文末右下角的“在看”。