你还记得在中学学习函数时背过的一个口诀吗？

“左加右减，上加下减”。

这个口诀描述的是函数图像平移时解析式的变化情况。

这句话的意思是：

左加右减指的是如果函数图像往左（右）平移个单位，则自变量加（减）.

上加下减指的是如果函数图像往上（下）平移个单位，则常数项加（减）.

如果你忘记了，我们来复习一下：以最简单的二次函数为例，如果将它向左平移4个单位，再向上平移2个单位，根据口诀“左加，上加”可以得到新的函数解析式

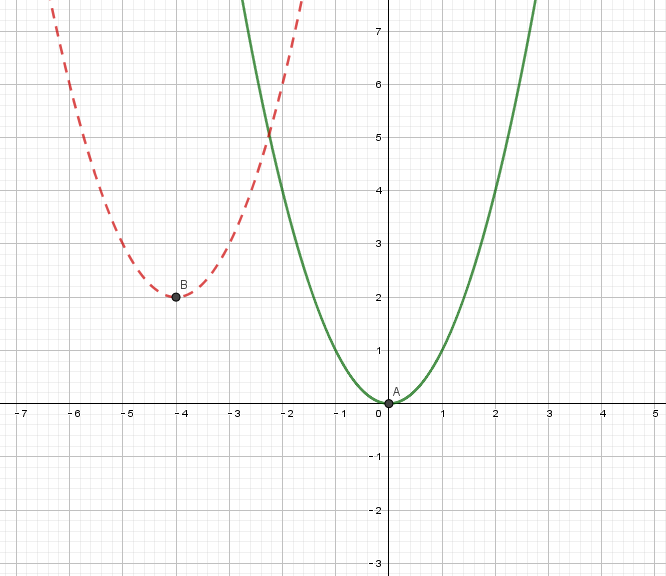
实际上，根据二次函数顶点的平移我们能够比较容易理解这件事。原函数的顶点为点，而由于函数平移后顶点也随之平移，变为了点，则根据二次函数的顶点式便能够写出新的函数解析式

二次函数可以根据顶点的平移来理解，那么对于一般的函数而言这个规则是否也成立呢？

在回答这个问题之前，请你回想一下中学时学习函数的心路历程，想必以前你有过这样的疑问：对于平面直角坐标系而言，朝上是轴正方向，那么既然存在“上加下减”的说法，直觉告诉我们对于朝右的轴正方向，相对应地应该是“右加左减”才对。这到底是怎么一回事呢？

其实，这是学习中学数学时一个常见的误区，我们不能简单地认为“上加下减”是因为轴正方向朝上。

我们应从如下角度去理解：首先，对上述新函数变换如下

这里可以看作是自变量，因变量，而对于函数图像来说，分别对应向轴负方向平移4个单位和向轴正方向平移2个单位。所以，这里其实并不矛盾，我们可以归纳出一般结论：

• 向轴负（正）方向平移，对于自变量来说是加（减），即左加右减。
• 向轴负（正）方向平移，对于因变量来说是加（减），即下加上减。

举个不恰当的例子，比如对于抛物线

说它不恰当，是因为它不满足函数的定义。不过我们依然可以根据这个规则去讨论它的平移。若将它向左平移4个单位，再向上平移2个单位，则根据上述规则可得到新的抛物线方程：

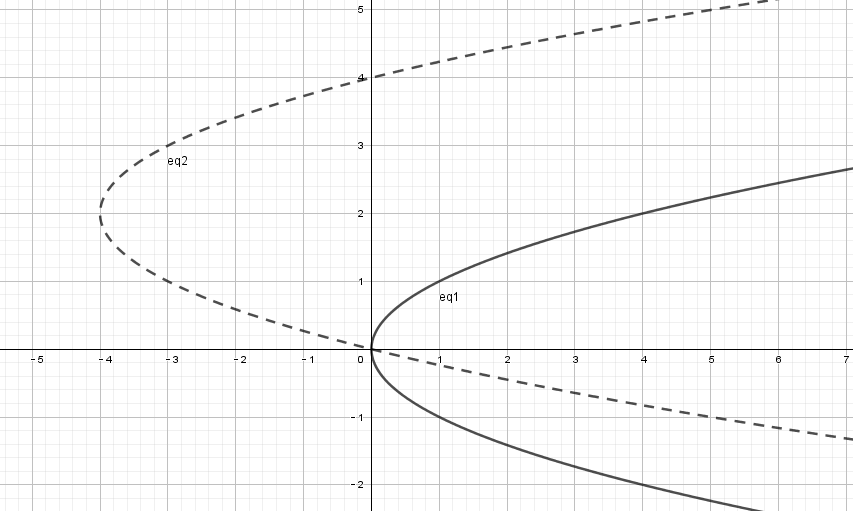
讨论到这里，你是否还是有疑问：为什么偏偏对于正方向而言是减，对于负方向而言是加呢？这和我们的认知依然是矛盾的。

我们以一个一般的函数为例，对于函数来说，将它向右平移个单位得到函数.

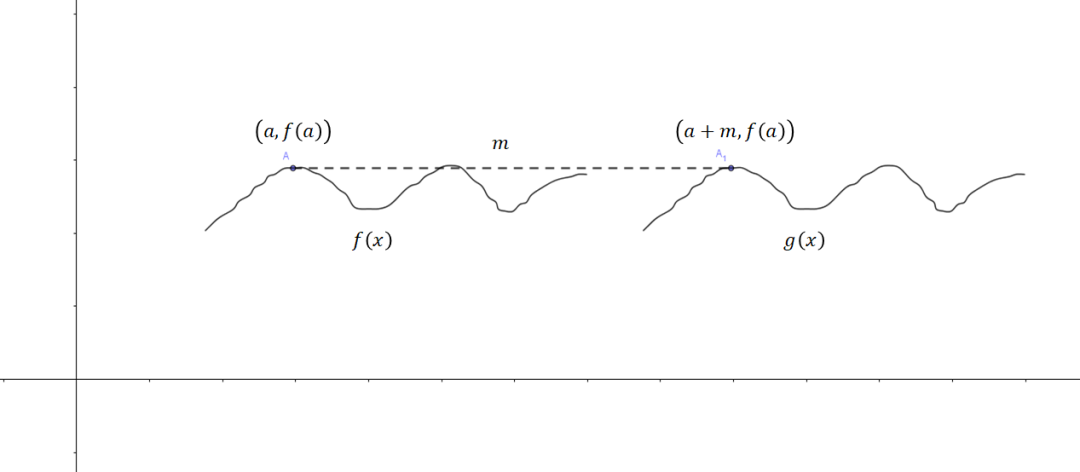
则原函数上的任意一点

经平移得到了点

因此

即

即

也就是说在新的函数解析式中，自变量会减去，这也即为“右减”。

通俗地说，对于坐标轴上的点，往右移动会使得的数值增加，而为了抵消这个增加量，函数里的自变量本身也要扣除相应的增加量，对于上下方向的轴也是同理。

你现在明白“左加右减，上加下减”的真正含义了吗？