阿基米德原理与浮力赝势能 ——在重力势能章节引入浮力之本质解释
以下文章来源于中国物理学会期刊网 ,作者高义华 等
中国物理学会期刊网(www.cpsjournals.cn)是我国最权威的物理学综合信息网站,有物理期刊集群、精品报告视频、热点专题网页、海内外新闻、学术讲座,会议展览培训、人物访谈等栏目,是为物理学习和工作者提供一站式信息服务的公众平台。

来源:中国物理学会期刊网
作者:高义华等
|作者:高义华1,† 鲁周超2 李文川3
(1 华中科技大学 物理学院&武汉光电国家研究中心)
(2 华中科技大学附属中学(光谷第一中学))
(3 湖北大学物理学与电子技术学院)
本文选自《物理》2021年第6期
引 子
阿基米德(公元前287—212年)是一位伟大的科学家(图1),是静态力学与流体力学的奠基人[1—3]。实际上,他的名字Archimedes很独特[2],非常适合阿基米德本人。“阿基”(Arche)是原理、规划、第一,“米德”(medes)即头脑、智慧、机智。完整地念他的名字,“Archimedes”就是“第一号头脑”。这位被后世称为最伟大的四位数学家之一的阿基米德,在科学上有众多建树,其中最著名的是人人皆知的冠以其名的计算浮力大小的“阿基米德原理”。

图1 阿基米德是人类历史上最伟大的四位数学家之一(其余三位分别是:牛顿、欧拉、高斯)。传说他在洗澡过程中发现浮力原理即阿基米德原理,于是解决了王冠的纯度问题(图片来源于网络[1,4])
话说有人赠送国王一顶金王冠[1,2],甚为精妙绝伦,堂皇庄严。但国王不知是否纯金,特委托阿基米德解此难题。阿基米德苦思冥想,久不得其解。某日,他在浴盆洗澡,突然大喊“尤里卡”,想到了解决办法:既然王冠是非规则物体,体积无法测定,但当浸入水中时排出水的体积即为王冠体积。将王冠重量再与具有同样王冠体积的纯金块相比,就可轻松知道王冠是否纯金。阿基米德的《论浮体》清楚地描述了浮力原理[2,3],其主要内容是:浸入液体中物体所受的浮力大小等于物体排开液体的重力大小。因为阿基米德是传奇人物,后世之人就把阿基米德浮力原理与洗澡辨识王冠纯度联系起来,增加了趣味性和可读性,以激发中小学生勤于思考,热爱科学的原始动力。
阿基米德用天才的大脑给出了浮力的大小与方向。但是,他没有对两个密切相关的问题给出明确的答案:(1)液面媒介的面积大小是否对结论有影响?(2)物体在液体中受浮力时,即使达到重力与浮力的平衡,是否需要考虑稳定状态?基于作者等在1989年的一个原始粗浅想法,这两个问题最近得到了清楚的答案[5],现将主要内容介绍如下。
阿基米德原理的本质与适用液态媒介表面积
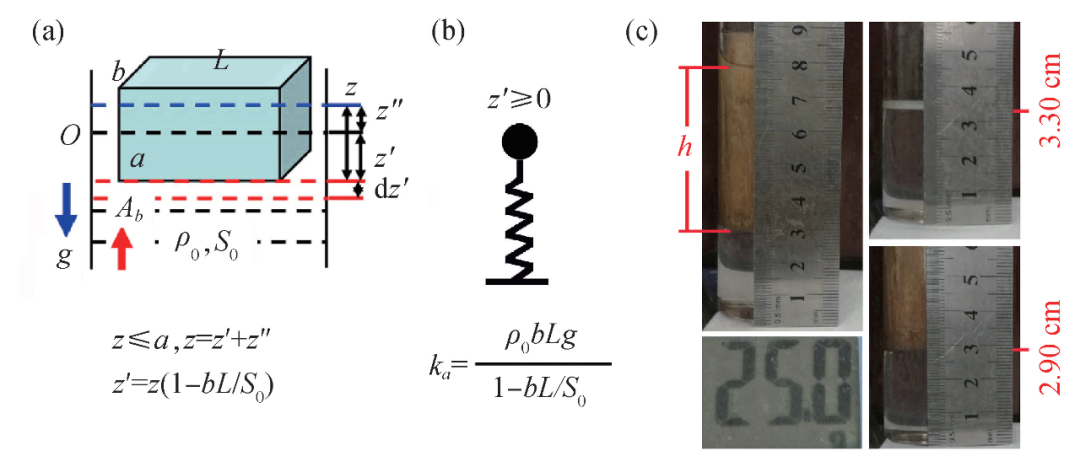
物体在液面上的稳定状态和浮力赝势能
现在回答第2个问题。在一般情况中,大家默认液面面积无穷大,容易忽略木块浸入液体后重力势能的增加。因为浮力大小只由浸入体积决定,且垂直向上,所以可将浮力视为一个保守力,且引入一个浮力场Ab [5],
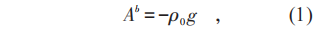
在无限大液面情况下,木块以 b×L 底面浸入时,力平衡时木块下降的绝对高度和浸入深度都是aρ/ρ0,产生的浮力赝势能是
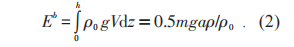
此势能并非一个真的势能,只是一个赝势能,代替了木块浸入后液体的重力势能增量。此时,总势能 E = 重力势能 + 浮力赝势能 = −mgaρ/ρ0+0.5mgaρ/ρ0,即
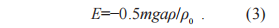
基于此,我们考虑木块在有限面积液面S0的浸入。在木块受力平衡时,下降的绝对高度是(a−V0/S0)ρ/ρ0,浮力赝势能是
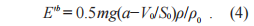
此时木块的总势能E′为
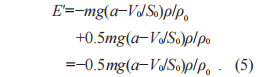
如果只考虑浮力与重力的平衡:浸入时排开液体的重量等于木块的重量,这个尺寸为a×b×L且密度为ρ的均匀长方体木块在有限大液面上的漂浮可以采取无限多种状态。如果再考虑到力矩平衡,只会有6种可能性:分别是a,b,L垂直于液面且以上或下表面为底面的方式浸入。但是,实际情况却是木块以最短的边长a垂直浸入才为稳定。这是因为(5)式中的木块总势能E′比其他4种状态都要低[5]。另外,在力平衡时的各种可能状态下,木块在有限大液体表面积的总势能比无限大液体表面积情况下的总势能多出一个恒定的增量ΔE′ [5],
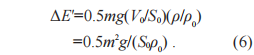
因为此增量与可能的力平衡浸入状态无关,所以无论在一个小水盆或一个大湖表面(假定水密度相同),一个木块的浸入方式是不变的。上方式(2),(3),(4)和(5)只是均匀长方体的情况。如果具有不规则形状和/或非均匀密度,则需要利用微积分,请见文献[5]及其支持信息。
验证总势能最低状态为稳定状态
作为例子,均匀立方体木(塑料)块浸入水中随相对密度ρ/ρ0转换的两种稳定状态验证了浮力赝势能的正确性、可行性与便利性[5]。由于木(塑料)块所受力与力矩的对称性要求,均匀立方体在水中的浸入方式只能有三种(图3(a)中插图):(1)Type I,立方体的4条体对角线的任一条垂直地插入水面;(2)Type II,立方体6个表面的任一表面平行于水平面浸入;(3)Type III,立方体6个表面的任一面对角线垂直插入水面。经过对包含了立方块的重力势能与浮力赝势能的总势能的大量详细计算,发现:Type III在所有的立方块与水的相对密度0—1范围内,均没有最低能量状态;Type I在相对密度为0.2246—0.7754(无理数,略写到小数点后第4位,下同)时总势能最低;Type II在相对密度为0—0.2246与0.7754—1的两个区间内总势能最低;在相对密度0.2246和0.7754时,Type I和II具有相同的总势能,都是稳定状态,如图3(b)所示;在相对密度为1时,Type I,II和III都是稳定状态[5],与日常经验相符。很多情况下,不同浸入方式的能量差别非常小,如图3(a)所示。为清楚显示这种差别,用指数函数100(E2'-E1′)/mga放大,如图3(b)所示。
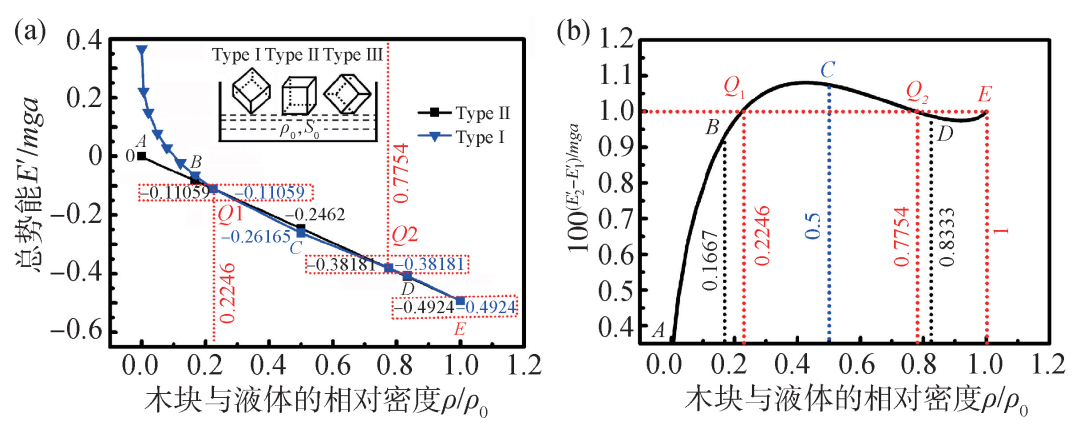
图3 因力平衡和力矩平衡的需求,不同密度的均匀立方木块(a = 2.00 cm)浸入玻璃缸水中(液面面积 S0 = 0.0263250 m2)的三种可能浸入方式及其能量计算。因Type III(面对角线垂直于水面)具有相对高的总势能,为清楚起见,此处被省略。(a)三种可能浸入方式及线性坐标下的Type I和Type II随密度变化的能量计算曲线;(b)用指数函数100(E2′- E1′)/mga放大Type I和Type II浸入方式的总势能差别[5]
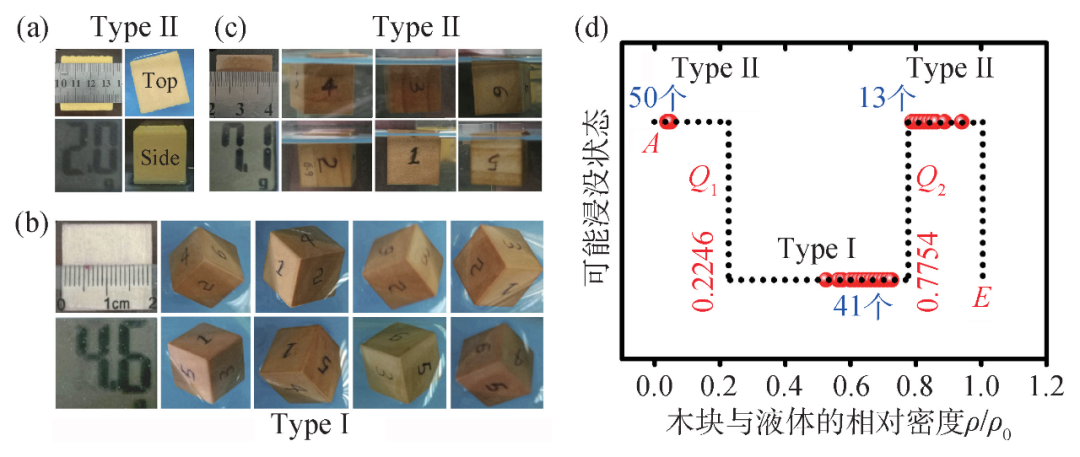
图4所示的实验对以上计算结果进行了验证。在相对密度为0.7876时(在0.7754—1区间),对应的Type I,II和III的总势能分别为−0.39306mga,−0.39380mga(最低)和−0.39217mga,差别非常微小。即使如此,实际浸入方式是Type II,具有最低能量。
结语与展望
在我国现行人教版的初中物理教科书中[7],阿基米德原理清楚地阐述了浮力的大小和方向。在现行人教版的高中物理教科书的机械能章节[8],给出了重力势能的定义,指出重力势能的系统性。在美国麻省理工学院大学物理教学中,用通常的观点讲述了阿基米德原理[9]。我们认为,非常有必要在高中(或者大学)物理教科书中给出阿基米德原理的机械能本质解释,清楚地描述固态物体与液态媒介之间的静相互作用,并且给出另外一个非常重要的“力稳定”概念,使初中物理中的似乎神来之笔得到根本性的解释,让初中物理与高中(或大学)物理在看似独立的知识点上显示出内在的联系。这样可拓宽学生的眼界,使他们融会贯通,提高他们分析问题和解决问题的能力,增加他们学习物理的兴趣。我们建议,有必要在重力势能部分或者大学物理中的流体静力学部分加入或部分加入这样的内容:“描述固态物体与液体媒介之间静态相互作用力的阿基米德原理,在有限或无限液体表面积状态下都成立;阿基米德原理所描述的浮力本质上来源于液体媒介的重力;液体媒介的重力势能可方便地由浮力赝势能代替;物体在液体媒介上的稳定状态是物体的总势能最低状态”。该液体媒介上物体稳定状态的文章不仅说明浮力和阿基米德原理的本质,介绍浮力赝势能的新概念,也可在当今能源短缺世纪对设计液体表面漂浮物[5],如蓝色能源发电机的体积重量分布[10]等提供参考。
