全世界只有3.14 % 的人关注了

爆炸吧知识

爆炸吧知识

分享冷爆有趣内容，汇集知识碎片，探究社会热点及人类秘史。让你有姿势地涨知识，拥有一个有趣的灵魂。

169篇原创内容

公众号

在现实生活中我们可以发现，那些比较容易染上赌博恶习的，通常是拥有严重侥幸心理的人。

他们往往拥有“乐观”的心态，即使十赌九输，他们也会自己说服自己，认为下一局一定可以逆风翻盘，然后就在这种自我欺骗下，酿成一个又一个的悲剧。

然而，再乐观的赌徒在实际生活中的情况也是不容乐观的。纵使他们再怎么欺骗自己，也没有办法战胜概率问题。

举个简单的例子，在一个抛硬币的游戏里面，连续投掷了10次的结果都是正面朝上，那么第十一次投掷，你认为结果如何？

答案无非就三个：第一，正面朝上；第二，反面朝上；第三，正面朝上和反面朝上的概率相同。学过概率的我们都知道，正确答案应该是第三个。但是在现实生活中，由于受到前面10次结果的影响，我们真正做出的选择会具有明显的倾向性。

选择第一种的，这种逻辑我们称之为“热手谬误”（又叫正近因效应），即某件事发生了很多次，因此可能接着再次发生。例如某位赌徒连续三次下注都赢了，他就会认为自己手气正旺，应该继续下注。

选择第二种的，我们称为“赌徒谬误”（也称蒙地卡罗谬误），即同样的事情多次发生，那么下一次发生的就应该是相反的事情。就好比如连续几天的好天气会让人担心周末下大雨，乐观的赌徒总认为自己久输必赢。

事实上，即使前面投掷了100次都是正面朝上，对第101次的结果也是没有影响的，这就是两个相互独立事件。

赌徒谬误与热手谬误其实就是忽略了某件事情前后的相互独立性，将它们在某种程度上自我相关了，从而产生的逻辑错误，让赌徒们心甘情愿地陷入自己的乐观陷阱里。

最早提出并证明大数定律的数学家雅各布·伯努利（Jakob Bernoulli‎）。

赌徒谬误的产生大多来源于人们对“大数定律”的误解。

大数定律，即在随机事件的大量重复出现中，往往呈现几乎必然的规律。通俗来讲就是，在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。

例如抛硬币的次数足够多时，我们会发现正面或反面朝上的结果都会接近一半。

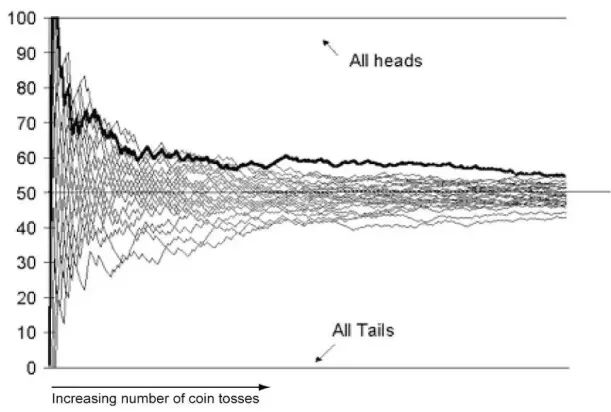
然而，人们会错误地诠释大数定律的“平均律”，认为事情的随机发生就意味着均匀。例如在赌博中，连输几盘后，赌徒就会认为事件应该往“抹平”的方向走，觉得下一局的赢面会更大。

事实上，大数定律的平均律并不是这样用的，它的工作机制并不是为了平衡过去已发生的事情或者与之对抗的。

更何况大数定律只适用于重复发生次数足够多的情况，一般赌徒哪来钱输这么多次？

既然每次输赢概率都一样，都是“全新的开始”，那赌徒们可就重整旗鼓要准备翻盘了！

别急，别急，出来赌迟早是要输光的！

这里就涉及到了一个“无限财富理论”，即哪怕赌场不出千，玩家输赢概率确实是五五开的情况下，只要玩家手中的财富没有超过赌场的财富，那么一直赌下去只会越输越多。

早在18世纪初，就有一群热爱赌博的概率论数学家们提出了“赌徒破产定理（Gambler’s ruin）”，即在“公平”的赌博中，任何一个拥有有限赌本的赌徒，只要长期赌下去，必然有一天会输个精光。

我们假设赌徒的初始资金是n，每赌一次或输或赢，资金分别变为n-1和n+1。输或者赢的概率为0.5，那么一直赌下去，资金变为0的概率是多少？

假设从n开始一直赌下去变为0的概率是p(n)。

那么我们有：

p(0)=1

p(n)=0.5*p(n-1)+0.5*p(n+1);

p(n)=(p(n-1)+p(n+1))/2,对n>0.

第二个式子相当于数n有一半机会变成n-1，一半机会变成n+1。

那么变换一下就相当于p(n+1)=2p(n)-p(n-1)。

设p(1)的值为a,那么显然0<a<=1。利用p(n+1)=2p(n)-p(n-1),则

p(1)=a

p(2)=2a-1

p(3)=2(2a-1)-a=3a-2

p(4)=4a-3

…

p(n)=na-n+1。

我们知道p(n)>=0对于任意的n成立。

在n(a-1)+1这种情况下，a无限接近1，所以我们证明了p(1)约等于1。同样的过程可以得到p(2)约等于1,…，

一直下去，p(n)约等于1。

也就是赌徒资金变为0的概率为1。

由此，可以得出一个违背直觉的结论：只要你的财富不是无限的，以50%的概率赌下去，必然会全盘皆输。

传说香港马会靠的就是这一招，不作弊不抽成，轻轻松松地赚走了无数赌徒的“全副身家”。

更何况现实中赌场大都是“十赌九骗”呢？赌场要想来钱快，必定会在赌场中进行一些对自己有利的赌局，概率也未必会设置在公平的50%。

所以，资金本就有限、脑袋又不如那群赌徒数学家灵光的人，何以去和大资本家们抗衡？去赌场不就相当于带着全副身家自投罗网吗？

即便是在民间广为流传的“必胜法则”，也躲不掉这样的陷阱。

举个例子，在猜大小的赌局中，玩家下注后，要么开大要么开小。如果输了就输去赌注，赢了就可以获得原赌注一倍的利润。

具体操作如下：

第一把下注100押大，输了；

第二把下注200押大，输了；

第三把下注400押大，输了；

第四把下注800押大……

从概率上来看，只要赌的次数够多，就不会一直开小。

那么这样赌下去，总会有赢的一局，不仅能把之前输掉的赌本都赢回来，还能额外收获100的利润。怎么看这都是一个能赢钱的策略。

但现实真的就这么简单吗？事实上，所谓的“必胜法则”无非就是早在18世纪就流行过了的“加倍赌注法（martingale）”。

就算流传了好几个世纪，你见有哪位赌徒凭借这个法则笑到最后了吗？

加倍赌注法只是看上去“必胜”，实际上越到后面风险越大。

你不知道你要赌到哪一把才能赢，况且即使赢了，但赌注已经高达成百上千亿，最后能赢回来的不过是最初的赌本外加100块，与所承受的风险完全不成比例。

而以指数增长的赌金，最终会让资本有限的赌徒坠入破产的深渊。

或许你听说过棋盘摆麦粒的故事吗？

麦粒的数量每格倍增，要想放满64格，全世界用500年也种不出这么多麦子。

网上的各种时时彩也很喜欢用一些“倍投法”来将赌徒哄骗入坑。

这种骗局的倍投法并不局限于“双倍投”，还推出了各种“倍投”来增加所谓的赢面。

概不例外的是，这种骗局只要挂一次，就很容易再无翻身之日。

道理人人都懂，可有些赌徒就是控制不住自己的手和侥幸心理，总有办法自我催眠，认为破产的不会是自己。

但赌就是赌，赢了的还想赢，输了的就想翻盘。这人一旦上了赌桌，不管身家大小赌术高低，不赌到倾家荡产，谁也别想收手。

赌博，赌的从来就不是概率，而是人性的贪婪。

少年数学家

连接三角形顶点和对边中点，并无限重复，最终会得到什么？#三角形重心#好玩的数学

视频号

 限时福利  

任何订单问题，咨询在线客服👇

数学好物

严选全球数学文化、思维训练、新科技生活好物！

6篇原创内容

公众号