美术馆定理回顾

先来简单回顾一下美术馆定理（Art Gallery Theorem）：

美术馆定理是说最少只需  名保安便可监视任意一个形状为  边形的美术馆，其中  表示不超过  的最大整数，这里的保安有  视野，可以位于  边形任意位置，包括顶点和边线，并且始终保持原地位置。

红点处设置保安可监视全部区域

定理实际分为必要性和充分性两方面。

必要性是指存在一种  边形的美术馆，至少需要  名保安才能监视全部区域。我们构造了“梳子”形的美术馆满足这一要求，从而完成了必要性的证明。

充分性是指对所有N边形的美术馆，至多需要  名保安就能监视全部区域。数学家Steve Fisk给出了非常精彩的证明，分为三步：

从而完成了充分性的证明。

3-染色后数量最少的红色点处设置保安即可

直角多边形美术馆定理

更多情况下我们遇到的建筑都是直角  边形的形状，即相邻两面墙壁是互相垂直的，虽然  个保安对直角  边形也总是够用的，考虑到人力成本很贵，那还能不能更少点人呢？

答案是肯定的，事实上，三名数学家Kahn、Klawe和Kleitman于1980年证明了最少只需  名保安便可监视任意一个形状为直角N边形的美术馆！

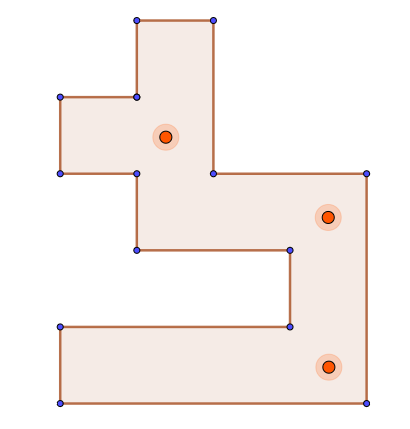
3名保安一定能无死角监视直角14边形的美术馆

同样的，我们分别从必要性和充分性两方面来证明这个定理。

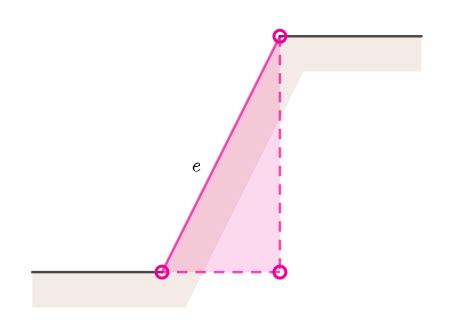
必要性：存在一种直角N边形的美术馆，至少需要  名保安才能监视全部区域。

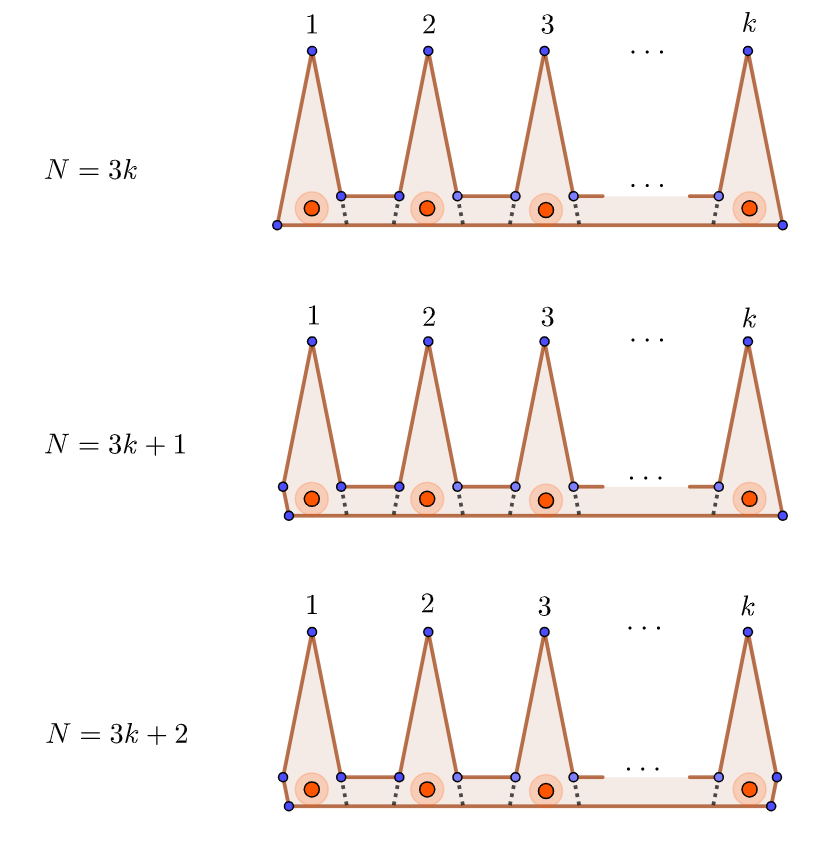
仿照一般多边形的尖齿“梳子”形构造，我们可以构造平齿“梳子”来解决必要性，如下图：

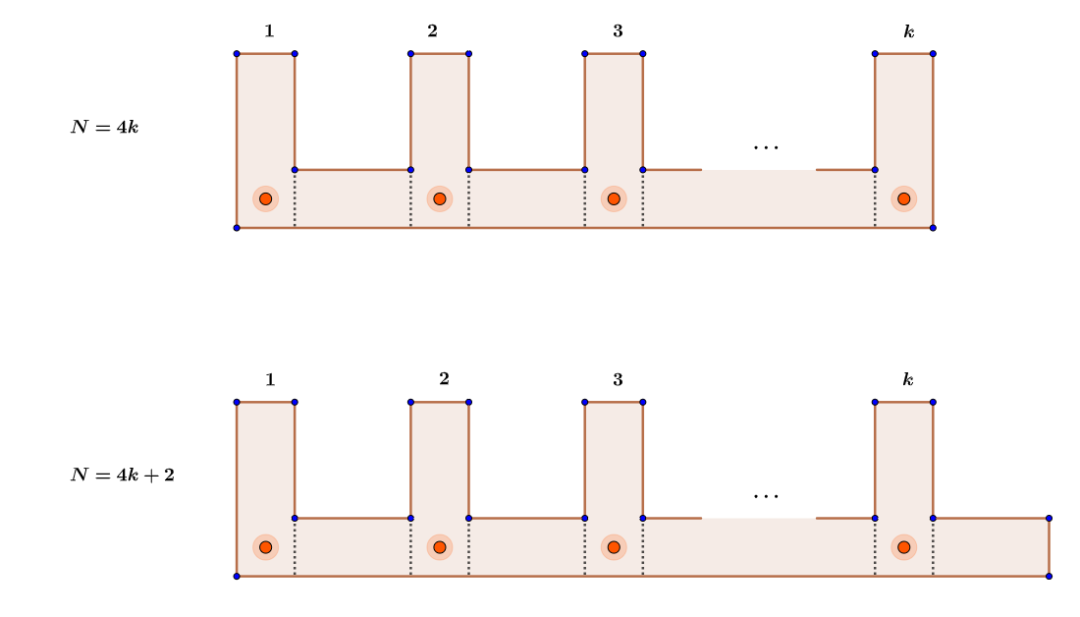
平齿梳子型直角N边形的美术馆至少需要  名保安

这里注意到对于直角  边形，  总是偶数（想想这是为什么？）。

充分性：对所有直角N边形的美术馆，至多需要  名保安就能监视全部区域。

这是整个定理比较复杂的部分，不过我相信同学们通过勤加思考是一定可以攻克的。

下面我们来看充分性的证明，该证明来自于加拿大女计算机学家Anna Lubiw：

与一般  边形美术馆定理充分性的证明非常类似，该证明的核心也主要在于如何将直角  边形剖分为若干个凸四边形。

因为在凸四边形任一顶点设置保安，可以监视整个四边形区域，而凹四边形则不然。于是如果我们能给直角  边形的顶点染色，使得每个凸四边形的四个顶点颜色都不相同（称之为  -染色），那么在数量最少的那种颜色的顶点上设置保安，即可监视整个区域，从而保安人数  。

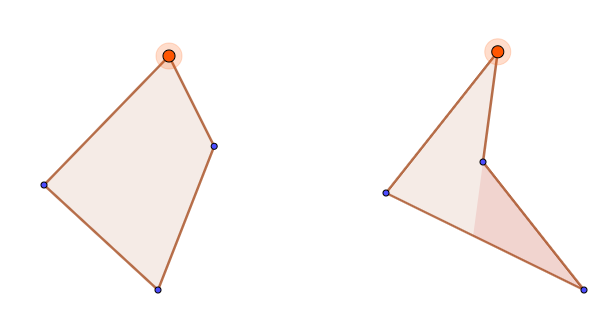
1个保安并不总能监视整个凹四边形区域

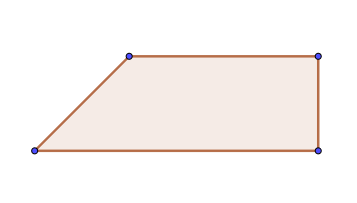
我们允许退化的凸四边形（即内角可以是零角或者平角）存在，如下图：

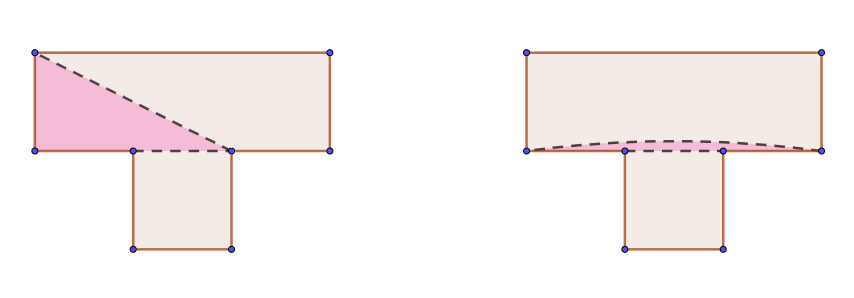
红色区域是退化的凸四边形（右图作了变形处理）

但凸四边形剖分并不总是能实现的，比如下面这个多边形就不行。

不能剖分成若干个凸四边形

Lubiw很敏锐地发现了一大类可以进行凸四边形剖分的多边形，而直角多边形正是这类多边形的特殊情况，从而完成直角多边形的凸四边形剖分工作。

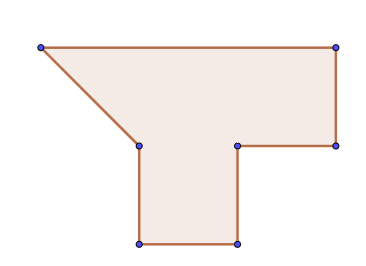
她发现的这类可凸四边形剖分的N边形满足以下条件：

红色区域为  的阴影（不含顶点和虚线部分）

我们称满足上面四个条件的多边形为伪直角N边形。如果上述四条中的任何一条不满足，都存在让凸四边形剖分失败的反例。

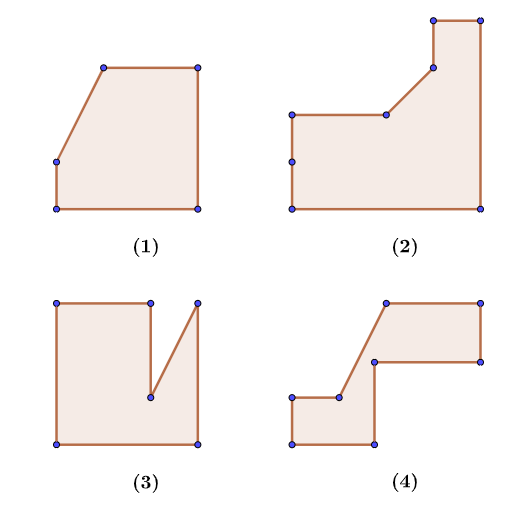
图1、2、3、4分别不满足伪直角多边形对应的四个条件

伪直角  边形必能被凸四边形剖分

下面给出伪直角  边形能被凸四边形剖分的证明，不感兴趣的读者可以略过这部分，不影响文章整体阅读。

我们采用数学归纳法来证明。

  时，伪直角四边形只有下面这一种（不考虑旋转/反射导致的差异），归纳基础成立。

假设任意边数少于  的伪直角多边形都可以进行凸四边形分割，下面来证明当  时，我们可以通过去除一个凸四边形将伪直角  边形分割成若干个边数更少的伪直角多边形，从而完成归纳递推。

由伪直角N边形条件1和2知，与斜边  相邻的边只能同时水平或同时竖直。结合条件3，我们得到伪直角  边形只有以下两种类型（不考虑旋转/反射导致的差异）：

  两点就是我们要去除的凸四边形的两个顶点，现在来找另两个点  和  。

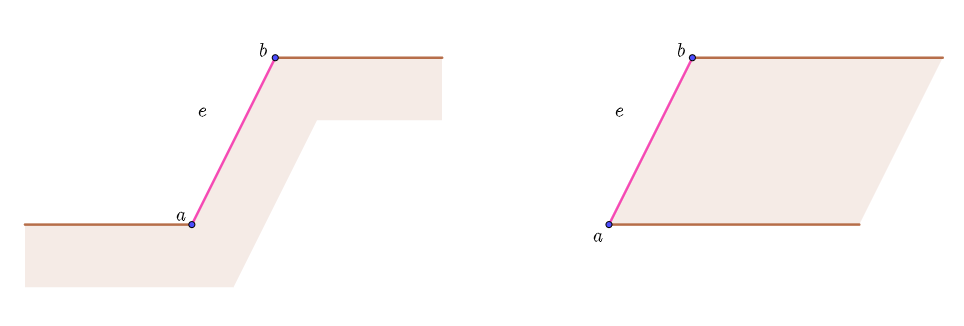
对于  ，如下图所示作出区域  （含上边界和左边界，不含下边界和左边两顶点），找到区域中最靠左的顶点中最上端的点作为  ，由于  至少包含上边界的右端点（左端点为  ），因此  点总是存在的。

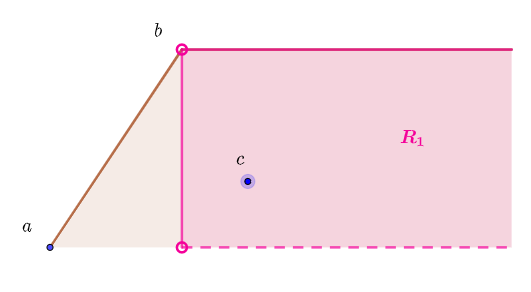
由c的作法我们可知，它们之间的相对关系只有以下三种：

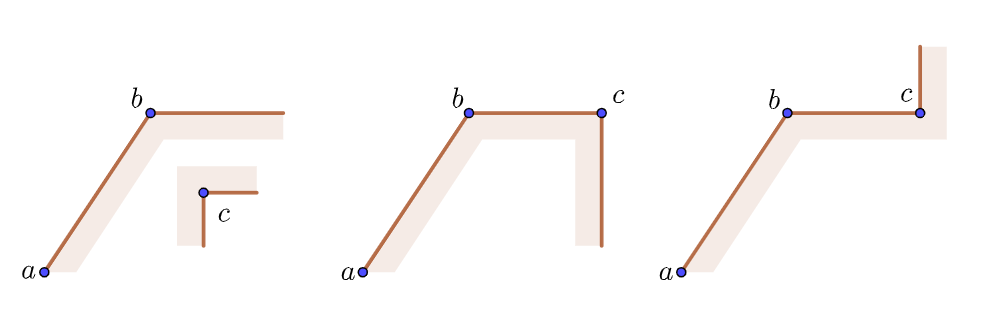
对于点  ，如下图所示以  为上边界作出区域  (含上和右边界，不含左边界和上部两顶点，即  和  )，找到区域中最靠上的顶点中最右端的点作为  。

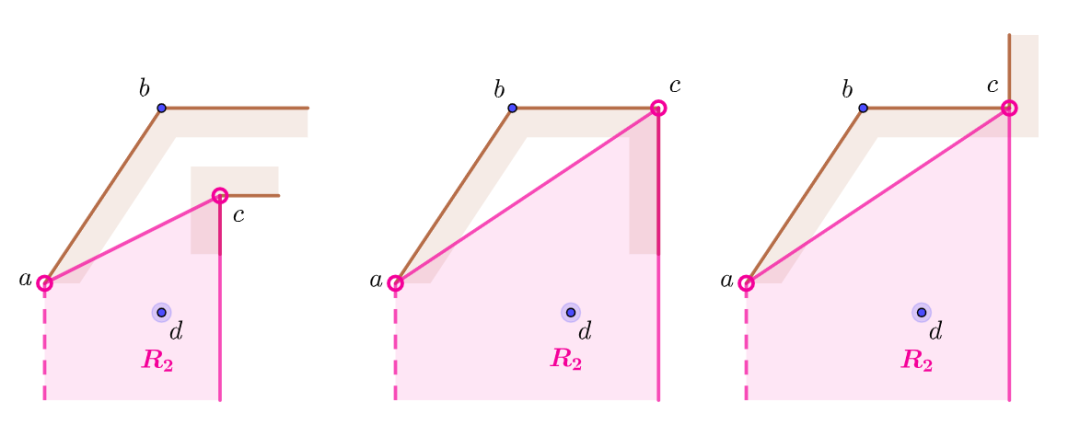
对于上图中的前两种相对关系，  至少包含右边界的下端点（上端点为  ），因此这两种情况下  总是存在的。对于第三种相对关系，  可能不存在，或者虽然存在，但是是某条水平边的左端点。这两种情况下我们需要重新画区域来寻找  点。

左图选出的d点要舍弃重选，右图不存在符合的d点

如下图所示作出区域  （含左和下边界，不含上边界和左边两顶点），找到区域中最靠左的顶点中最下端的点作为  。由于  至少包含下边界的右端点（左端点位于  内或  的左侧），因此  总是存在的。

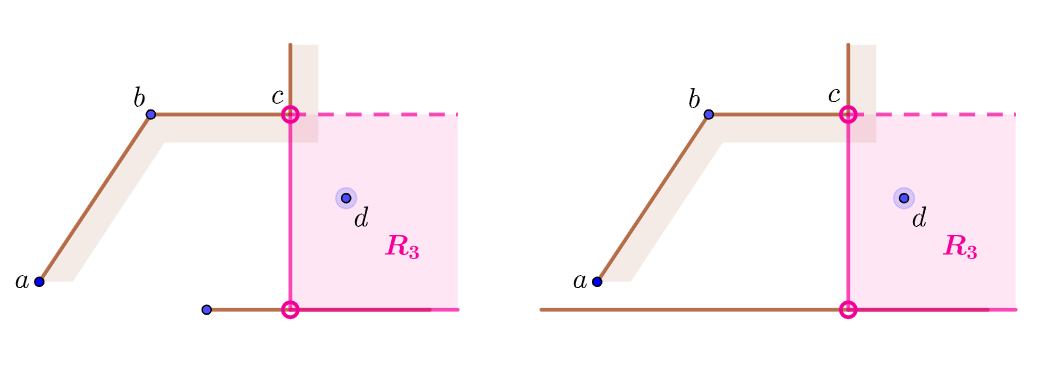
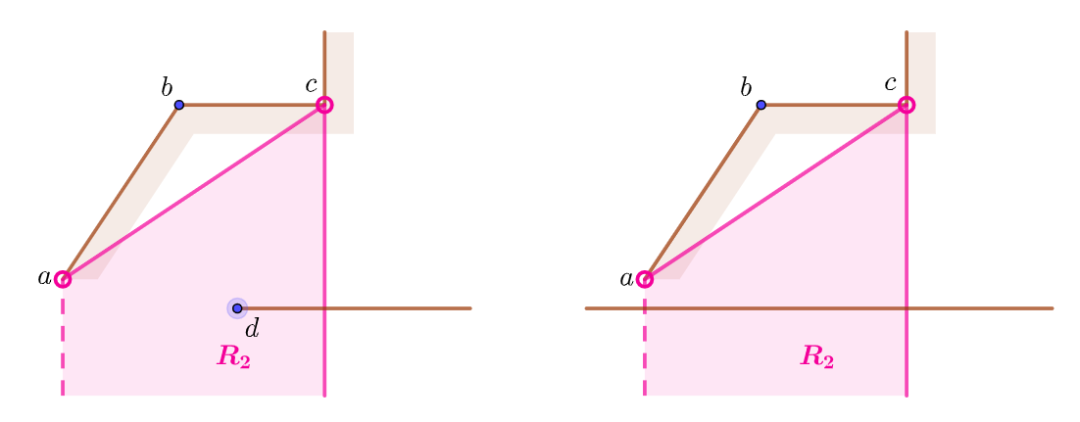
重新选取的d点

至此，四个顶点  都已选出，我们首先需要说明四边形  是凸的。因  和  都在直线  的同侧，故点  和  都是凸的，而  和  也在直线  的同侧，故点  和  也是凸的，从而  为凸四边形。

根据不同条件下点  和  的选取，被去除的凸四边形  只能分为以下五类，如下图所示。

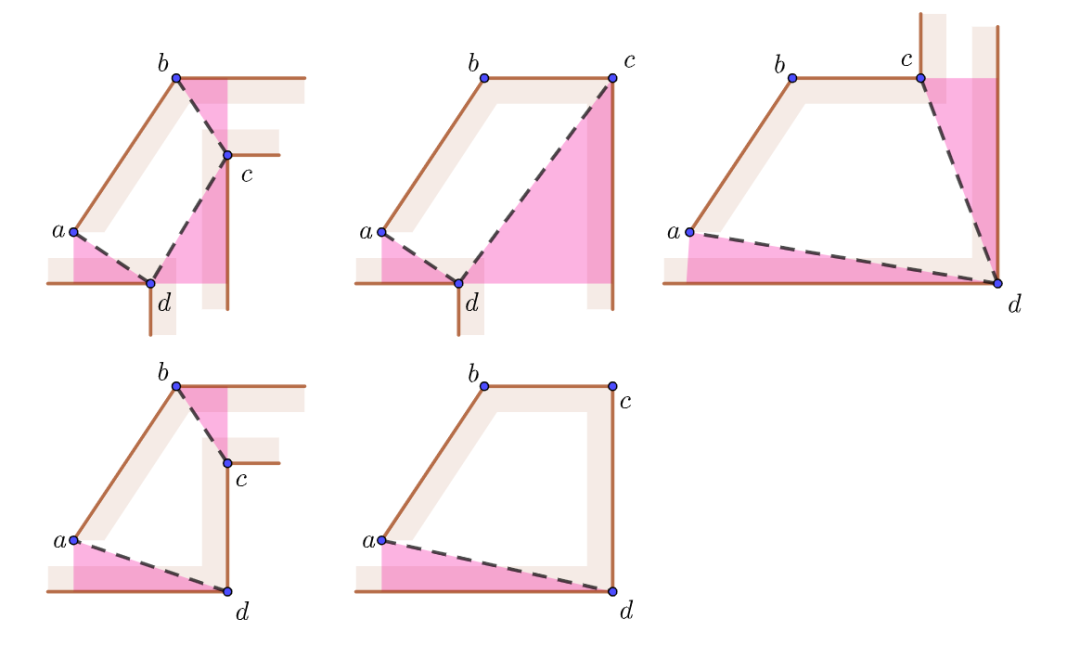
红色区域是对角线的阴影

容易看出，去除凸四边形  后，原伪直角  边形被分割成不多于三个边数更少的多边形，那它们都是伪直角多边形吗？我们需要用伪直角多边形的四个条件来判断。条件2是显然满足的，条件3和4也可以在上面五类情况中得到验证。

稍微麻烦点的是条件1，如何证明分割成的多边形边数都为偶数呢？

Lubiw给出了一个非常聪明的办法，将原伪直角  边形的  个顶点分成两类进行标记，其中上边界的右端点、下边界的左端点、左边界的下端点以及右边界的上端点标记为  ，上边界的左端点、下边界的右端点、左边界的上端点以及右边界的下端点标记为  ，从而标记为  和  的顶点交替相邻。

从被去除的凸四边形  的五类情况中可以看出，  只能为  ，  只能为  。因此对角线  都是一个  和一个  相连，从而被分割成的多边形也是  交错，故边数为偶数。

这样我们就证明了伪直角  边形去除凸四边形  之后，被分割成若干个边数更少的伪直角多边形。而由归纳假设即得任意伪直角  边形都可以进行凸四边形剖分。

如果斜边  为水平或竖直，则伪直角  边形退化为直角  边形。所以任意直角N边形都可以进行凸四边形剖分。

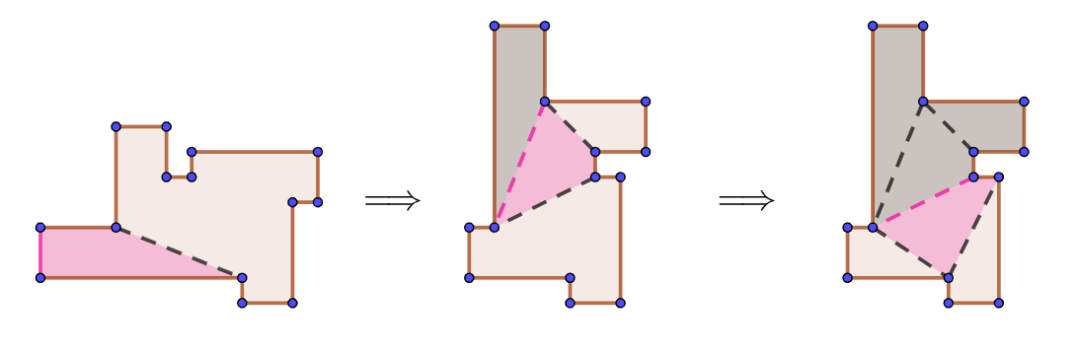
直角多边形凸四边形剖分的例子

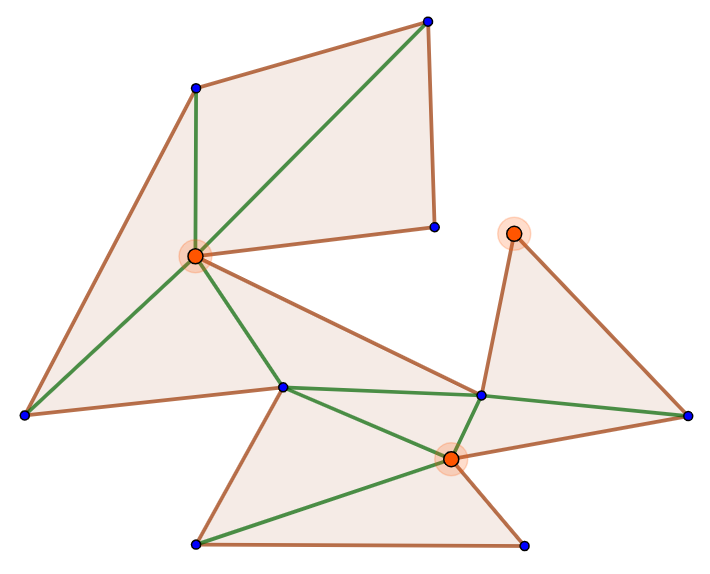
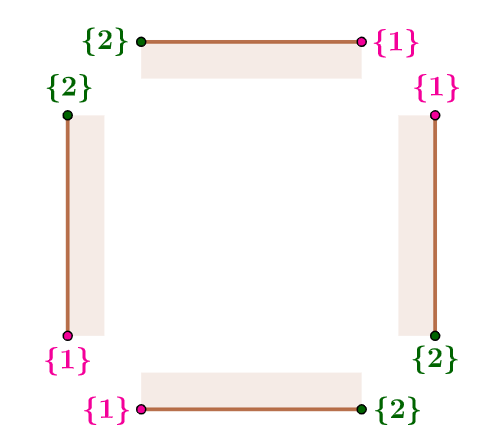
顶点染色

完成了直角  边形的凸四边形剖分，现在如果我们能给直角  边形的顶点染色，使得每个凸四边形的四个顶点颜色都不相同（称之为  -染色），那么在数量最少的那种颜色的顶点上设置保安，即可监视整个区域，从而保安人数  。

这种凸四边形剖分的多边形一定可以按这种方式染色吗？我们可以通过数学归纳法来证明！

  时，显然可以  -染色。

假设任意边数少于  的凸四边形剖分图都能被  -染色，下面来证明当边数为  时  -染色仍能进行，从而完成归纳递推。

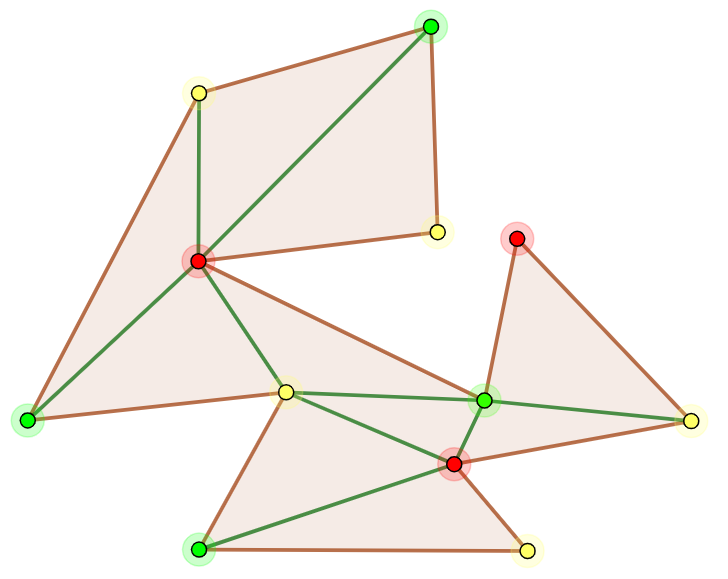
将每个凸四边形视作一个点，两个凸四边形相邻则用连接两点的线段表示，这样我们就作出了凸四边形剖分后的直角N 边形的对偶图。

如果一个图形中任意两个节点间有且只有一条路径，我们称之为树。容易看出对偶图是树，否则图中必存在一环路，对应到原图中则形成多边形中的一个孔洞，与我们研究的直角多边形不符。

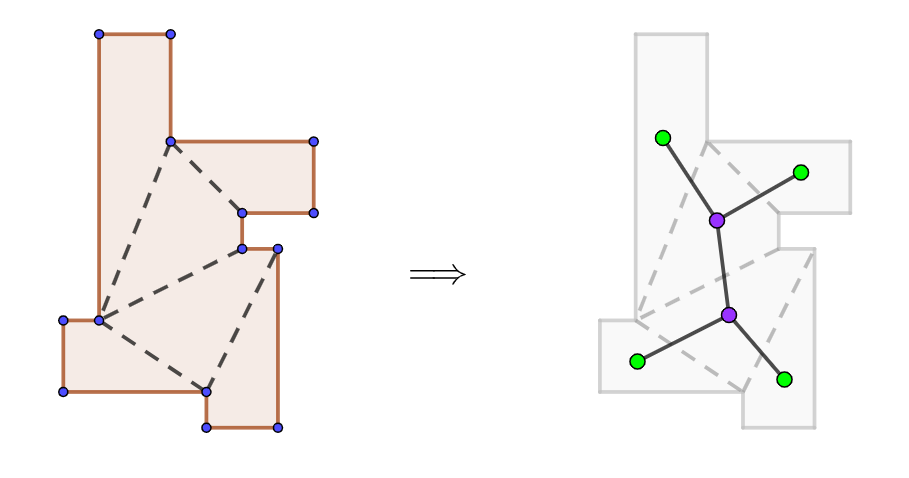
凸四边形剖分的对偶树图，绿色为树叶节点

对于树，一定存在只连接一条边的节点，我们称该节点为树叶。树叶对应到原图则为一个由三条边和一个对角线构成的凸四边形。沿对角线裁剪下该凸四边形，得到仍为凸四边形剖分的多边形，但边数更少，由归纳假设，该图形可进行  -染色，我们只需将剪下的凸四边形拼回去，并将两个非对角线上的点赋予另外两种颜色即可。

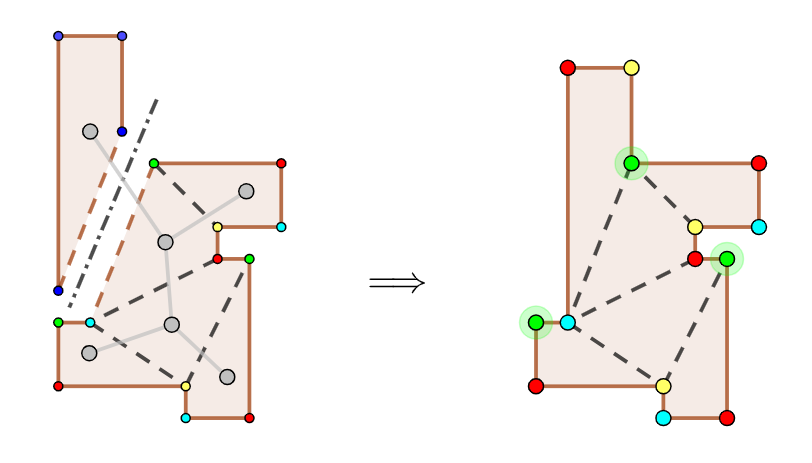
数量最少的那种颜色的顶点上设置保安即可

至此，直角多边形的美术馆定理证明已全部完成。

以上就是今天要介绍的内容，同学们学会了吗？

参考资料：

1. Lubiw A. Decomposing polygonal regions into convex quadrilaterals[C]. Proceedings of the first annual symposium on Computational geometry. 1985: 97-106.

2. O'Rourke J . Art Gallery Theorems and Algorithms[M]. Oxford University Press， Inc. 1987.

作者：大神团·冯伟

作者介绍：冯伟，新东方智慧学堂授课老师，清华大学材料科学与工程硕士，清华大学优秀硕士毕业生。

来源：新东方智慧学堂

编辑：aloysius

近期热门文章Top10

7. 你绝对想不到，心脏其实并不是心形……

8. 被神曲洗脑了！怎样才能停下来？

9. 笛卡尔，不行！黎曼，行！