工频信号干扰

问题描述

如何有效地提高传感器的测试精度是行业的发展趋势；近来，对传感器进行实验测试过程中发现结果存在明显的工频干扰，信号中夹杂有明显噪音，具体频率为50hz，因此，近来以解决实际问题为出发点，对相关的内容进行归纳汇总；目前，消除噪音，提高传感器采集精度主要包含两种手段：1、硬件：通过电阻电容及电感构成滤波电路，对外界干扰源进行屏蔽；2、算法：通过数字信号处理，构建IIR、FIR滤波器对噪声信号进行滤除；具体内容如下所示~

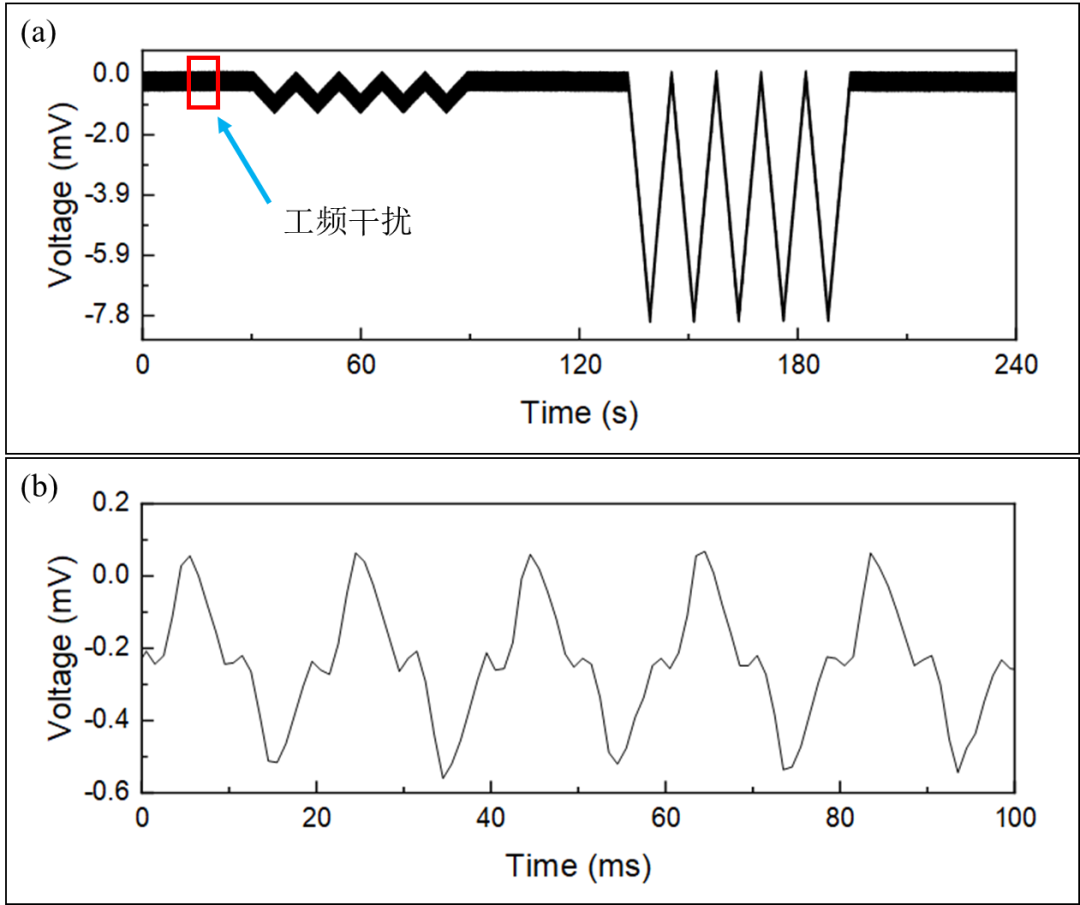
图a表述为信号采集系统实际测试结果，源信号中包含工频干扰，即使传感器未发生变形，输出信号具有明显的波动（幅度为0.6mv左右）；图b表述为局部放大示意图，从图中可以看出干扰源的频率为50hz。

附录：补充材料

附1、硬件如何实现信号滤波？

本部分从硬件的角度对信号滤波整体方案进行介绍，主要分为三方面内容：1、滤波器的种类以及相关电路，推导了二阶低通、高通滤波器的传递函数（实际中应用最广）；2、带通以及带阻滤波器具体结构；3、带通滤波器具体设计过程，分享了MATLAB程序；

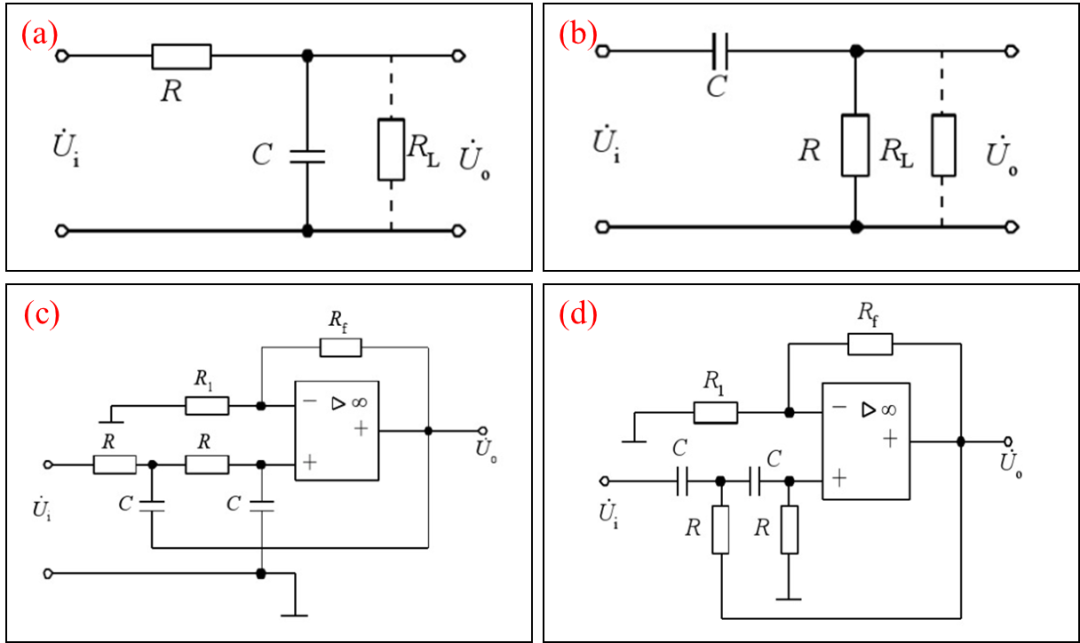
图a表述为无源一阶低通滤波器基本结构；图b表述为无源一阶高通滤波器基本结构；图c表述为压控性二阶有源低通滤波器基本结构（现实中应用较广），第一阶电容C直接与运算放大器输出端连接，引入正反馈，能够有效地减小信号干扰；图d表述为有源二阶高通滤波器基本结构；

附1：无源滤波器具有的优点为：电路简单，可靠性高；相应的弊端为：信号经过滤波器后具有能量损失；具有明显的负载效应；信号无放大作用等；附2：同相放大器具有输入阻抗高，输出阻抗低的特性，广泛应用于前置放大级；附3：Rf电阻值不能大约2倍R1电阻值；

本部分对现实中应用最为广泛的有源二阶滤波器进行分析，其中，低通滤波器的传递函数为：

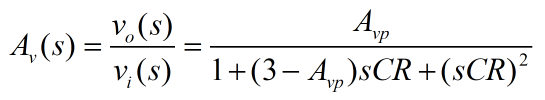
通带增益为：

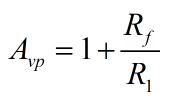
高通滤波器的传递函数为：

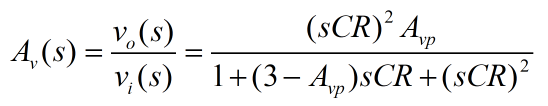
通带增益为：

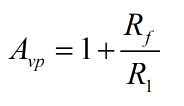
另一方面，带通、带阻滤波器可以通过基本的低通、高通滤波器串并联组成，其基本结构为：

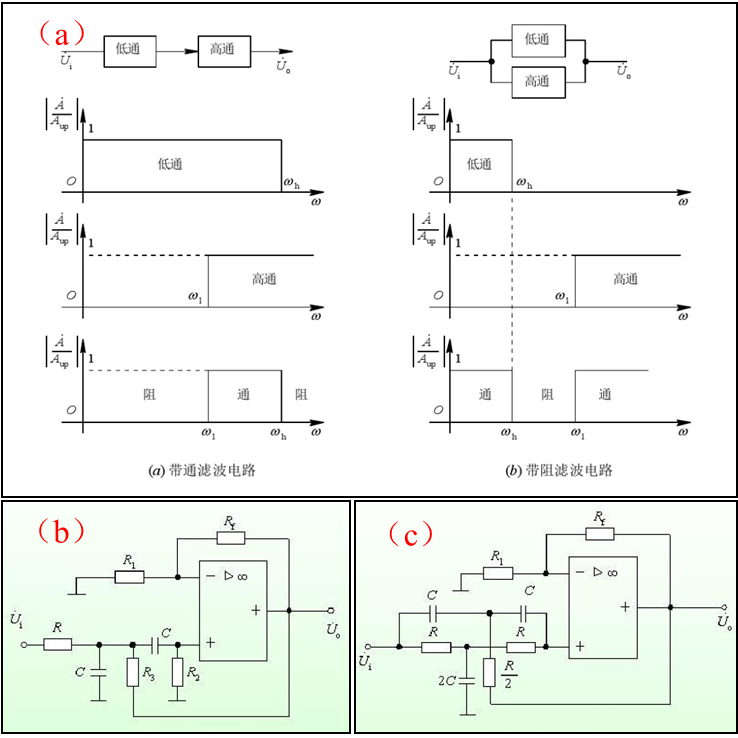
图a表述为低通滤波和高通滤波器串并联组成带通、带阻滤波器的基本过程；图b表述为带通滤波器基本结构；图c表述为带阻滤波器基本结构；

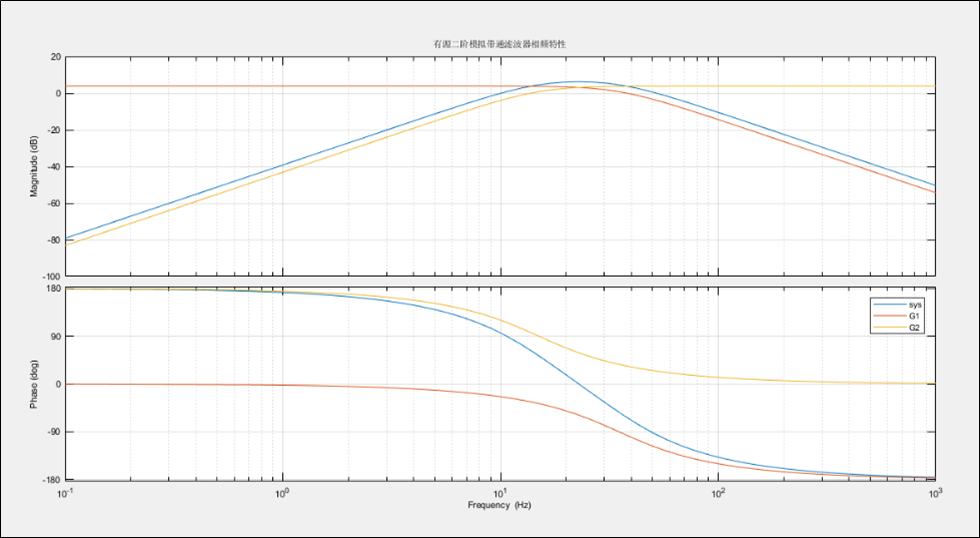
上图表述基于MATLAB进行带通滤波器设计的具体过程，程序源代码如下所示，图中三条曲线分别代表低通滤波器、高通滤波器以及串联组成带通滤波器的幅频曲线，相关结果通过bode图进行直观展示，其中，纵坐标的单位为dB（20lg|G(jw)|），横坐标采用对数坐标系；附1：20dB表示信号衰减一个数量级；附2：硬件电路设计过程中，相关电阻的大小通过下述程序确定；

clear all;clc%有源带通滤波器%LPF 传递函数计算 f0=35Hz C = 1uF，R = R=4.549kΩ c1 = 1e-6;r1 = 4549;%HPF 传递函数计算 f0=15Hz C = 1uFc2 = 1e-6;r2 = 10615;%q 品质因子（品质因子和通带增益具有一定关系）q=0.7%LPFAvp1 = 3-(1/q);k1 = (3-Avp1)/(c1*r1);k2 = 1/(c1*c1*r1*r1);k3 = Avp1/(c1*c1*r1*r1);num1=[k3]; %传递函数分子den1=[1 k1 k2]; %传递函数分母G1=tf(num1,den1);%HPFAvp2 = 3-(1/q);k4 = (3-Avp2)/(c2*r2);k5 = 1/(c2*c2*r2*r2);k6 = Avp2;num2=[k6 0 0]; %传递函数分子den2=[1 k4 k5]; %传递函数分母G2=tf(num2,den2);p=bodeoptions;p.FreqUnits='Hz';p.Grid= 'on';[num,den] = series(num1,den1,num2,den2); %计算串联传递函数printsys(num,den) %显示串联后的总传递函数hold on;bode(num,den,p); %绘制波特图% hold on;% bode(G1,p);% hold on;% bode(G2,p);title('有源二阶模拟带通滤波器相频特性'); %标题

附2、程序如何实现滤波？

本部分从算法的角度论述信号滤波的具体工作流程，主要的内容包含：1、滤波器具体的结构以及相关的参数设置，采样定理的含义；2、算法滤波后具体效果展示；具体内容如下~

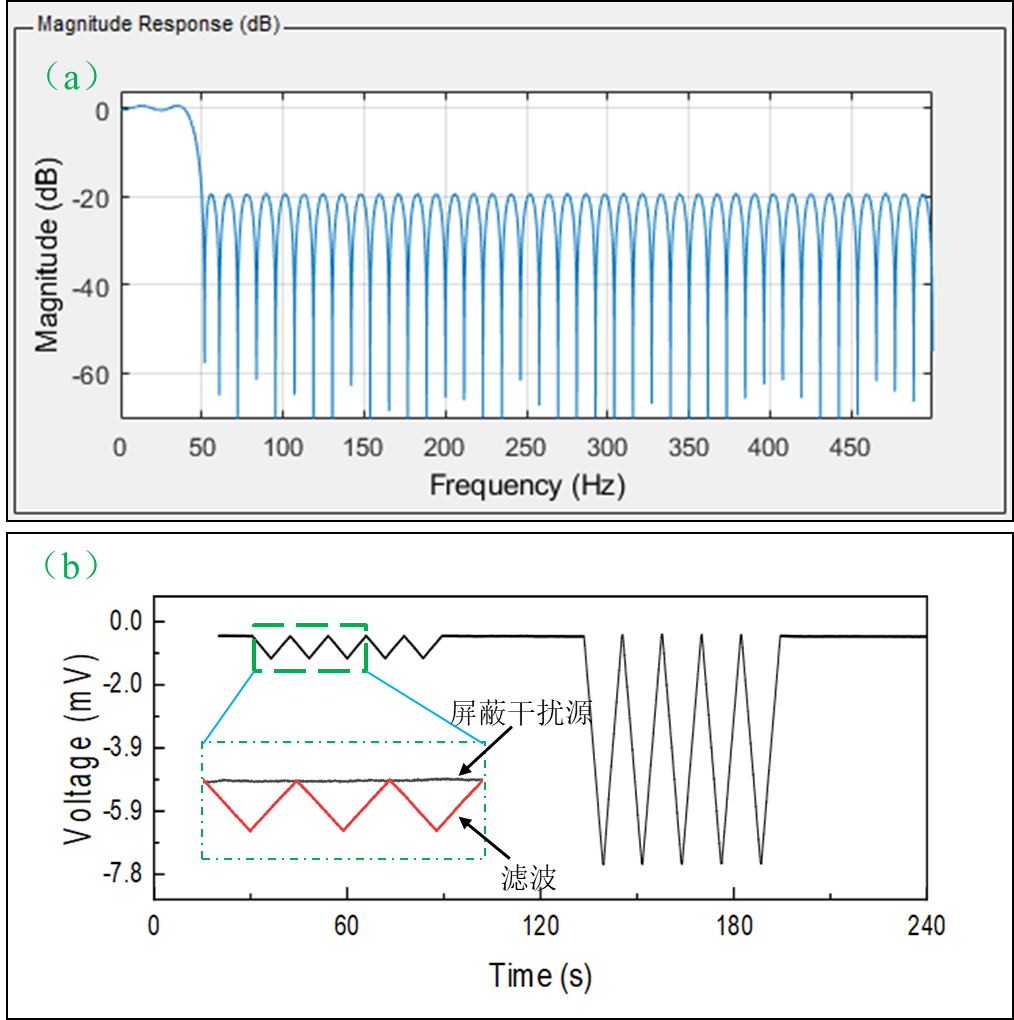
图a表述FIR滤波器的幅频特性曲线，其中，信号的采样频率为1000hz（采样定理：采样频率大于信号最高频率的2倍，即：现有测量系统在保证精度的情况下，待测信号的最大频率为500hz）；现采用低通滤波器，截止频率为50hz，当信号频率高于截止频率时，信号幅值衰减10倍以上；图b表述为采用滤波器对包含工频干扰的信号进行分析处理的结果，从图中可以看出，采用滤波算法与直接屏蔽干扰源具有相同的采样效果，还是挺不错的~

clear all;clc% 读取传感器输出信号node='信号采集结果.txt';[x,y]...    =textread(node,'%f%f','emptyvalue',0,'headerlines',10);
output=filter(lowpass,y);caiji=1000:1:length(y);output=output(caiji,1);plot(output)
function Hd = lowpass%LOWPASS Returns a discrete-time filter object.
% All frequency values are in Hz.Fs = 2000;  % Sampling FrequencyFpass = 40;              % Passband FrequencyFstop = 50;              % Stopband FrequencyDpass = 0.057501127785;  % Passband RippleDstop = 0.1;             % Stopband Attenuationdens  = 20;              % Density Factor
% Calculate the order from the parameters using FIRPMORD.[N, Fo, Ao, W] = firpmord([Fpass, Fstop]/(Fs/2), [1 0], [Dpass, Dstop]);
% Calculate the coefficients using the FIRPM function.b  = firpm(N, Fo, Ao, W, {dens});Hd = dfilt.dffir(b);% [EOF]

从本科以来，数字信号处理作为最喜欢的一门课，没想到还有派上用场的一天，😄~

免责声明：本文版权归原作者所有。本文所用视频、图片、文字如涉及作品版权问题，请第一时间告知，我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容！本文内容为原作者观点，并不代表本公众号赞同其观点和对其真实性负责。

为您发布产品，请点击“阅读原文”

阅读原文