IEEE TPAMI | 基于标注偏差估计的实例相关PU学习
以下文章来源于京东探索研究院 ,作者京东探索研究院
京东探索研究院官方公众号,我们坚持从基础理论研究出发,实现变革性创新。探索,敬畏浩瀚;未来,未曾到来!


一、研究背景
近年来,以“仅基于一组正类和未标注的训练数据集找到合适分类器”为目标的PU学习一经提出便激起了人们对它的研究热潮[1,2,3,4,5,6,7]。PU学习是一种弱监督学习方法,它的每个未标注数据集的类别既有可能是正的也有可能是负的,但真实标签在训练时未知。到目前为止,PU学习已经在视频异常检测、疾病基因识别、高光谱图像分类等各个领域得到了广泛的应用。
。然而,在实际标注过程中往往会存在标注偏差[15,16]。例如,医生在医疗诊断中更倾向于标注他们对结果有把握的CT图像,而一般的标注者更喜欢在众多场景中标注他们熟悉的对象。也就是说,PU学习中的正类数据不应该以相同的概率 被标注,一个正类样本是否会被标注不仅取决于它的标签值y,还取决于它的特征向量 ,在数学上描述为 且 ,其中 是与 相关的变量。因此,本文旨在研究实例相关PU学习,即对正类数据存在标注偏差。
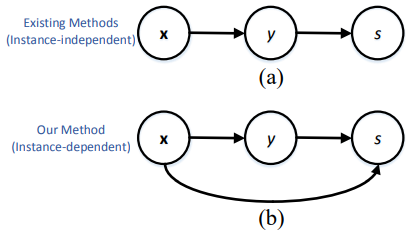 图1 本文中的PU学习方法与现有的方法比较。(a)为现有的实例无关PU学习方法,(b)为本文中的实例相关PU学习方法。
图1 本文中的PU学习方法与现有的方法比较。(a)为现有的实例无关PU学习方法,(b)为本文中的实例相关PU学习方法。由于实例相关PU学习中 依赖于 ,因此本文的实例相关方法中的概率估计比图1(a)所示传统的实例无关方法中的概率估计要困难得多。对传统的实例无关方法来说,如果 是一个常数且与 无关,则可以得到
其中 和 可以直接从数据中估计出来。然而,若是像本文所描述的那样,如果对每个 都有自己的 ,则有
从中我们观察到 与后验概率 同时出现。因此,我们需要找到一种新的方法来联合估计这两个概率。
二、方法原理简述
为了解决上述问题,本文通过建模分析提出了一种名为“标注偏差估计”(LBE)的概率方法。在LBE方法中,明确建立了输入特征向量 、真实标签值 和变量 (研究背景中已作定义,表示 是否被标注)之间的关系(见图1(b))。并且,每个训练数据都由三元组( ,,)表示,因此由n个训练数据构成的训练数据集可以表示为
其中 是大小为k的正类数据集, 是大小为 的未标注数据集。根据上面的定义,对于 ,有 ;对于 ,有 ,。而我们的目标就是在S上找到一个合适的score函数 ,这样利用函数h就可以给未被标注的测试数据 分配正确的标签值 。
1. 模型构建
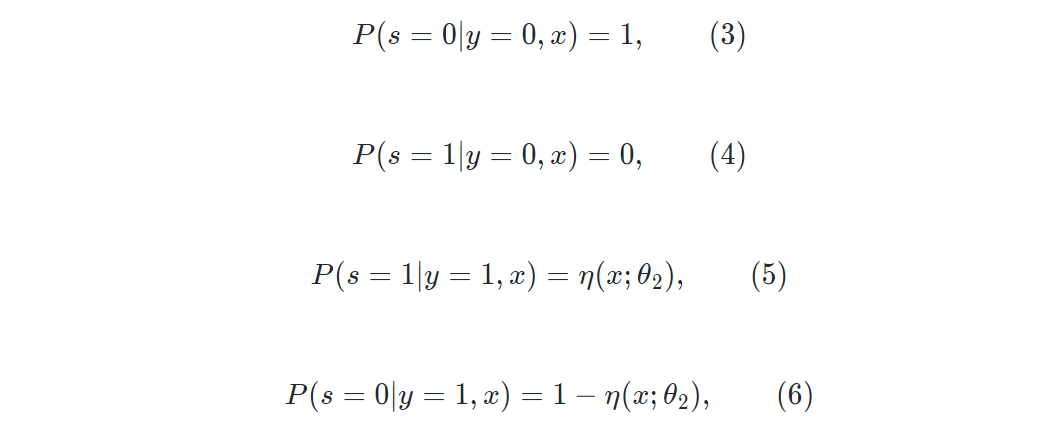
2. 参数训练
1. 远离潜在的理想决策边界的正类数据更有可能被标注;
2. 接近潜在的理想决策边界的正类数据更有可能被标注。
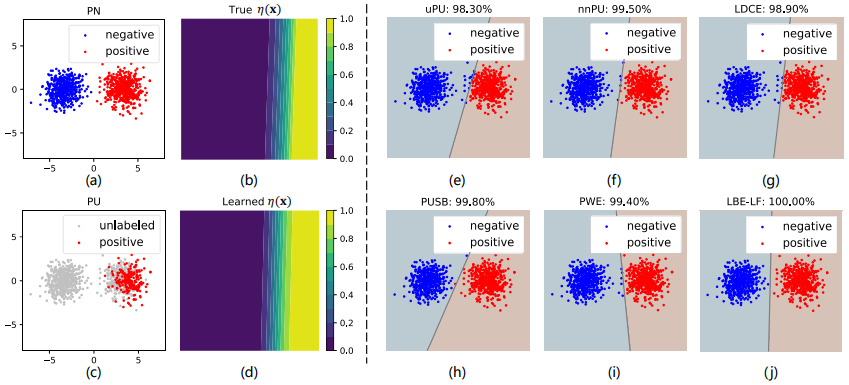 图2 策略1下各种方法在合成数据集上的表现。(a)显示了真实的正负类数据;©显示了用于模型训练的未标注数据和有标注偏差的正类数据;(b)和(d)表示真实的 和LBE-LF估计的 ;(e)-(j)显示了uPU、nnPU、LDCE、PUSB、PWE和LBE-LF生成的分类结果。每种方法的分类准确率都显示在相应的子图上方。
图2 策略1下各种方法在合成数据集上的表现。(a)显示了真实的正负类数据;©显示了用于模型训练的未标注数据和有标注偏差的正类数据;(b)和(d)表示真实的 和LBE-LF估计的 ;(e)-(j)显示了uPU、nnPU、LDCE、PUSB、PWE和LBE-LF生成的分类结果。每种方法的分类准确率都显示在相应的子图上方。
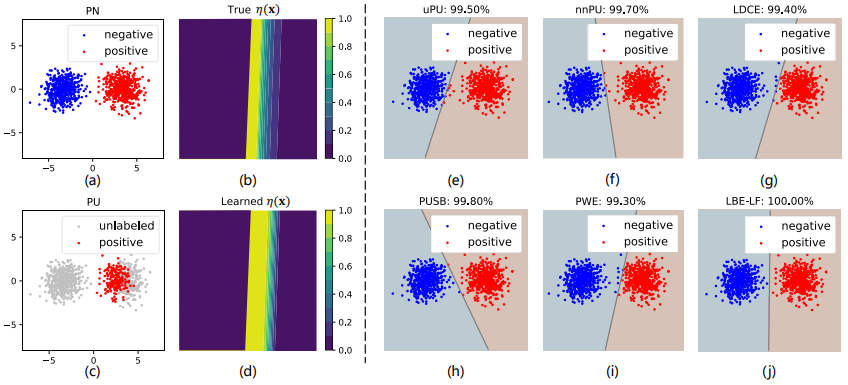 图3 策略2下各种方法在合成数据集上的表现。(a)显示了真实的正负类数据;©显示了用于模型训练的未标注数据和有标注偏差的正类数据;(b)和(d)表示真实的 和LBE-LF估计的 ;(e)-(j)显示了uPU、nnPU、LDCE、PUSB、PWE和LBE-LF生成的分类结果。每种方法的分类准确率都显示在相应的子图上方。
图3 策略2下各种方法在合成数据集上的表现。(a)显示了真实的正负类数据;©显示了用于模型训练的未标注数据和有标注偏差的正类数据;(b)和(d)表示真实的 和LBE-LF估计的 ;(e)-(j)显示了uPU、nnPU、LDCE、PUSB、PWE和LBE-LF生成的分类结果。每种方法的分类准确率都显示在相应的子图上方。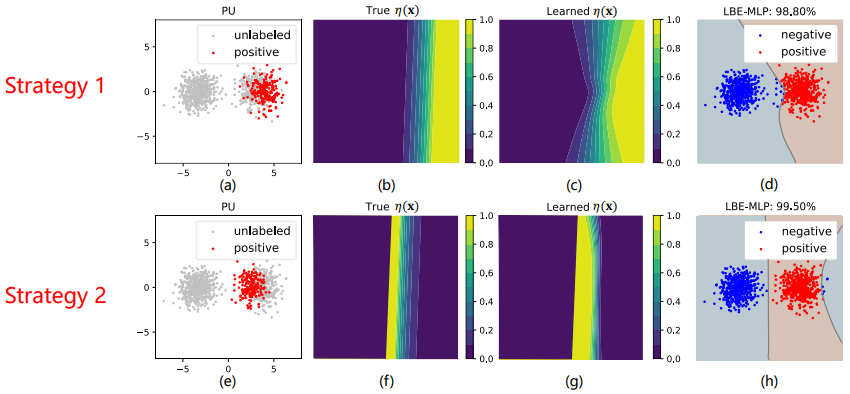 图4 LBE-MLP在策略1和策略2下的合成数据集上的表现。上图是策略1,其中(a)-(d)显示了用于模型训练的未标注数据和有标注偏差的正类数据、真实的 、通过LBE-MLP估计的 和LBE-MLP的分类结果。下图是策略2,其中(e)-(h)与(a)-(d)含义相同。
图4 LBE-MLP在策略1和策略2下的合成数据集上的表现。上图是策略1,其中(a)-(d)显示了用于模型训练的未标注数据和有标注偏差的正类数据、真实的 、通过LBE-MLP估计的 和LBE-MLP的分类结果。下图是策略2,其中(e)-(h)与(a)-(d)含义相同。
四、总结
现有的PU学习方法大多是实例无关的学习方法,这类方法往往和实际情况不相符。为了解决这一问题,本文提出了一种新的实例相关PU学习方法——“LBE”,它估计了正类数据的标注偏差并训练分类器。通过该方法模型的构建过程和对实验结果的分析,可以得到LBE的优势包括四个方面:
1. 一般性:该模型框架的一般性包括两个方面,一是LBE可以广泛地适应当下的主流分类器,如本文提出的LF和MLP;另一方面,只要改变用户定义的 ,LBE就可以灵活地描述各种标注偏差。
2. 最优性:LBE可以利用具有明确目标函数的Logistic回归来实现,并且可以从理论上证明其解的存在性和局部唯一性。
3. 泛化性:可以从理论上证明,对于LBE模型如果正类数据和未标注数据的数量足够大,期望风险将收敛于经验风险,即该模型在未知数据上具有良好的泛化性。
4. 实用性:LBE模型与许多现有的PU分类器不同,其不需要预先估计先验概率 ,并且该先验概率实际上不容易获得。此外,LBE模型不包含任何超参数。因此,它可以在各种实际场景下轻松实现。
[1] C.Gong, Q. Wang, T. Liu, B. Han, J. You, J. Yang, and D. Tao, “Instance-Dependent Positive and Unlabeled Learning with Labeling Bias Estimation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021.
[2] M. Du Plessis, G. Niu, and M. Sugiyama, “Convex formulation for learning from positive and unlabeled data,” in International Conference on Machine Learning, 2015, pp. 1386–1394.
[3] R. Kiryo, G. Niu, M. C. du Plessis, and M. Sugiyama, “Positive-unlabeled learning with non-negative risk estimator,” in Advances in Neural Information Processing Systems, 2017, pp. 1674–1684.
[4] H. Shi, S. Pan, J. Yang, and C. Gong, “Positive and unlabeled learning via loss decomposition and centroid estimation.” in International Joint Conferences on Artificial Intelligence, 2018, pp. 2689–2695.
[5] C. Gong, H. Shi, T. Liu, C. Zhang, J. Yang, and D. Tao, “Loss decomposition and centroid estimation for positive and unlabeled learning,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019.
[6] C. Gong, T. Liu, J. Yang, and D. Tao, “Large-margin label-calibrated support vector machines for positive and unlabeled learning,” IEEE Transactions on Neural Networks and Learning Systems, pp. 1–13, 2019.
[7] C. Zhang, D. Ren, T. Liu, J. Yang, and C. Gong, “Positive and unlabeled learning with label disambiguation,” in International Joint Conference on Artificial Intelligence, 2019, pp. 4250–4256.
[8] C. Gong, H. Shi, J. Yang, J. Yang, and J. Yang, “Multi-manifold positive and unlabeled learning for visual analysis,” IEEE Transactions on Circuits and Systems for Video Technology, 2019.
[9] M. Kato, T. Teshima, and J. Honda, “Learning from positive and unlabeled data with a selection bias,” in International Conference on Learning Representation, 2019, pp. 1–12.
[10] J. Bekker, P. Robberecht, and J. Davis, “Beyond the selected completely at random assumption for learning from positive and unlabeled data,” in ECML-PKDD, 2019, pp. 1–16.
本文来自:公众号【京东探索研究院】
作者:荆子辉
Illustrastion by Semenin Egor from Icons8

扫码观看!
本周上新!

“AI技术流”原创投稿计划
TechBeat是由将门创投建立的AI学习社区(www.techbeat.net)。社区上线330+期talk视频,900+篇技术干货文章,方向覆盖CV/NLP/ML/Robotis等;每月定期举办顶会及其他线上交流活动,不定期举办技术人线下聚会交流活动。我们正在努力成为AI人才喜爱的高质量、知识型交流平台,希望为AI人才打造更专业的服务和体验,加速并陪伴其成长。
投稿内容
// 最新技术解读/系统性知识分享 //
// 前沿资讯解说/心得经历讲述 //
投稿须知
稿件需要为原创文章,并标明作者信息。
我们会选择部分在深度技术解析及科研心得方向,
对用户启发更大的文章,做原创性内容奖励。
投稿方式
发送邮件到
chenhongyuan@thejiangmen.com
或添加工作人员微信(chemn493)投稿,沟通投稿详情;还可以关注“将门创投”公众号,后台回复“投稿”二字,获得投稿说明。

>> 投稿请添加工作人员微信!
关于我“门”
▼

点击右上角,把文章分享到朋友圈
点击“阅读原文”按钮,查看社区原文
⤵一键送你进入TechBeat快乐星球