深度学习模型中的信任危机及校正方法

将门创投 2022-01-12 08:22

深度学习在计算机视觉、自然语言处理、数据挖掘等诸多研究领域中的潜力被广泛认可，在目标检测、语音识别、医疗检测、金融欺诈检测等多种实际任务中也性能卓越。然而在追求卓越性能的过程之中，越来越多的研究者开始注意到性能背后的可信性问题（Trustworthiness）。尤其是当深度模型步入到实际应用中的风险敏感场景中时，深度模型结果的可信性更加成为一个迫切的需求。以自动驾驶系统设计为例，研究者期望模型的所有预测均是可信的，因为错误的预测可能会导致车祸的发生，带来灾难性后果。然而事实上，模型不可能做出100%正确的预测。

题目：
深度学习模型中的信任危机及校正方法
作者：
北邮 GAMMA Lab 硕士生刘洪瑞，副教授王啸

一、前言

如何定义深度模型的可信性呢？

可信性的范畴其实见仁见智，其中一种思想是认为深度模型的置信度应该是符合“道理”的。简单来讲，也即深度模型对其预测的结果应该“知道它知道什么，同时也要知道它不知道什么”。更术语一点讲，可以认为是深度模型对其预测正确的结果，应该给予较高的置信度，对于预测错误的结果，则应该有较低的置信度。在这种情况下，自动驾驶系统就可以仅采纳高置信（如0.99）的预测，因为这代表了高准确率的预测（只有1%的概率出错），而拒绝低置信的预测，这也就意味着模型的可信性得到了实现。在本文中，我们用置信度的校正性来衡量置信度是否符合“道理”。

通常置信度可以定义为

，其中为样本的逻辑（Logit）向量，即多分类问题下模型层的输入，为算子。基于此，我们称当置信度可以准确反映其预测准确率时，即满足如下定义时，是被完美校正的（Perfectly Calibrated）：

即，对于任意样本与其真实标签，当模型对该样本预测的置信度时，该预测是正确预测的概率同样为。举例来讲，如果模型对某100个样本的预测均有0.8的置信度，且100个样本中同样有80%的样本被预测正确，我们就可以认为该置信度在0.8附近是被校正的。

那么，在众多深度学习方法中，模型的置信度是否是被完美校正的呢？

二、对置信度校正性的探究

对深度学习领域置信度校正性的探究源于卡耐基梅隆大学的Chuan Guo等人在ICML 2017的一篇论文《On Calibration of Modern Neural Networks》[1]，其分别分析了在计算机视觉和自然语言处理领域中，多个当时的最新模型（ResNet, DenseNet, LSTM）在不同数据集（CIFAR-10, CIFAR-100, ImageNet, 20 News）下置信度的校正性，并利用了可靠性直方图进行可视化，如下图所示：

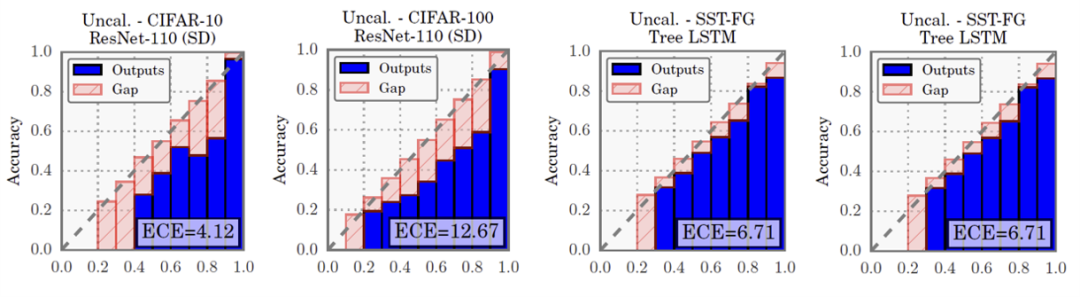
其中直方图的横坐标代表模型对预测的置信度，纵坐标代表预测的准确率。为了便于展示，作者将置信度区间[0,1]等间隔划分为了十个置信度子区间，并分别统计每一子区间中预测的平均准确率，实际结果如蓝色柱状图所示。显然，如果模型的置信度是被完美校正的，则柱状图顶端应该恰好符合对角线分布（如红色柱状图所示）。我们可以看到，实际上，蓝色柱状图整体分布于对角线的下方。因此，作者指出目前多数深度学习模型的置信度并没有被完美校正，且整体呈现出过于自信的（Over-Confident）倾向，即预测的平均置信度高于预测的平均准确率。

自此，众多研究者开始致力于寻找到深度学习模型置信度校正能力差的理论解释。[2] 指出置信度校正能力差源于深度神经网络的过参数化现象，即网络模型过于庞大以致于其可以记住整个训练集，因而能最大化几乎所有样本的置信度。但是 [3] 理论证明了最简单的逻辑回归模型也是过于自信的，因此模型的校正能力和网络参数量并没有直接的关系，并给出了在经验风险最小化（Empirical Risk Minimization，ERM）问题中，当损失函数满足一定限制时，模型过于自信和不自信的充分条件。但事实上，正则化项对置信度的校正性有相当重要的影响[1, 4, 5]，而在结构风险最小化（Structural Risk Minimization，SRM）问题中对置信度校正性的解释仍有待探索。

尽管研究者早已对传统深度学习模型的置信度校正进行了广泛而又深入的研究，但是还鲜有人关注到图神经网络领域，我们在[9]中首先探索了半监督分类问题下图神经网络的置信度校正问题。具体来说，我们研究了多个有代表性的图神经网络模型在Cora、Citeseer、Pubmed和CoraFull等四个数据集中置信度的校正性，部分实验结果如下图所示：

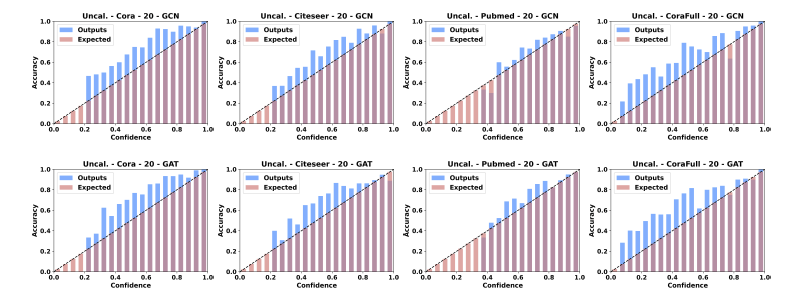
我们却观察到，在大部分情况下，可靠性直方图中的蓝色柱高于红色柱，即分类准确率高于其置信度，这说明图神经网络模型的置信度也没有被很好地校正，模型对其预测是不自信的（Under-Confident）。这种现象与刚刚阐述过的计算机视觉和自然语言处理领域中的结论是不同的。

三、如何校正深度学习模型的置信度

自从 Chuan Guo 等人提出深度神经网络模型的置信度存在校正能力差的问题后，近几年来已经涌现出了诸多置信度校正方法，极大地促进了该领域的发展。本文将主要介绍4种可以用来处理深度学习模型以及图神经网络模型的置信度校正方法。

3.1 Temperature Scaling

Temperature Scaling 是知识蒸馏中一种常用的软标签平滑方法，即利用一个温度系数对预测概率向量进行平滑或尖锐化，Chuan Guo 等人[1] 最早将其作为了置信度校正方法。具体来说，给定任意一个样本的逻辑向量，经过Temperature Scaling校正后的置信度为：

其中是一个可学习参数，一般通过优化验证集样本的交叉熵损失函数学习到。

当时，Temperature Scaling 会平滑的输出，进而减小预测的置信度，缓解模型过自信的问题；相反，当时，的输出将变得越来越尖锐，对预测的置信度会趋近于1，这将有助于缓解对预测的不自信问题。此外，由于是一个大于零的参数，因此经过Temperature Scaling变换之后，向量各维度之间的序并不会发生改变，因此模型的预测也不会发生改变，因此利用Temperature Scaling做置信度校正并不会影响到模型的分类性能。

3.2 Isotonic Regression

保序回归（Isotonic Regression，IR） [6] 是一种适用于二分类问题的非参数化的置信度校正方法，其旨在学习一个分段线性的保序函数对置信度进行校正：。保序回归常用的保序函数求解方法是PAV算法（Pair-Adjacent Violators Algorithm）[7]，主要思想是通过不断合并、调整违反单调性的局部区间，使得最终得到的区间满足单调性。此外，PAV算法也是scikit-learn中isotonic regression库的求解算法。

PAV算法描述如下所示：

即，对于一个无序数字序列，PAV会从该序列的首元素往后观察，一旦出现乱序现象停止该轮观察，从该乱序元素开始逐个吸收元素组成一个序列，直到该序列所有元素的平均值小于或等于下一个待吸收的元素。更详细的描述可以参见知乎文章 https://zhuanlan.zhihu.com/p/88623159。

3.3 Min-n-Match

Mix-n-Match [8] 一文对此前出现的诸多置信度校正方法进行了系统的分析，并提出了一个合理的置信度校正方法应该满足以下三个条件：

1. 不改变模型的分类性能

2. 数据有效性——不需要大量训练数据即可得到较好的置信度校正函数

3. 表达能力强——能够近似任意需要的置信度校正函数。

为此，该文组合了此前的诸多置信度校正方法，弃其糟粕，取其精华，提出了Mix-n-Match方法。

首先，对Temperature Scaling方法进行了改进，提出Ensemble Temperature Scaling (ETS)，以提升该方法的表达能力，即：

其中，是类别个数，是分类模型的输出，被称之为预测概率向量。

然后，对Isotonic Regression进行了改进，使其可以扩展到多分类问题。具体来说：

step1：对于所有参与到训练置信度校正函数的个样本的预测概率向量，将其所有个维度的值抽取出来，构成一个新的集合。同样，对这些样本的one-hot标签进行相同的操作，得到。对两个集合按照的大小进行排序

step2：利用PAV算法在与上学习一个保序函数：

step3：使是一个严格保序函数，即，其中是一个极小的常数。

最后，组合ETS和改进的IR，得到Mix-n-Match，如下所示：

3.4 CaGCN

CaGCN[9]是第一个对图神经网络中的置信度进行校正的方法，其设计考虑到了图数据结构中独特的拓扑结构信息，并详细分析了在对图神经网络中的置信度进行校正时考虑拓扑信息的必要性。

具体来说，考虑两个节点a, b，其中 a 节点处于高同配性的区域，即 a 节点与其邻居节点的特征和标签均相近，而 b 节点处于高异配性的区域。根据第2节提到的图神经网络的置信度校正性差的结论，我们可以假设节点a和b的置信度均没有被很好的校正，此外，为了便于分析，我们额外假设两节点的逻辑向量相近。

根据之前的研究结论，具有代表性的图神经网络模型如GCN、GAT等在高同配性的数据集中表现更好，因此我们可以认为节点 a 应该具有更高的置信度，而相应地，节点b的置信度应该比较低。然而，在不考虑到网络的拓扑结构的情况下，由于两节点的逻辑向量相近（如前面所述，一般是校正函数的输入），因此只能对 a 和 b 进行相同方向的校正，而无法同时使 a 的置信度变高并使 b 的置信度变低。所以，理论上讲，CV 和 NLP 中提出的置信度校正方法事实上并不适用于图数据结构。

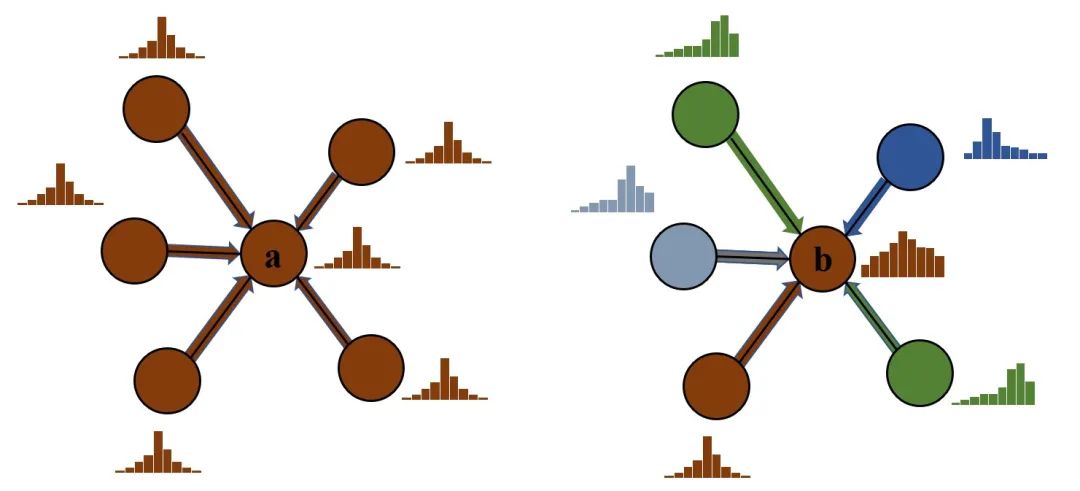
基于上述分析，[9]提出了考虑到网络拓扑结构的校正方法CaGCN。CaGCN的设计基于置信度分布的同配性假设，即相邻节点的置信度趋向于相同有利于置信度校正，我们通过实验验证了该假设。具体来说，我们对比了未进行置信度校正时和经过Temperature Scaling（TS）校正后置信度总变差的变化，其中置信度的总变差被用来衡量其同配性，总变差越小，说明相邻节点的置信度越相近，因此置信度分布的同配性越强；而Temperature Scaling 是公认的性能较好的置信度校正方法。实验结果如下表所示：

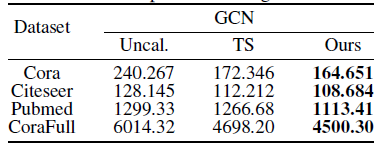
可以清楚地看到，经过TS进行置信度校正后，节点置信度的总变差有明显下降，这证明了我们之前的假设。考虑到GCN 天然可以平滑邻居节点特征，我们利用 GCN 模型作为我们基础的置信度校正函数，如下所示：

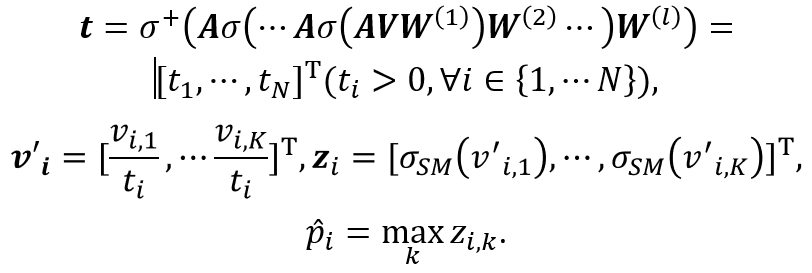
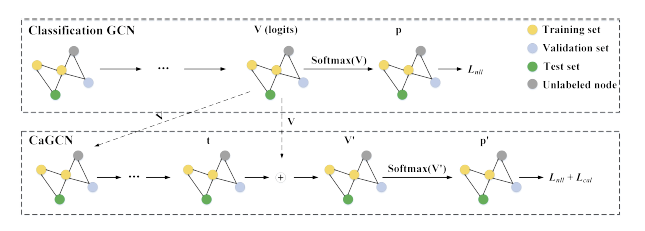
即以分类模型的输出作为输入，利用GCN为每一个节点学习到一个单独的温度系数，然后进行Temperature Scaling变换。可以看到，温度系数的计算考虑到了网络的拓扑结构，满足了我们的设计初衷。CaGCN的模型图如下所示：

更详细的介绍，可以参考论文：https://proceedings.neurips.cc/paper/2021/hash/c7a9f13a6c0940277d46706c7ca32601-Abstract.html

参考文献

[1] Guo C, Pleiss G, Sun Y, et al. On calibration of modern neural networks[C]//International Conference on Machine Learning. PMLR, 2017: 1321-1330.

[2] Mukhoti J, Kulharia V, Sanyal A, et al. Calibrating deep neural networks using focal loss[J]. arXiv preprint arXiv:2002.09437, 2020.

[3] Bai Y, Mei S, Wang H, et al. Don’t Just Blame Over-parametrization for Over-confidence: Theoretical Analysis of Calibration in Binary Classification[J]. arXiv preprint arXiv:2102.07856, 2021.

[4] Gal Y, Ghahramani Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning[C]//international conference on machine learning. PMLR, 2016: 1050-1059.

[5] Thulasidasan S, Chennupati G, Bilmes J, et al. Improved calibration and predictive uncertainty for deep neural networks[J]. arXiv preprint arXiv:1905.11001, 2019.

[6] Zadrozny, Bianca and Elkan, Charles. Obtaining calibrated probability estimates from decision trees and naive bayesian classifiers. In ICML, pp. 609–616, 2001.

[7] Ayer, M., Brunk, H. D., Ewing, G. M., Reid, W. T., and Silverman, E. An empirical distribution function for sampling with incomplete information. The Annals of Mathematical Statistics, pp. 641–647, 1955.

[8] Zhang J, Kailkhura B, Han T Y J. Mix-n-match: Ensemble and compositional methods for uncertainty calibration in deep learning[C]//International Conference on Machine Learning. PMLR, 2020: 11117-11128.

[9] Wang X, Liu H, Shi C, et al. Be Confident! Towards Trustworthy Graph Neural Networks via Confidence Calibration[J]. Advances in Neural Information Processing Systems, 2021, 34.