你看!这电路我玩得溜吗?
以下文章来源于涛歌依旧 ,作者点击关注👉👉
涛哥CSDN排名第一,曾就职于华为和鹅厂。公众号内容:编程之路、面试刷题、职场进阶、杂文荟萃。
电路是我的本行,电路基础、模拟电路、数字电路、高频电路,我还是比较熟悉的。而计算机编程嘛,是为了混口饭吃,半路出家自学。接下来,我会用电路来做计算器、计算机,并介绍编程。
计算机的功能,都是通过计算来完成的,而计算是怎样完成的呢?答案是:电路。我们探讨了编码的本质和计算机的工作原理,讲了二进制的加法,今天我们动手做一个计算器,实现加法功能。
读初二时,在陈老师的物理课堂上,第一次听到了“大到太阳系、银河系,小到分子、原子、电子”,当时印象非常深刻。从那一刻起,我知道了电子是很小很小很小的东西,肉眼是不可能看到的。
我们每天吃着分子、原子和电子,喝着分子、原子和电子,拉着分子、原子和电子。电子在现代计算机中很重要,所以才叫电子计算机。今天不讲分子、原子和电子,而是用电路来做计算器。
一. 欧姆定律简介
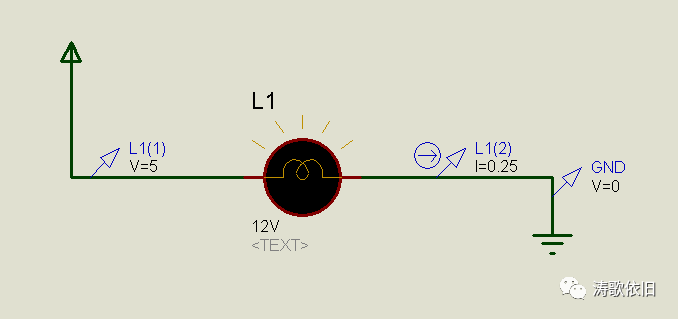
我们用proteus来进行电路仿真。福特、安培、欧姆附体,灯泡亮了。电源电压为5v, 灯泡电阻为20欧,电流为0.25A, 这正是欧姆定律要揭示的内容:
二. 二极管的验证
读初三时,在物理课上,听说过二极管,知道了二极管具有单向导电性。很显然,单向导电性决定了下图中的灯泡L1亮,而灯泡L2不亮,挺有意思的吧:
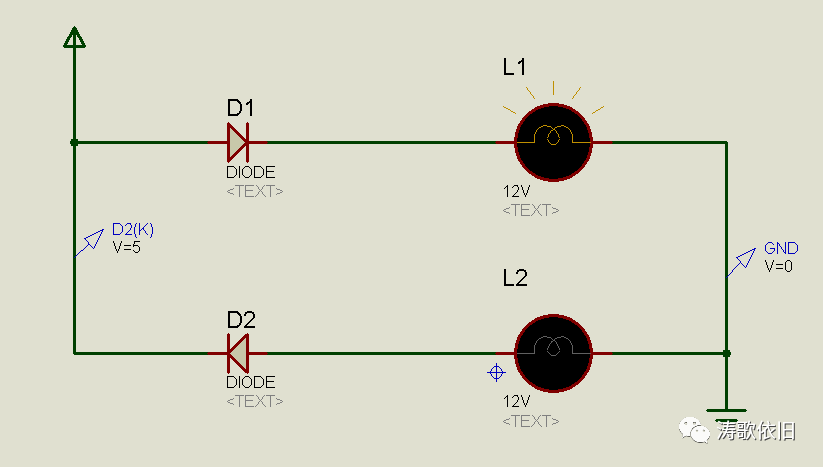
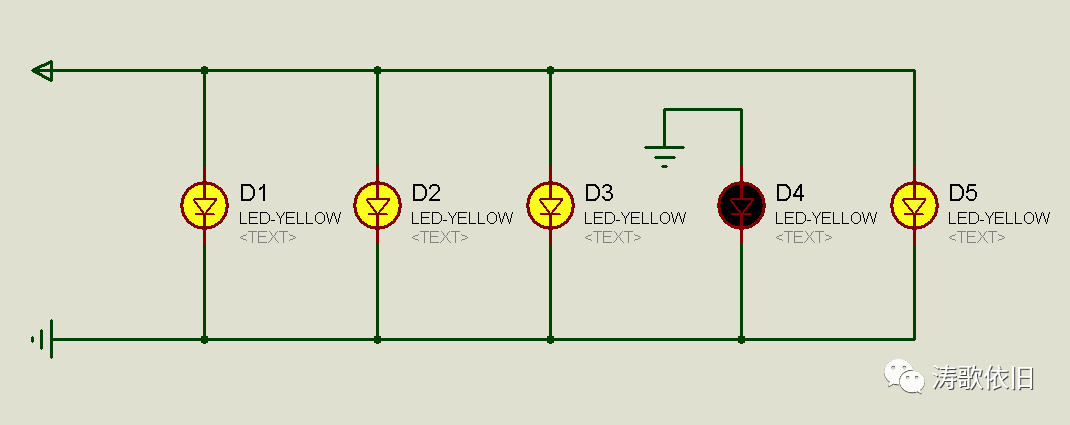
另外,二极管还有一个特性:二极管两端的电压差相对稳定。我们proteus仿真中用到的单项二极管,两端的电压差基本在0.7v到0.8v左右,验证如图:
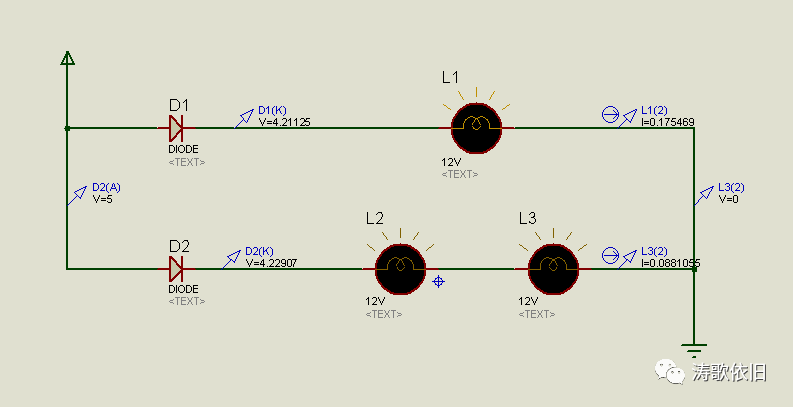
三. 与门电路简介
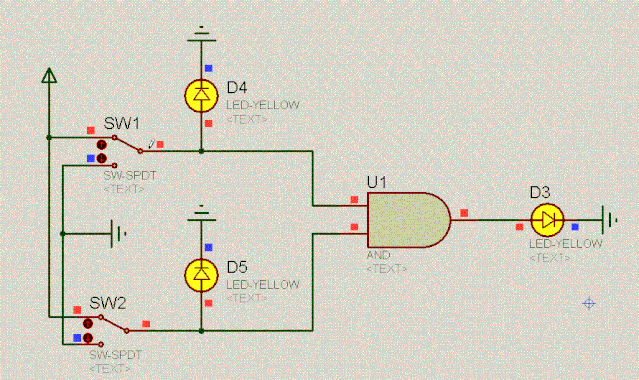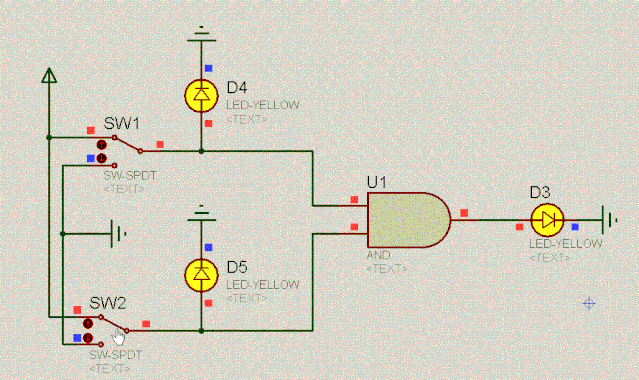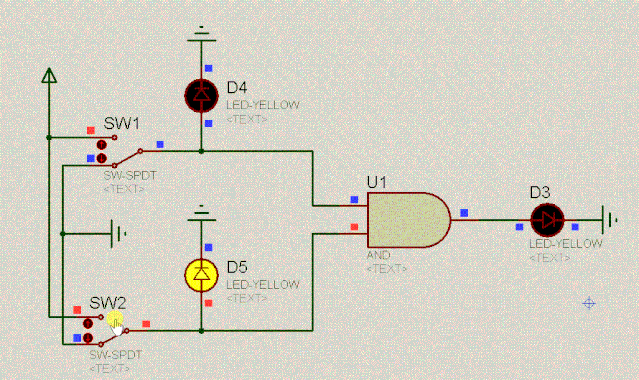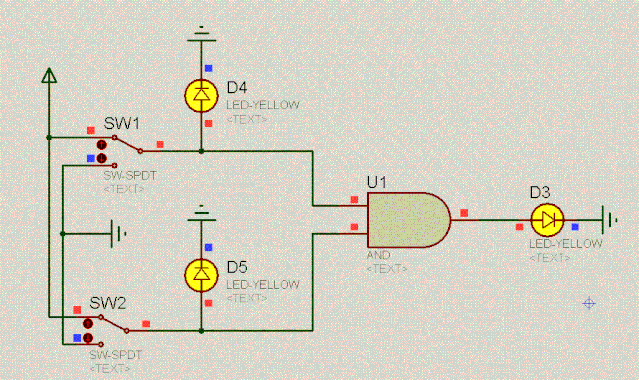
有了对二极管的基本认识,我们一起来看如下有趣的电路。根据二极管的单向导电性和两端相对恒定的电压差,不难分析出电路的特点。动图如下:
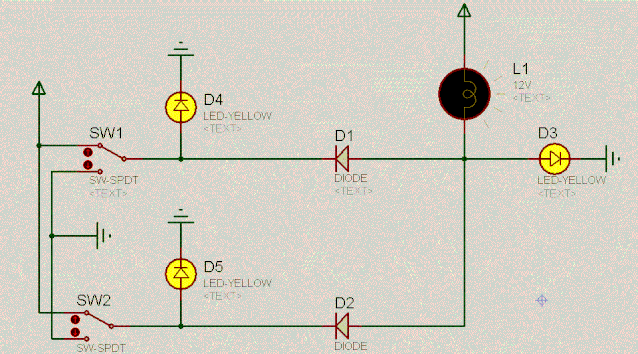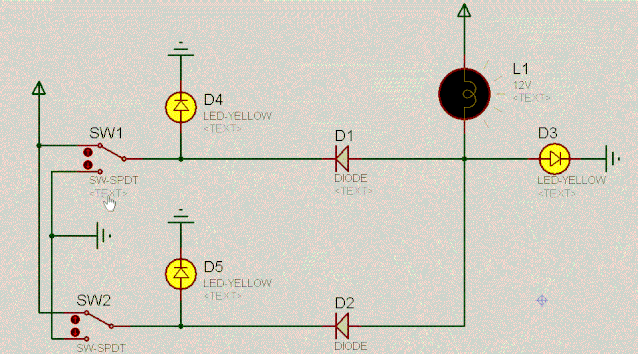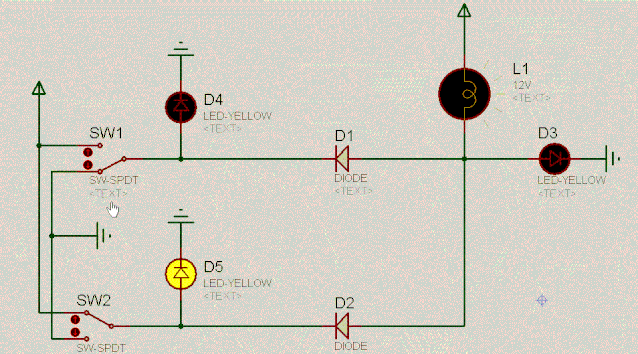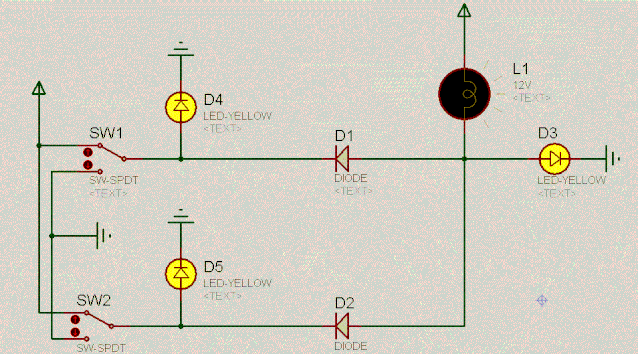
D4 | 操作 | D5 | D3 |
0 | 与 | 0 | 0 |
0 | 与 | 1 | 0 |
1 | 与 | 0 | 0 |
1 | 与 | 1 | 1 |
这不就是二进制的乘法吗?我们把上述这个电路叫作与门电路,其逻辑是:爸妈双方都同意你恋爱,你才能恋爱。
四. 或门电路简介
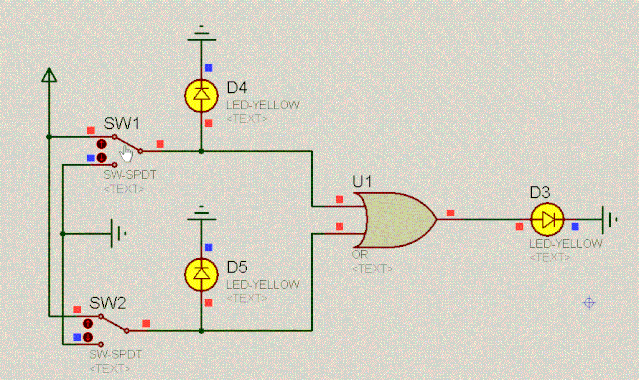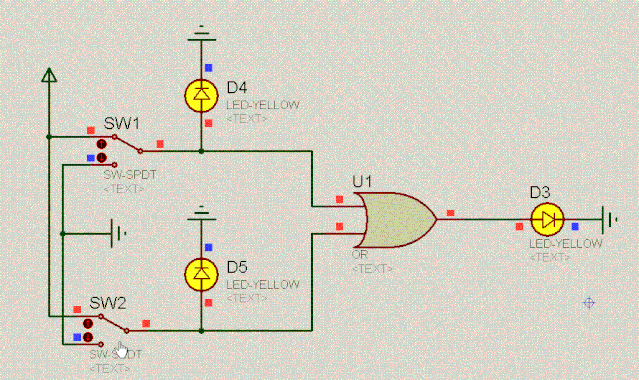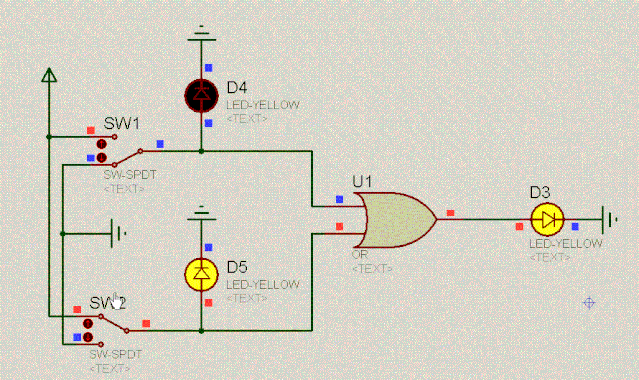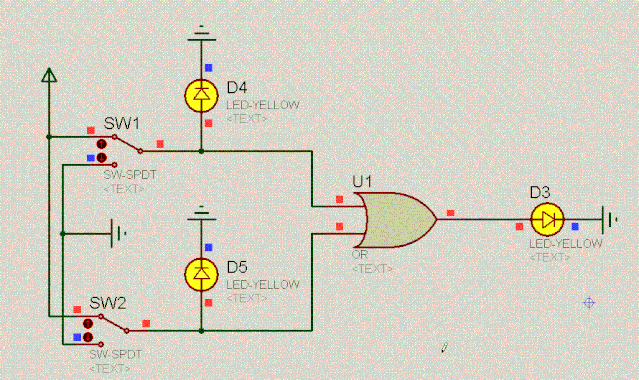
继续来看另外一个有趣的电路。根据二极管的单向导电性和两端相对恒定的电压差,容易分析出电路的特点。如下:
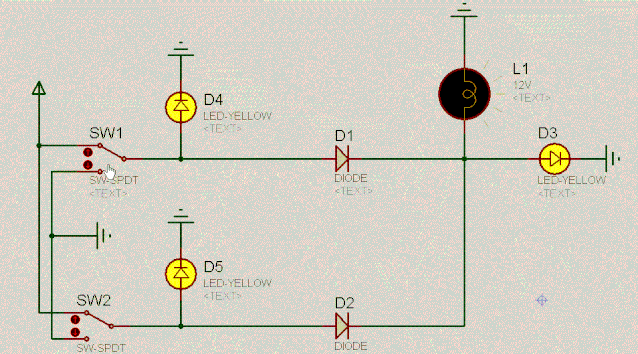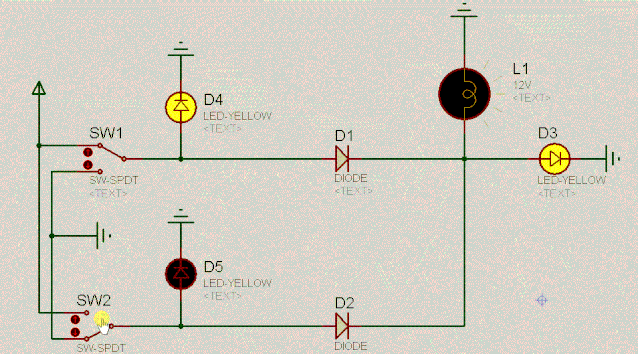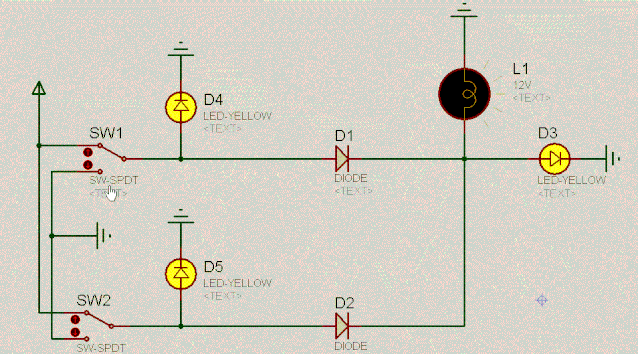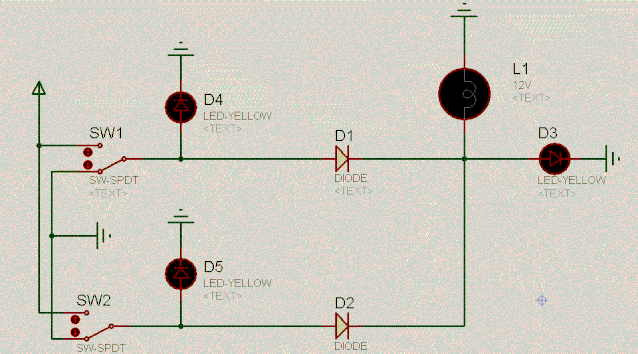
D4 | 操作 | D5 | D3 |
0 | 或 | 0 | 0 |
0 | 或 | 1 | 1 |
1 | 或 | 0 | 1 |
1 | 或 | 1 | 1 |
我们把上述这个电路叫作或门电路。其逻辑是:爸妈只要有一方同意你恋爱,你就可以恋爱。
五. 非门电路简介
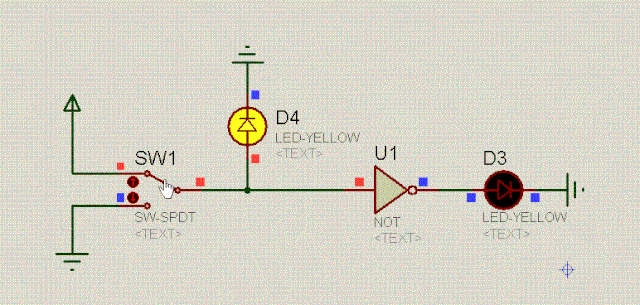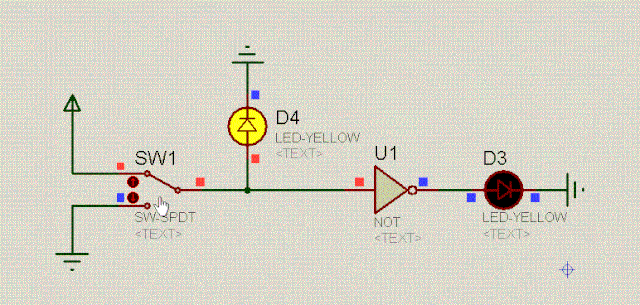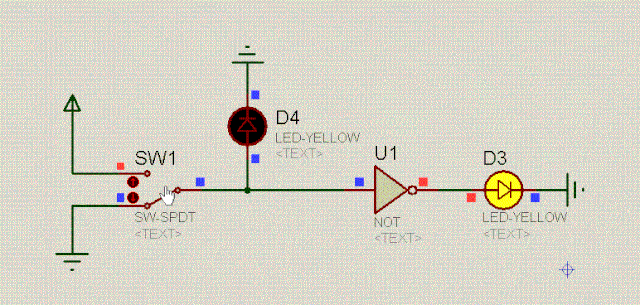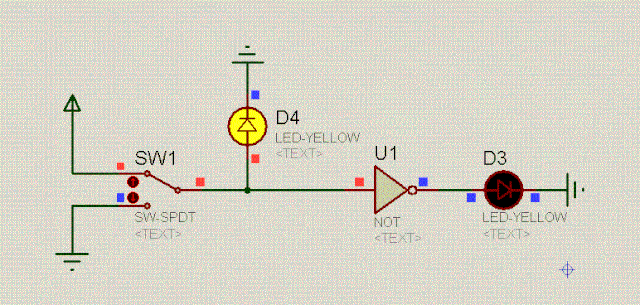
还有一个重要的电路,特性是,当输入是高电平时,输出是低电平,而当输入是低电平时, 输出是高电平,简直就是跷跷板。即:
输入 | 操作 | 输出 |
0 | 非 | 1 |
1 | 非 | 0 |
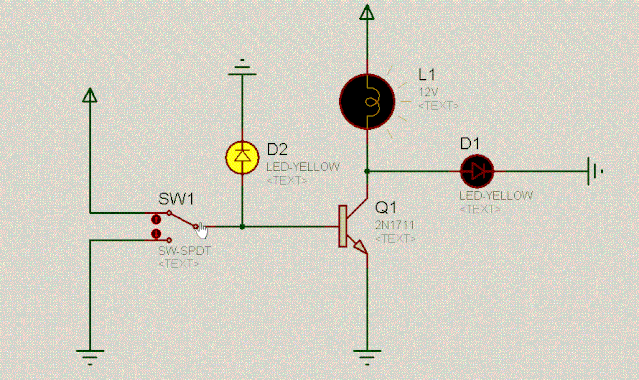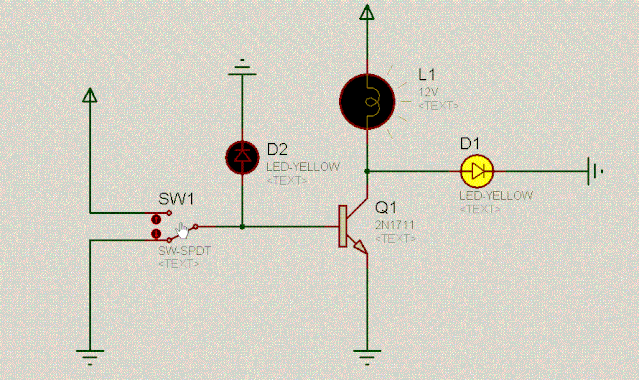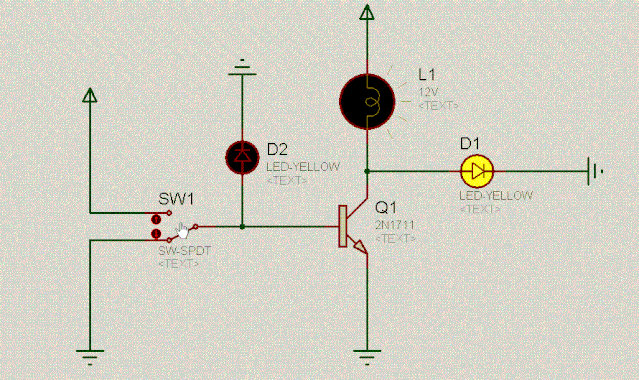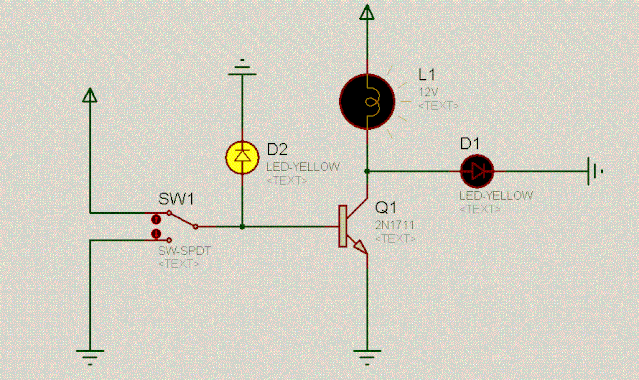
开关SW1相当于一个水闸开关,控制着三极管Q1,当SW1接高电平时,水闸打开,三极管通畅无阻,此时D1左边就好像是接地一样,显然,D1是不会亮的。
当开关SW1接低电平时(0v),三极管Q1堵塞住了,此时可以认为三极管断开了,直接从上图中摘掉三极管,于是乎,D1和灯泡L1形成了串联,自然D1就会亮。
可以看到,在非门电路中,D1和D2的值是相反的,其逻辑是:东方不亮西方亮,西方不亮东方亮。
上面的与门、或门、非门,太繁琐了,都是什么玩意儿!我们需要屏蔽这些底层细节和复杂性,怎么办?解决办法:抽象。抽象是计算机中重要的思想。
六. 与或非的抽象
直接来看抽象后的与门,即下图中的U1器件(U1下面那个灰色的AND, 就是与的意思),是不是简化了很多?这就是抽象的威力:
与门、或门和非门是三种最基本的电路逻辑器件,通过不断地组合、集成和抽象,可以形成功能更强大的器件。可以近似地认为,集成电路和芯片,就是功能不断组合、集成而来的,抽象度非常高。
七. 异或电路简介
我们来看如下电路图,它由基本的与门、或门和非门组成(先不要管为什么这样设计电路):
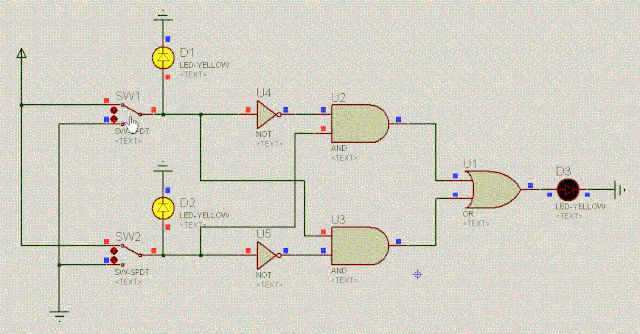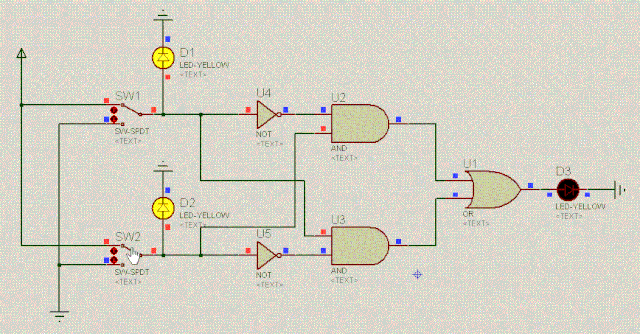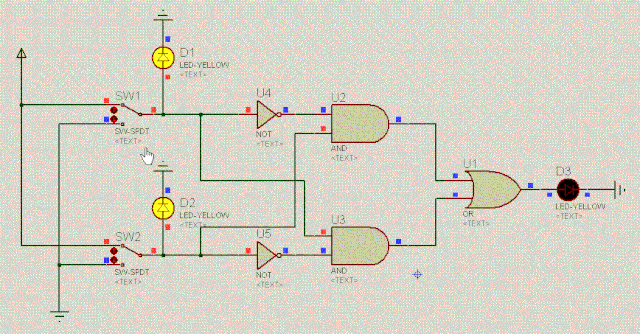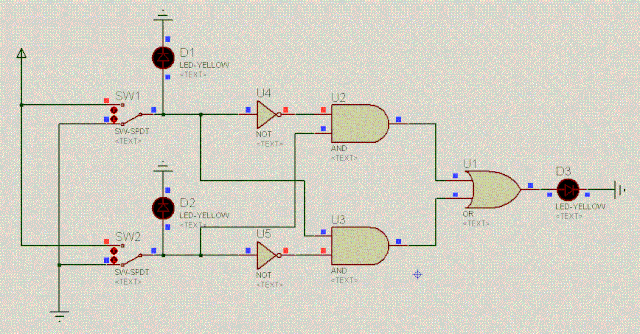
D1 | 操作 | D2 | D3 |
0 | 异或 | 0 | 0 |
0 | 异或 | 1 | 1 |
1 | 异或 | 0 | 1 |
1 | 异或 | 1 | 0 |
八. 半加器的电路
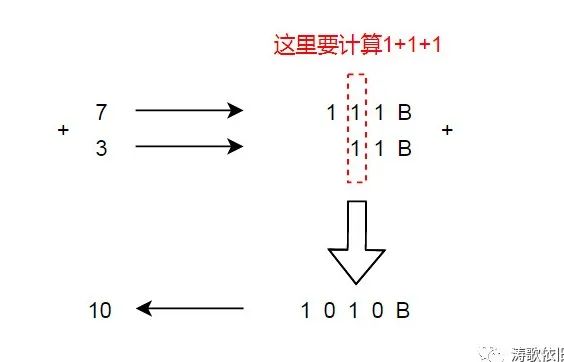
异或逻辑和二进制的加法,挺像哦!但是,貌似少了进位,我们期待的二进制加法逻辑是:
加数 | 操作 | 被加数 | 出进位 | 加法结果 |
0 | 加 | 0 | 0 | 0 |
0 | 加 | 1 | 0 | 1 |
1 | 加 | 0 | 0 | 1 |
1 | 加 | 1 | 1 | 0 |
现在终于明白了,不考虑进位时,二进制加法其实就是异或门逻辑。考虑进位时,进位的这一位其实就是与门逻辑。来看下电路,用D4表示进位,D3表示结果位:
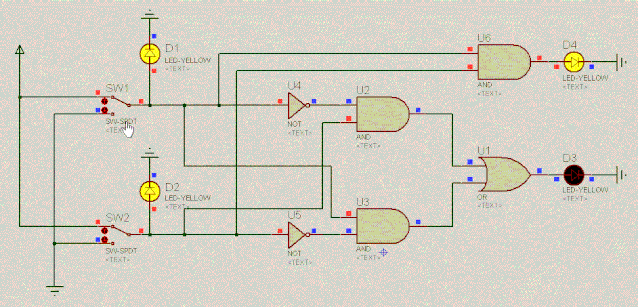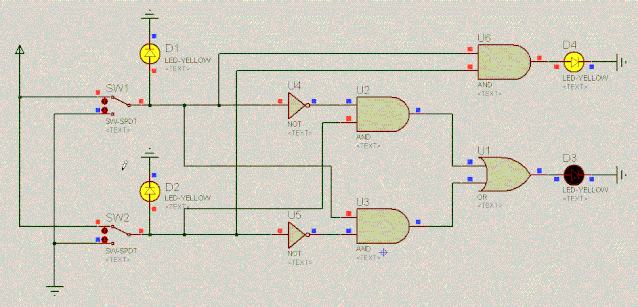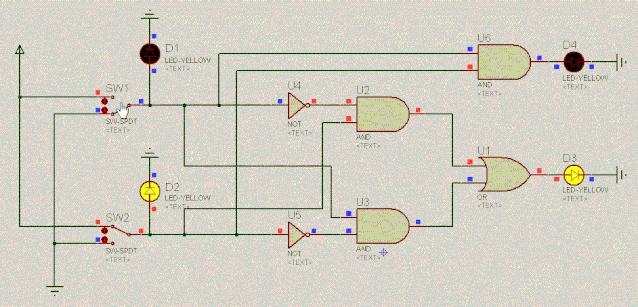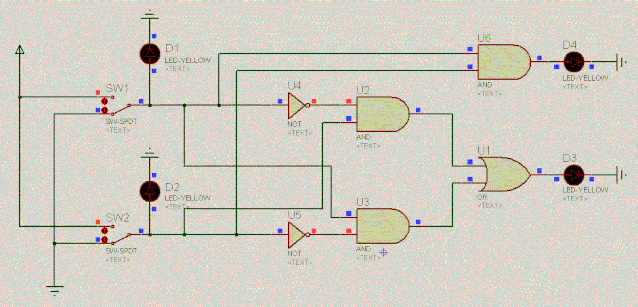
D1 | 操作 | D2 | 出进位D4 | D3 |
0 | 加 | 0 | 0 | 0 |
0 | 加 | 1 | 0 | 1 |
1 | 加 | 0 | 0 | 1 |
1 | 加 | 1 | 1 | 0 |
九. 全加器的电路
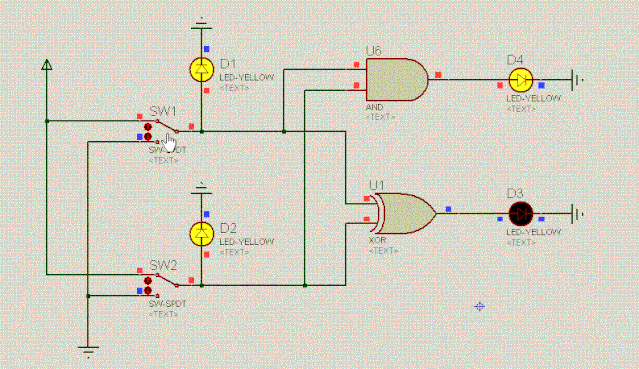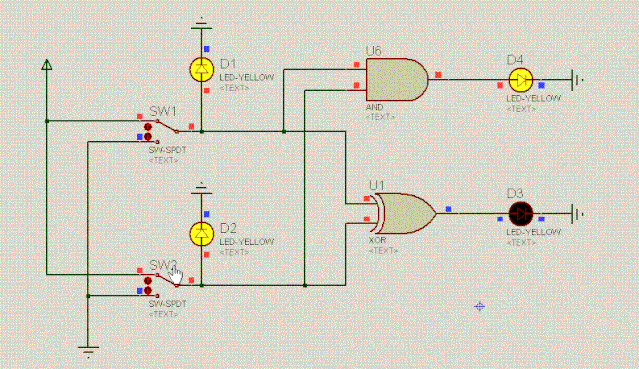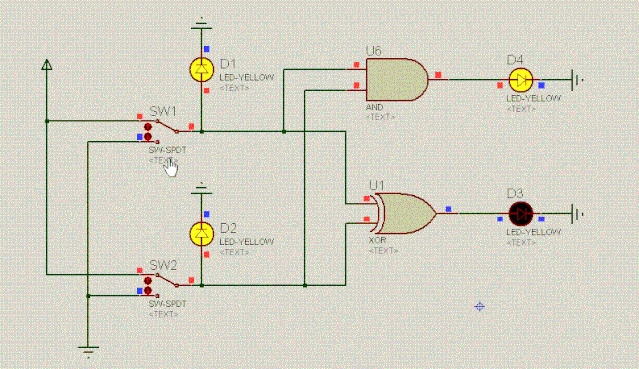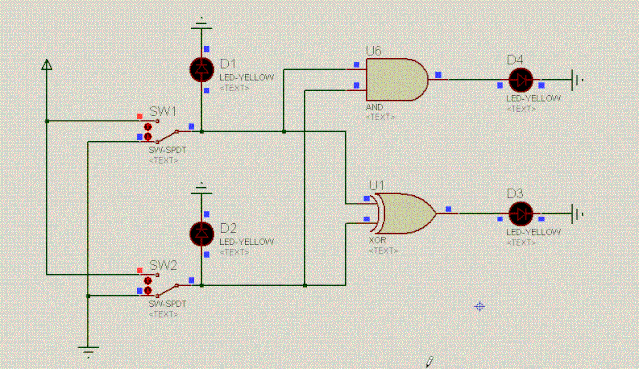
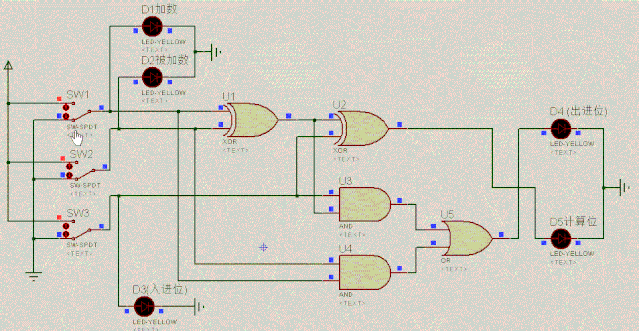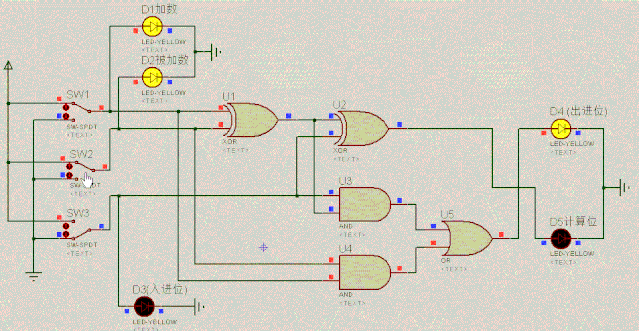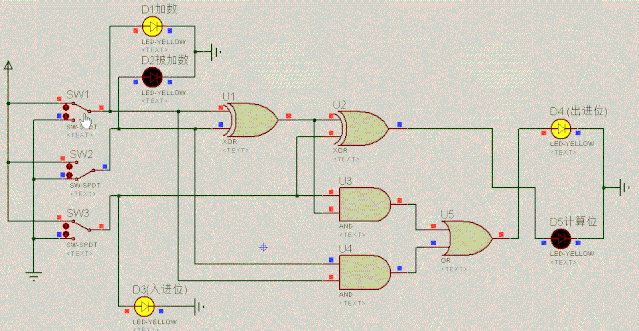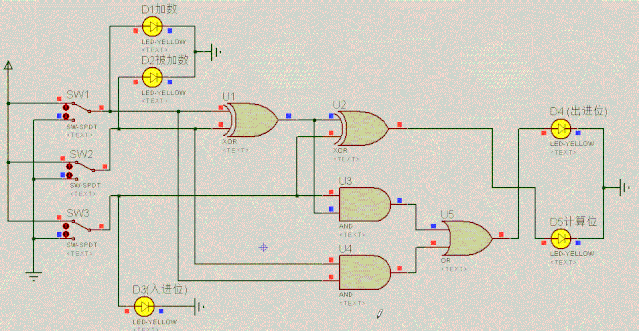
这就是二进制全加器,它能算出三个二进制位的和,全加器的逻辑功能如下:
加数D1 | 被加数D2 | 入进位D3 | 出进位D4 | 结果位D5 |
0 | 0 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 1 |
1 | 0 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 1 | 1 | 0 |
1 | 1 | 1 | 1 | 1 |
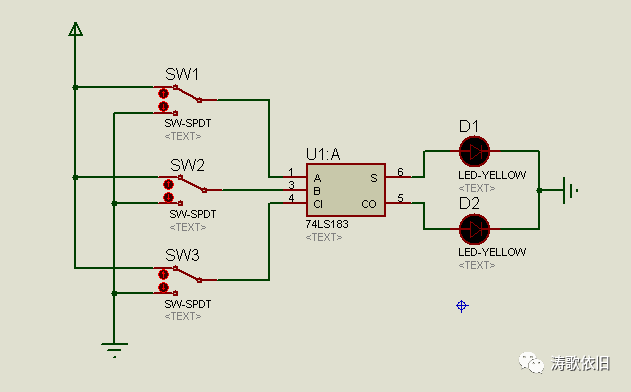
十. 2位全加器电路
上面的二进制全加器,是1位二进制全加器,只能在1个二进制位上进行操作,最大能计算1+1=2,如果我们把两个1位二进制全加器级联起来,就形成了一个2位二进制全加器,最大能计算3+3=6.
在介绍2位二进制全加器之前,我们先来简要了解一下数码管及其显示。在很多公共场合,我们都可以看见数码管的身影。刚从手机中找到了两年前的一张照片,记得当时是在地铁拍摄的,如下:

数码管中有很多条形灯管,通过控制条形灯管的亮与熄,可以显示不同的数字。数码管的形式有很多,上图数码管显示数字的范围是0-9.
本文介绍的数码管的显示范围是0-F, 也即十六进制的16个数字:0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 各进制对应关系如下所示:
十进制 | 二进制(B) | 十六进制(H) |
0 | 0 | 0 |
1 | 1 | 1 |
2 | 10 | 2 |
4-1 | 11 | 3 |
4 | 100 | 4 |
5 | 101 | 5 |
6 | 110 | 6 |
8-1 | 111 | 7 |
8 | 1000 | 8 |
9 | 1001 | 9 |
10 | 1010 | A |
11 | 1011 | B |
12 | 1100 | C |
13 | 1101 | D |
14 | 1110 | E |
16-1 | 1111 | F |
16 | 10000 | 10 |
17 | 10001 | 11 |
18 | 10010 | 12 |
19 | 10011 | 13 |
32-1 | 11111 | 1F |
64-1 | 111111 | 3F |
128-1 | 1111111 | 7F |
256-1 | 11111111 | FF |
512-1 | 111111111 | 1FF |
1024-1 | 1111111111 | 3FF |
对于熟悉二进制的程序员来说,1024才是整数,所以,10月24日被称为程序员节。来看下十六进制数码管的显示,0到9大家都认识,A-F长得有点丑,但足够表示数:
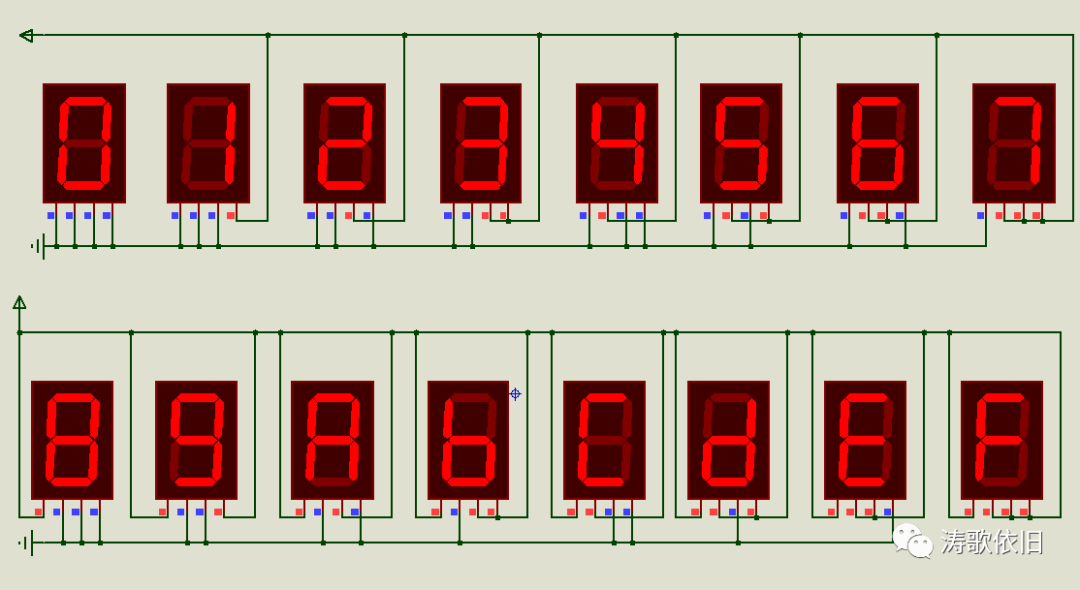
我们常在二进制数字后面加一个B, 用于区分十进制。同理,在十六进制数字后面,我们约定俗成地加一个H, 以便和十进制进行区分。
我们继续来制作2位二进制全加器。把两个1位二进制全加器级联以后,得到如下动图中的电路,可以看到,实现了两个数字的加法。
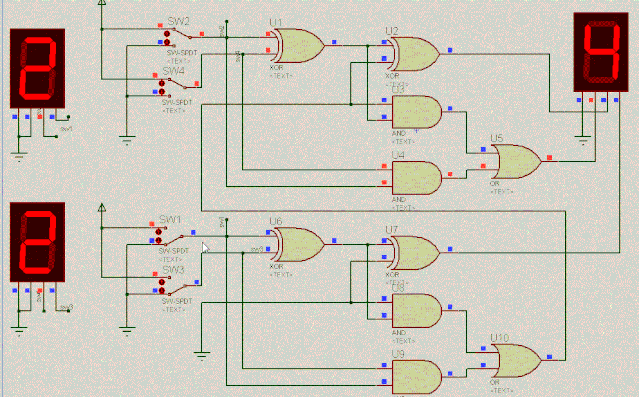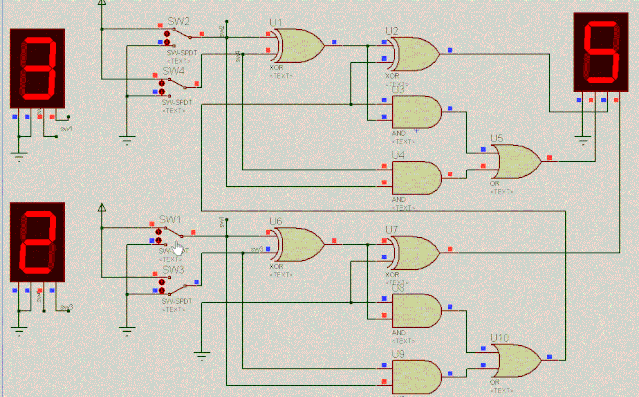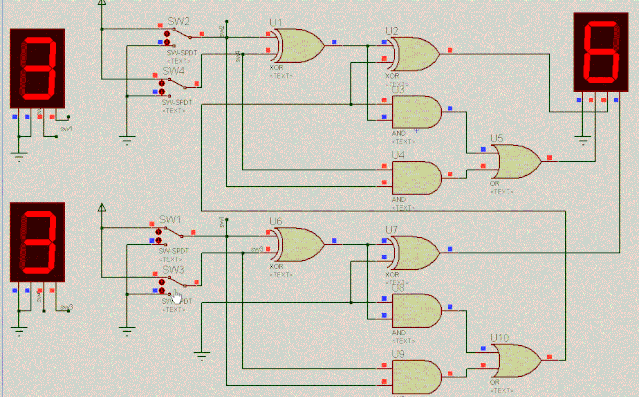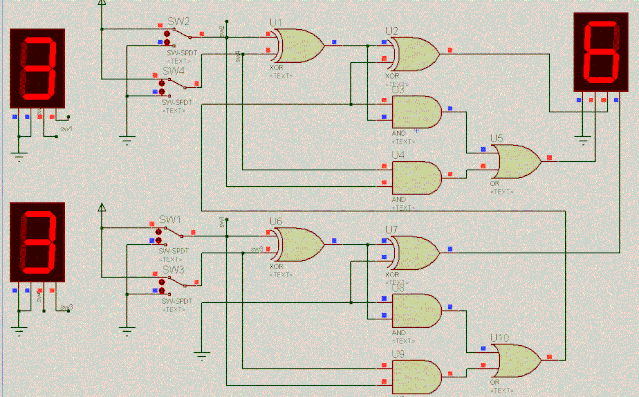
SW2 | SW1 | SW4 | SW3 | 完成计算 |
1 | 0 | 1 | 0 | 2+2=4 |
1 | 1 | 1 | 0 | 3+2=5 |
1 | 1 | 1 | 1 | 3+3=6 |
电路图越来越复杂了,得抽象一下了,直接使用封装好了的2位二进制全加器,如下面动图所示:
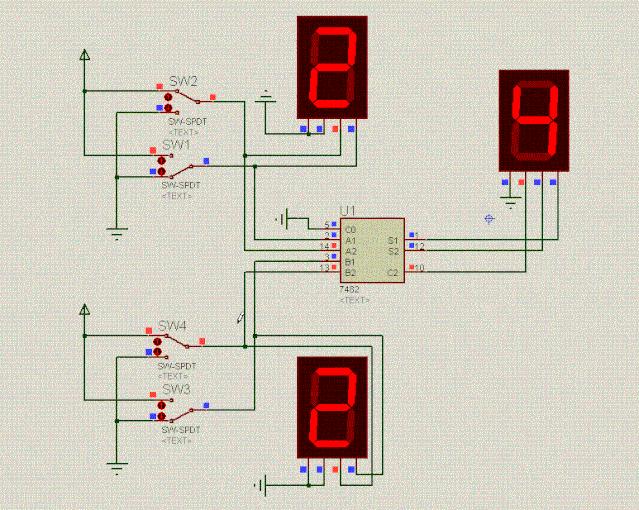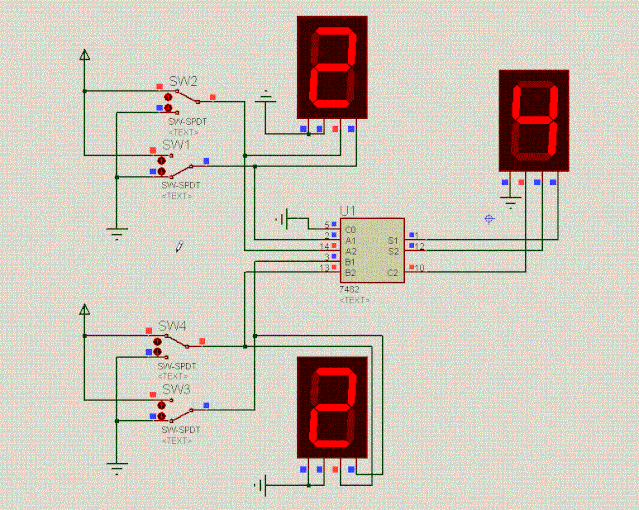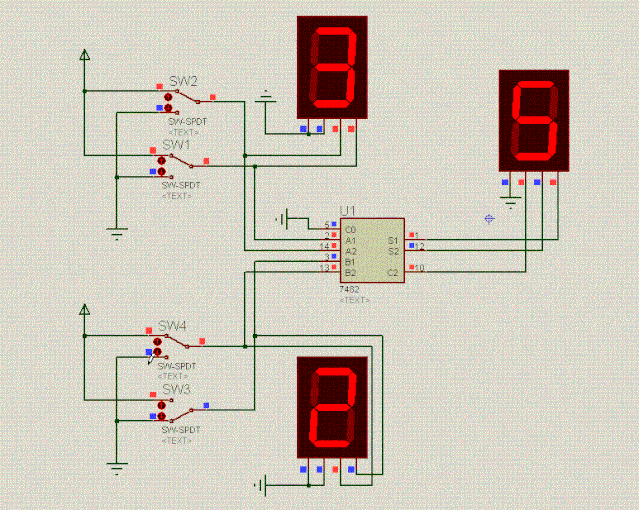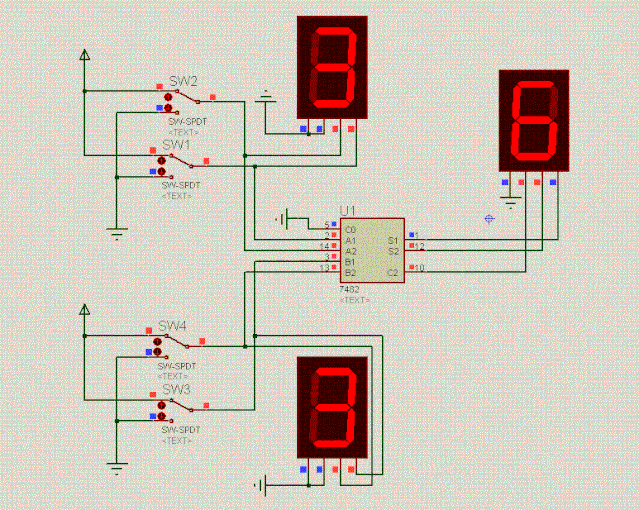
通过抽象,可以看到,电路图简单多了。抽象后的电路也完成了下表的加法计算,挺有意思的:
SW2(A2) | SW1(A1) | SW4(B2) | SW3(B1) | 完成计算 |
1 | 0 | 1 | 0 | 2+2=4 |
1 | 1 | 1 | 0 | 3+2=5 |
1 | 1 | 1 | 1 | 3+3=6 |
十一. 4位全加器电路
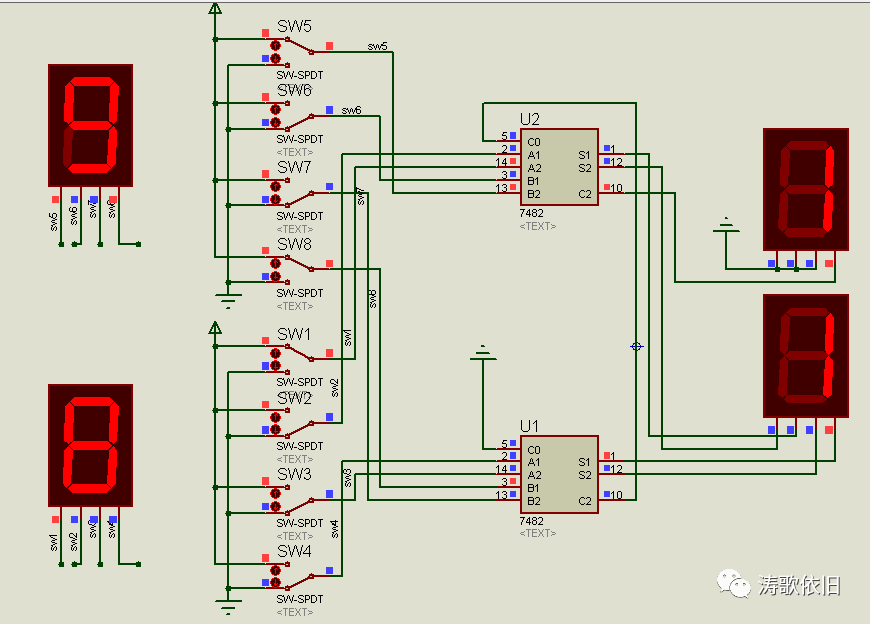
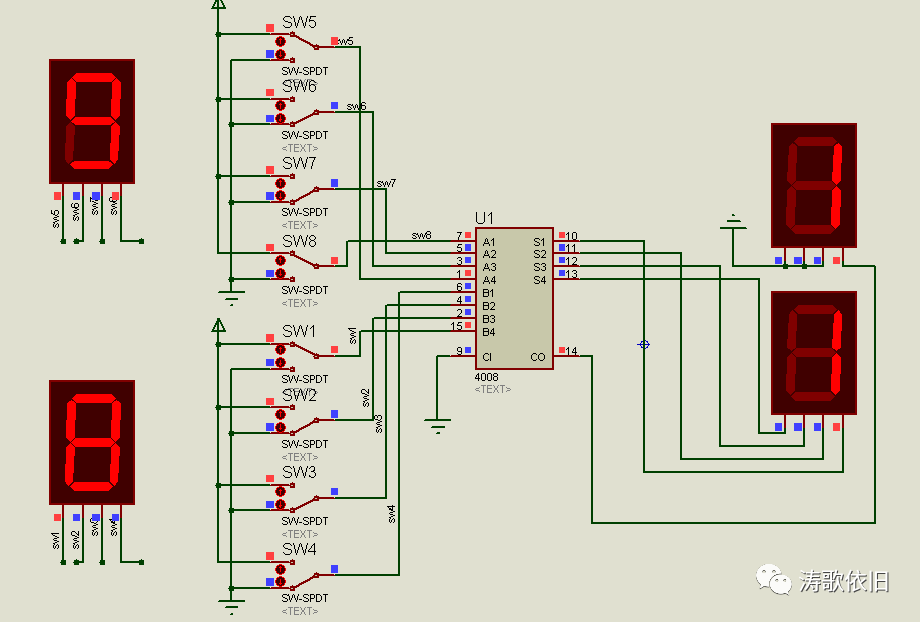
十二. 连续加法器探索
到此为主,我们一步一步地用电路实现了加法。貌似大功告成了,但是,还有个疑问:计算机怎么计算1+2+3+4+5呢?这是个连续加法的问题。我们来尝试用电路图实现,看下图:
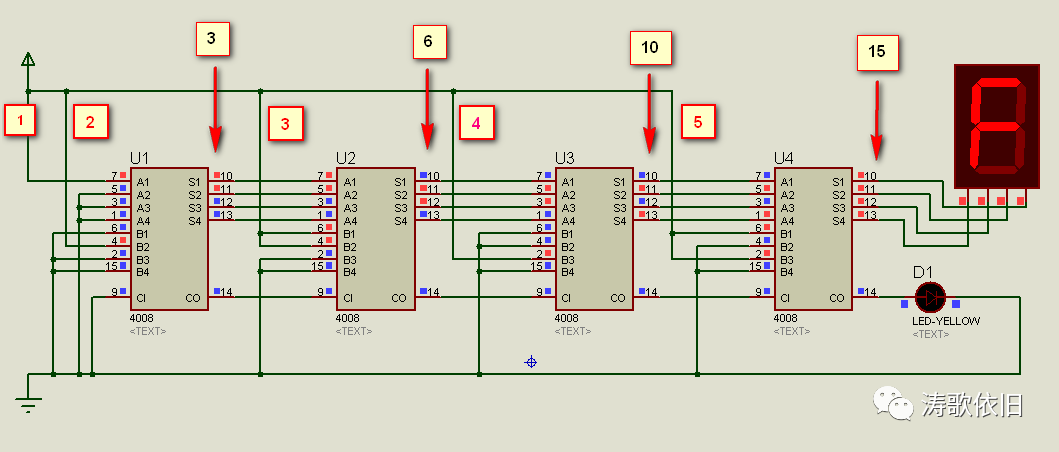
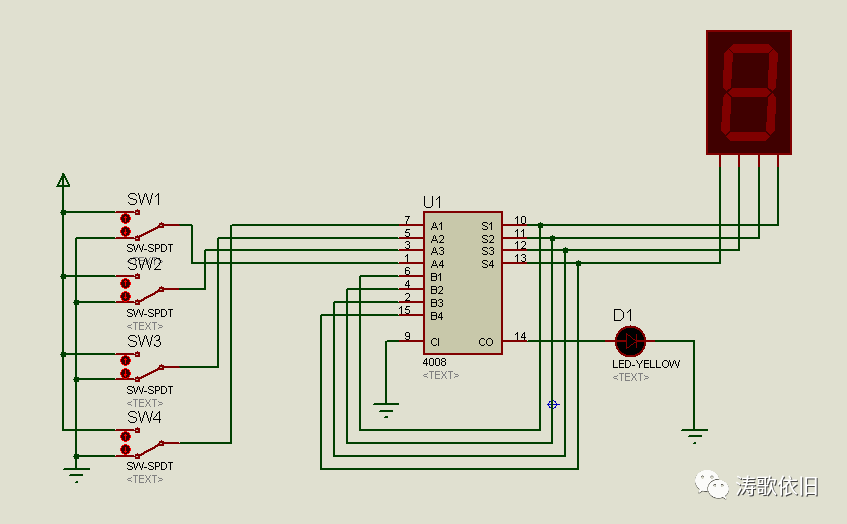
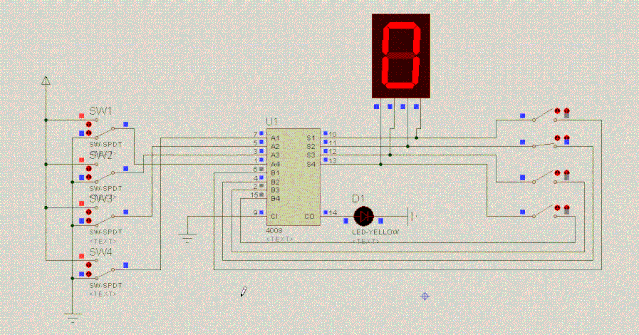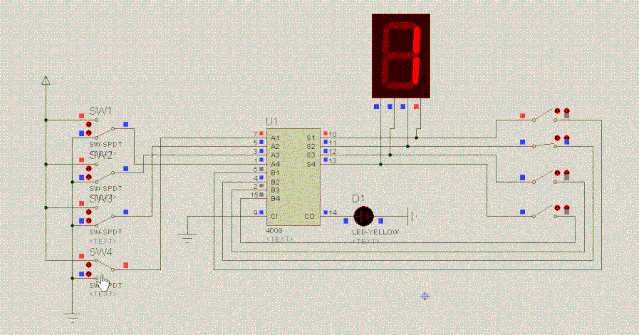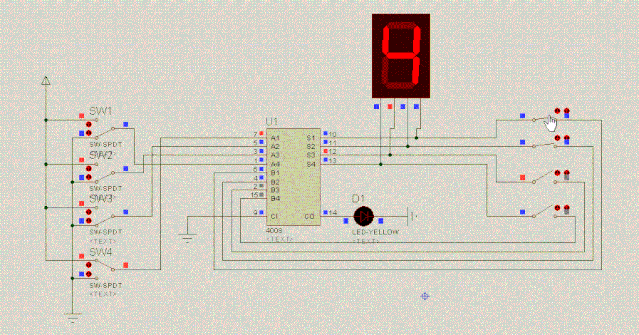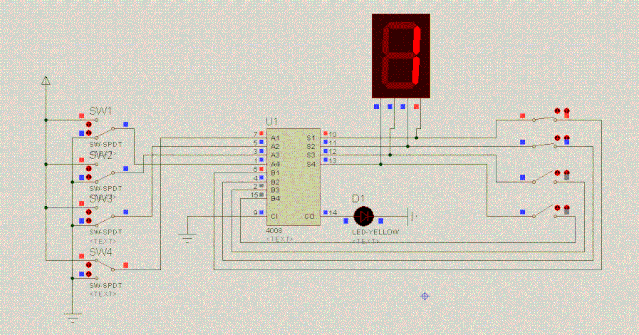
连续加法器的尝试,还是失败了。所谓巧妇难为无米之炊,连续加法器失败的原因在于:它需要特殊的器件,而我们现在还没有接触到这种特殊器件,没办法做连续加法器。
别着急呀。在未来,我们会实现这个连续加法器,而且是全自动的连续加法器,不需要人去掰弄开关。那时,我们顺便体会对电路进行编程的感觉。今天,暂时先聊这么多。
作者/来源:涛哥依旧