简谐振动是怎么跟圆周运动勾搭在一起的？

1. 弹簧振子的简谐振动是个一维问题，而三角函数脱胎于三角学，是个骨子里有着二维“基因”的几何问题，一个一维的东西，怎么会用到二维的表达呢？它们之间是不是有什么几何上的联系呢？

   
   

2. 弹簧振子离开平衡位置的位移应该是个实数，表达式中怎么会出现 虚数 呢 ？
   
   

美丽的欧拉公式

复数与复平面上的点

现在请先让我们关注欧拉公式的等号右边的部分。大家可以看到欧拉公式右边是两项之和，一项是实数 ，另一项是虚数 。 在数学上，我们把这种形如（其中,均为实数）的数称为复数。其中称为该复数的实部，称为复数的虚部，称为虚数单位。

我们都知道，任意实数都可以用实数轴上的一个对应点来表示，那么复数可不可以呢？复数也是可以的。但是呢，复数跟实数不一样。实数只需要一维上的点就可以了，而要想确定一个复数，就得同时确定实部和虚部（即和），所以复数必须由两根数轴构成得一个平面来表示，其中一个数轴用来确定实部的，另一个数轴用来确定虚部的。我们把这样的特殊平面称之为复平面 。

这样，任何一个复数都可以在复平面上找到一个点一一对应，如下图所示。

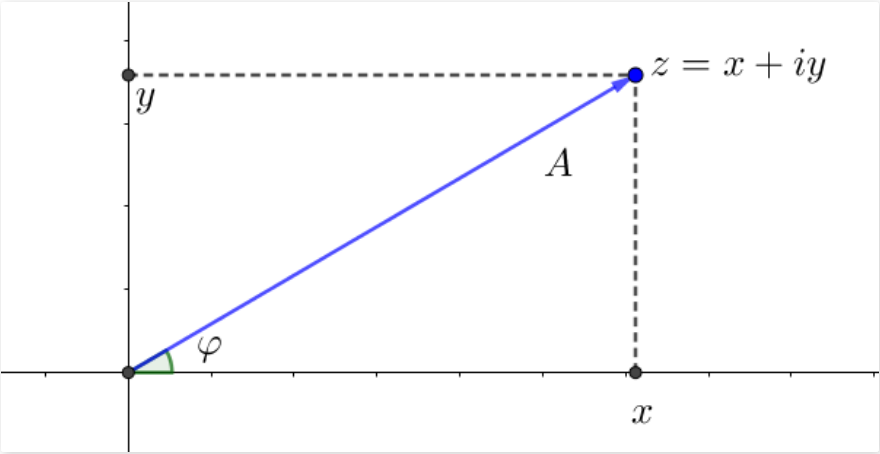
上图其实用了两种坐标来表示复数：一种是用点这种直角坐标形式；一种是用点这种极坐标形式，其中称为复数的模 ，称为复数的幅角。

两种坐标描述同一件事，那么这两种坐标就必须有联系，对吧。大家很容易看出来，两种坐标之间的对应关系可以用下面的两个式子来反映，即

让这个点转圈圈

死点没什么好玩的，让它动起来才有意思。比如我们让这个点匀速转个圈儿。就像下面这样的。

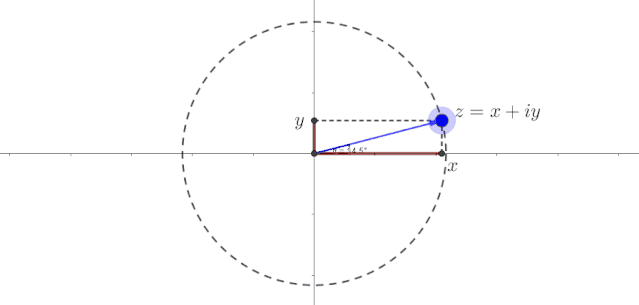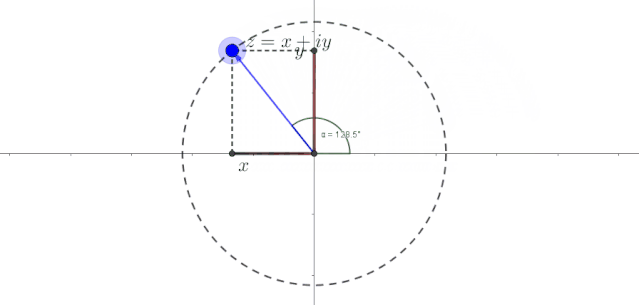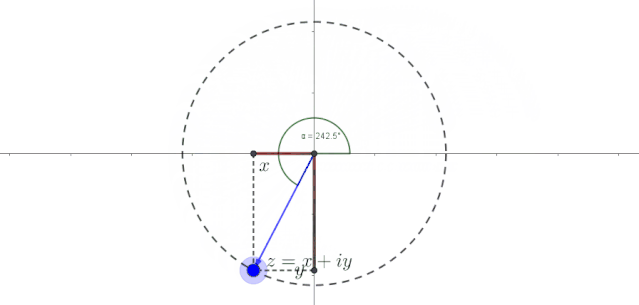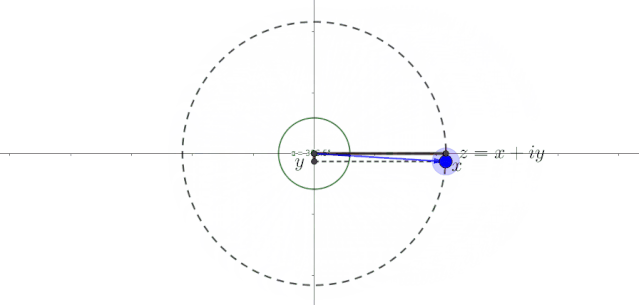
由于标出了点的横轴坐标和纵轴坐标，我们可以直观看到,在点匀速旋转的过程中，和在周期性地变化。它们一会儿取正值，一会儿取负值，一会儿变大，一会变小，而且二者的大小变化是相反的，颇有点儿正弦函数和余弦函数的做派。这可不得了，简谐振动不就是用正弦函数或余弦函数表达的吗？好家伙，是不是隐隐感觉到，匀速圆周运动好像和正余弦函数有那么点儿暧昧的味道。

为了更详细地刻画这个点的匀速圆周运动，我们用极坐标去表达直角坐标。假设在时刻点处在半径为的圆周的一个任意位置上，辐角为，令设点匀速转动的角速度为. 那么在经历了时间之后，点转过的角度值就是。这样的话，点在经历任意时间后的直角坐标位置，就应该是

圆周运动与简谐振动的联系

哈哈，上边这式子不就是简谐振动的表达式吗？为了直观看到匀速圆周运动的横轴和纵轴的变化情况，我制作了下面的这张图片和动图。图片中标示了任意时刻质点的位置坐标在分别横纵轴上的分量，可以看到，随着时间变化，这些分量在按照正余弦函数䣌方式在发生着变化。

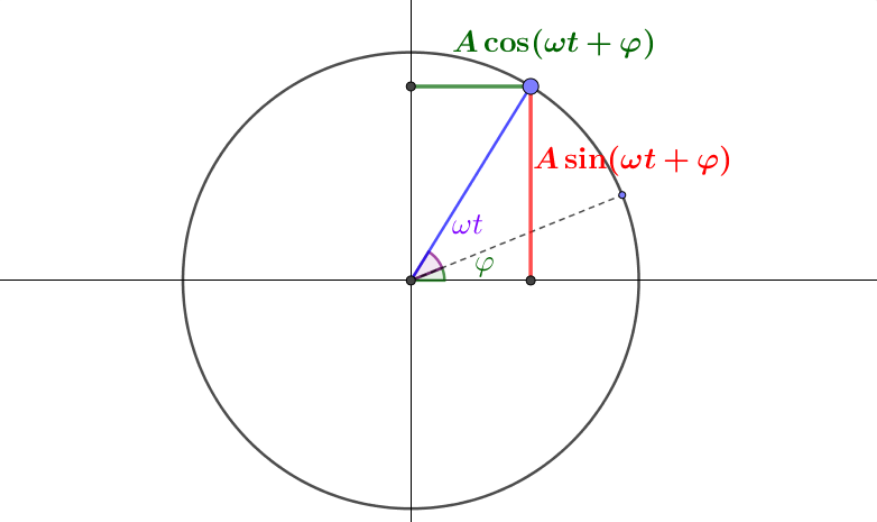
既如此，我们便可以制作一个动图，把匀速圆周运动与简谐振动联系起来了。就像下面这样子：

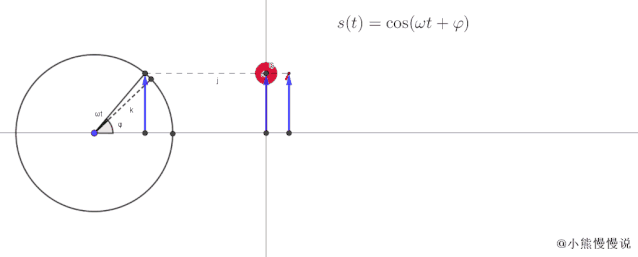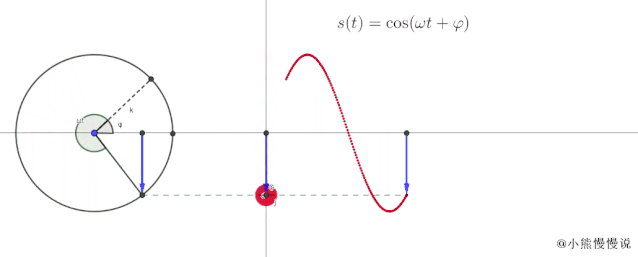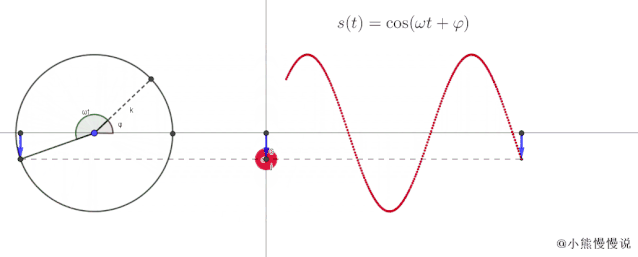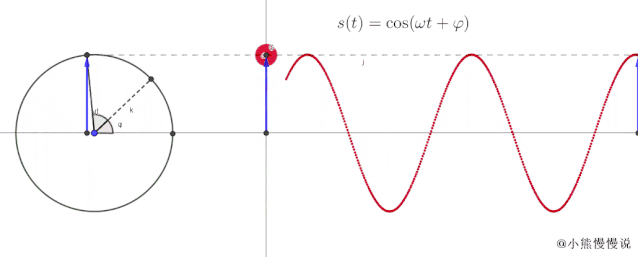
从动中可以看出：

1. 当 点绕半径为的圆周匀速运动时，它的横轴和纵轴随时间的变化情况，和简谐振动是一致的 ；
2. 振动函数中的有了实实在在的直观感觉，就是对应匀速圆周运动在零时刻时的初始辐角，我们称之为初相位，也就是质点的初始位置。而 就是对应匀速圆周运动在初始辐角基础上多旋转的角度 ；
3. 所谓振幅，其实就是对应匀速圆周运动的轨迹半径。

在以前学习简谐振动的时候，由于没有这样的动图辅助理解，导致我们总是搞不清楚相位和初相位是什么意思，以及为什么要取这个名称。现在好了，有了直观认知，对概念的理解就能变得更深一些 。

简谐振动的复指数表示

下面再说说欧拉公式的另一个作用，就是可以用复数来表示简谐振动。我们把欧拉公式中的换成便得到如下形式：

这个式子说明什么呢？它说明，作为复平面上一点的复数，它的实部或虚部可以用来表示一个简谐振动。为什么要这么干呢？因为用指数去讨论一些复杂问题时遇到的计算会比用三角函数来得方便，比如阻尼振动、受迫振动等问题。

最后的话

1. 通过上面的闲聊，我们可以看到，欧拉公式就像一个粘合剂一样，把简谐振动跟圆周运动连接起来了，让我们可以建立不同运动类型之间的联系。而且，欧拉公式也给研究振动问题提供了一个别致的思路，在某些问题中可以用三角函数去分析，而在另一些问题中也许用复指数会更方便一些。

2. 数形结合的方法一直都是理解物理规律和概念的法宝，有时候一句话难以表达的概念，只需要一个给个场景，给个动画，概念的意义就可以轻松被get到，给人一种此时无声胜有声的快感。