π的那些你可能不知道的事实
以下文章来源于大学物理学 ,作者薛德堡
细推物理须行乐,何用浮荣绊此身。

来源:大学物理学
作者:薛德堡
作为一个数,π受到人类的重视,每年的3月14日被称作“圆周率日”,也称π节。后来这一天又被设为“国际数学日”。
关于它的文字一波又一波,但既然它是无限不循环的,它的传奇还在继续,所以它的故事也不能总是那几个,应不断推陈出新才过瘾。
它本名叫阿基米德常数
阿基米德常数是π的别名,不,确切的说,应该是π一开始的名字,因为π这个符号只是牛顿的好朋友William Jones在1706年提出的。那么,为什么它与阿基米德有关?

π最初的出身是作为欧几里德几何中圆与直径的比率被提出的。而作为欧几里德的学生的学生,阿基米德是古希腊——甚至整个人类历史上最伟大的三大数学家之一。第一个记录在案的严格计算π值的算法是使用多边形的几何方法,正是阿基米德在公元前250年左右设计的。
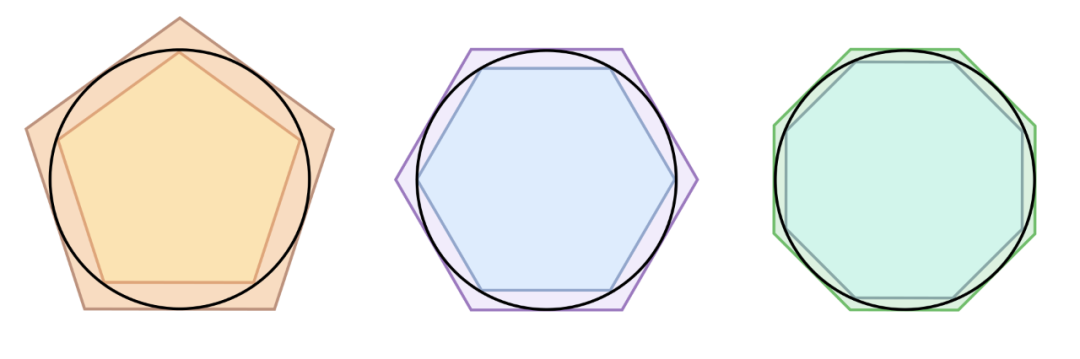
是否可以通过有理数无限接近?
π作为无理数,它是无限不循环的。所以,任何整数构成的分数只能算作它的近似值,而无法代替它。
例如,355/113这个非常接近π的整数比是我国南北朝时的数学家祖冲之发现的,他曾给出了位于3.1415926~3.1415927的高精度圆周率,并保持了800年的不破纪录。
下面是到目前为止发现的一些分数近似值,从左到右依次越来越接近π值。
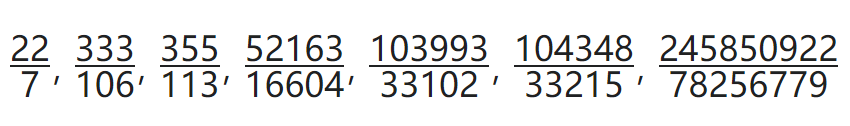
但是,可否通过有理数无限制地接近π值?目前还没有得到结论。
它的数字是完全随机的吗?
π的数字没有明显的模式,这一点已经通过了统计随机性测试,包括正态性测试。当所有可能的数字序列(任意给定长度)出现的频率相等时,无限长的数字称为正常数。π为正态的猜想尚未得到证实。
由于π的数字序列通过了随机性的统计测试,因此它包含一些可能看起来非随机的数字序列,例如从π的十进制表示的第762位开始出现的连续六个数字9的序列。这在数学民间传说中也被称为“费曼点”,以理查德·费曼(Richard Feynman)的名字命名,尽管目前还不知道这与费曼有什么关系。
它是无理数,还是超越数
π不光是无理数,它还是超越数。与
不过,如果放宽限制,可以借助一些特殊的曲线——例如阿基米德螺线来达到目的。
它有很多种定义方式
π有很多种定义,例如最初的就是指欧式几何中圆的周长与直径的比率。它还可被定义为圆与以圆的半径为边的正方形的面积比。这些都是几何定义法。
其实也可以撇开几何,从纯数学的角度来定义π,现代分析之父魏尔斯特拉斯提出如下定义
此外,它还有很多其他的定义方式,来自数论、概率论和统计学等领域。例如Gregory–Leibniz 定理给出的定义是:
计算机怎么快速计算π?
利用某些无穷数列可计算π,例如
后来人们发明了基于计算机的迭代算法,包括Karatsuba算法、Toom–Cook乘法、高斯-勒让德算法等。不过迭代算法通常需要大量的计算机内存。
1914年,印度超级天才数学家拉马努金(Srinivasa Ramanujan)发表了数十个关于π的新公式,这些公式以其优雅、数学深度和快速收敛而著称,其中之一如:
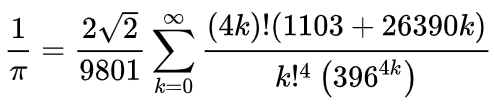
利用该公式,比尔·戈斯珀在1985年创造了π的1700万位数的纪录。
后面,人们还发现了更多π的计算公式。基于这些公式,采取更高效的算法,现在人们已经计算到π的数万亿位了,迄今的最高纪录已经达到62.8万亿位。
这么多位,存储起来都麻烦,如果按照每两个数字一个字节计算,62.8万亿位大概需要30多个T的硬盘!
用模拟的方法得到π值
根据蒙特卡罗方法可获得π。例如巴夫昂投针实验就是这样一种方法:将一根长为 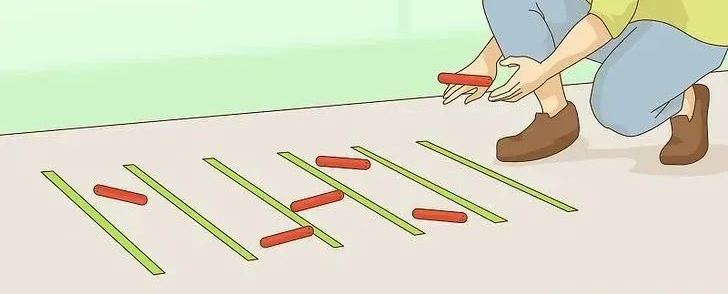
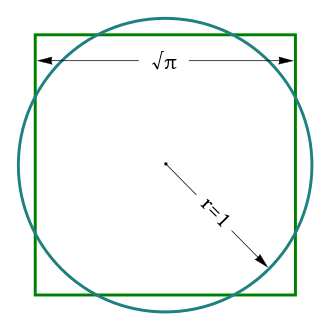
另一种方法是,画一个内接在正方形的圆,然后在正方形上随机撒点。圆圈内的点与点的总数之比大约等于π/4。
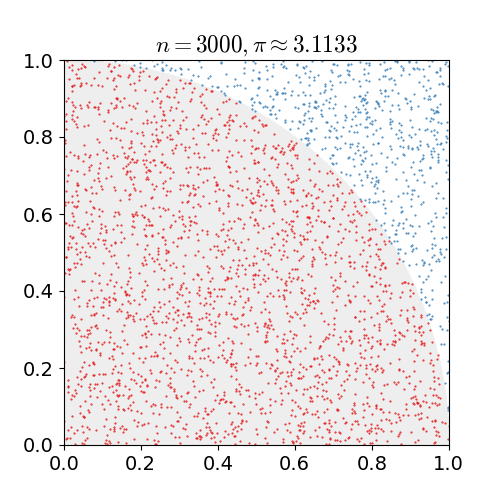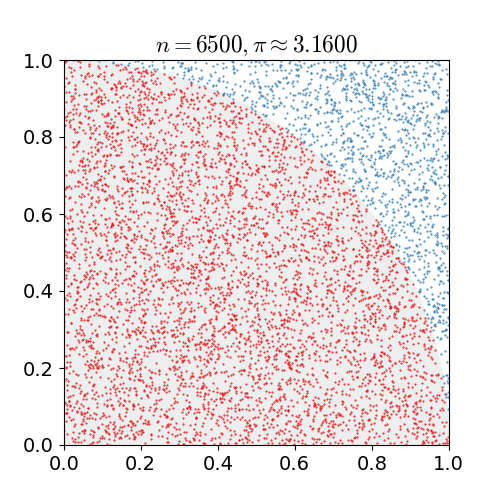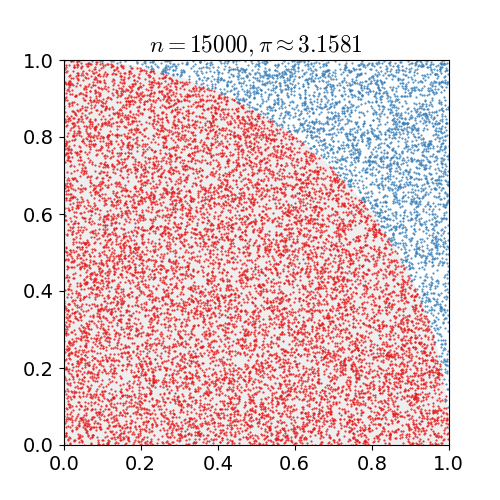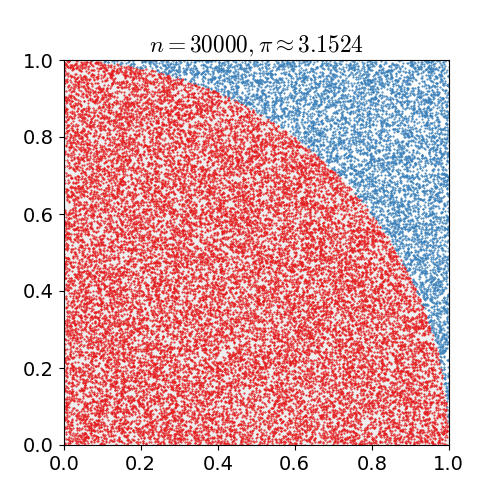
不过,因为计算机只能产生伪随机数,这种模拟的方法对生产随机数有很高的要求,如果随机数不够逼真,得到的结果就会有偏差。
为什么要计算更多π的数字?
以前的人计算圆周率,是要探究圆周率是否是循环小数。但自从1761年兰伯特证明了圆周率是无理数,1882年林德曼证明了圆周率是超越数后,把圆周率的数值算得更加精确,更多都是出于一种好奇。
因为现代科技领域使用的圆周率值,有十几位已经足够了。例如,如果以39位精度的圆周率值来计算可观测宇宙(observable universe)的大小,误差还不到一个原子的体积 。
所以,大多数人获得更长的数字的目的,主要是为了打破已有的纪录。当然,为了测试计算机性能、测试算法以及研究π的数字的随机性,不断获得π值的数字也是有一定意义的。
有什么记忆π数字的方法?
一种常见的技巧是记忆一个故事或诗歌,其中单词长度代表π的数字:第一个单词有3个字母,第二个单词有1个字母,第三个单词有4个字母,第四个单词有1个字母,第五个单词有5个字母,依此类推。
例如“How I wish I could calculate Pi” 这句话中的单词所含的字母的个数依次是3141592。还有人发明这样一个长句用来记π:
How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics.
它代表3.14159265358979。
在其他语言中,人们也创作了用于记忆π的诗歌。例如,中国人都记得一句:“山顶一寺一壶酒”,它代表了3.14159。
2015年3月21日,印度人拉杰维尔·米纳以9小时27分钟的时间背诵了7万位数的π数字,被吉尼斯世界纪录认证。
那些在π日出生或离开的名人
这个日子中出生或者离世的人无数,这里随便记录几个如雷贯耳的人物,他们是:
阿尔伯特·爱因斯坦,1879年3月14日出生。卡尔·马克思,1883年3月14日去世。斯蒂芬·霍金,2018年3月14日去世。

END

编辑:近水楼台
