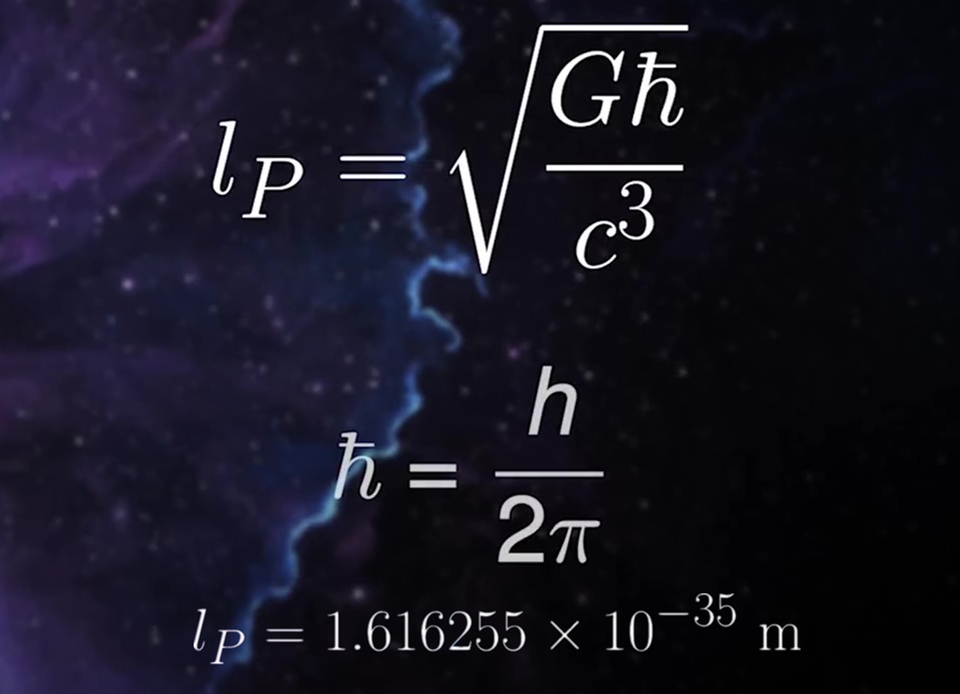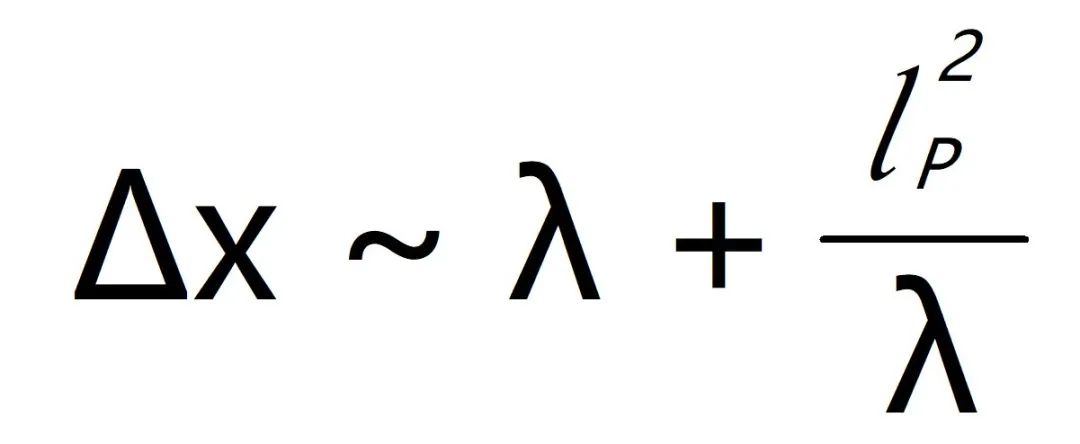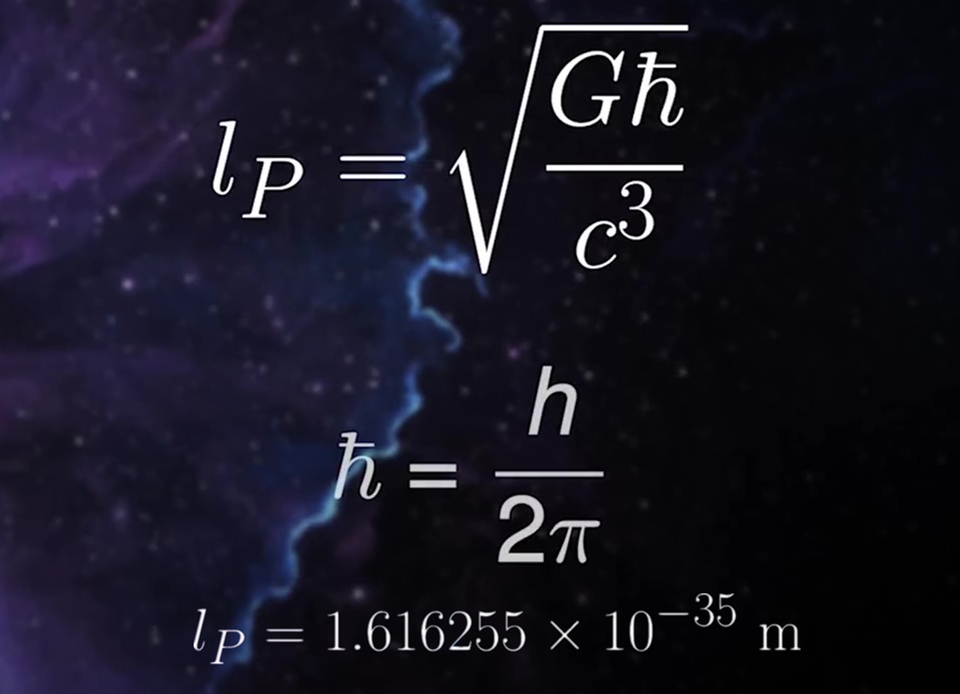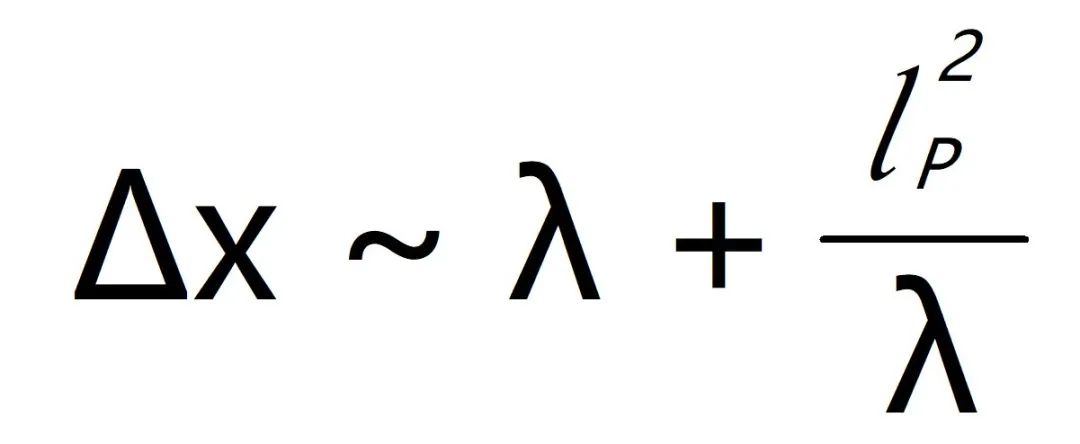以下文章来源于万象经验 ,作者Eugene Wang

19世纪末期,马克思·普朗克通过思考热辐射迎来了量子时代。他发现了对黑体辐射的数学描述不是无限可分的,而是以量子的形式出现。普朗克的发现取决于他的方程式中出现的一个数字——普朗克常数,将光的频率乘以这个常数就可以得到单个光子的能量。我们现在在量子力学中随处可见到它,它是定义量子尺度的自然基本常数。
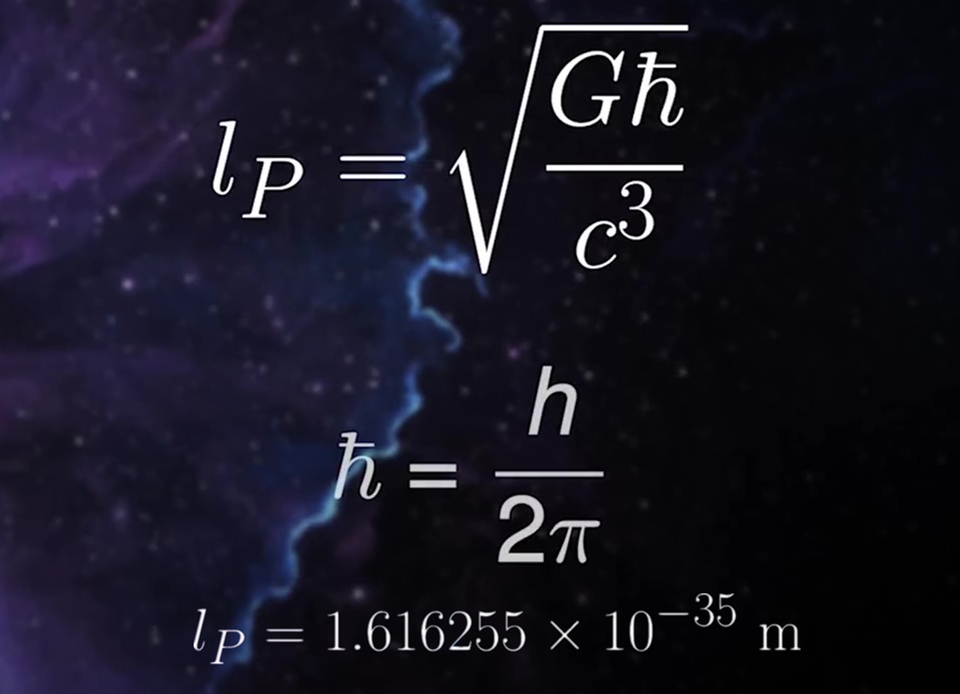
从普朗克常数得出普朗克长度,我们需要以正确的方式结合引力常数、光速和普朗克常数。如您所见,普朗克长度的数值非常小,大约为10^-35米。为什么这种看似随机的常数组成如此重要?因为它代表了空间本身被认为“变成量子”的规模。这里所说的“认为”是因为我们从来没有能够进行如此小规模的实验。所以要理解为什么物理学家认为这个长度如此重要,我们必须在大脑中做一些思想实验。假设我们要测量到某个物体的距离,我们会用一束激光照射它,然后它会把这束激光反射回来。通过此过程所花费的时间,我们就可以推算得到距离了。但是该距离测量具有不确定性,因为我们只能将光返回的时刻记录在电磁波的一个周期内。对于我们使用的任何波长的光,都会产生大约一个波长的距离不确定性。因此,我们只需要使用非常短的波长就可以获得更高的测量精度。
但是,光携带能量和动量。如果我们用强大的短波长X射线激光轰击该物体的话,我们可以得到一个非常精确的距离测量结果,但这会转移很多动量。我们可以尝试降低光束的功率,直到它降到只有一个光子。因为我们不能确切地知道动量转移是如何发生,所以总是会对粒子的最终动量有一个不确定性,这个不确定性大致等于单个光子的动量。光子的动量是普朗克常数除以其波长,因此我们可以将光子的动量替换为被测物体的动量不确定性,并将波长替换为被测物体的位置不确定性,再将其重新排列,我们就可以接近海森堡不确定性公式了。再经过适当的推导,我们就能得到1/4π的因子。这是海森堡自己经历过的推导路线,我们将这种思想实验称为海森堡显微镜。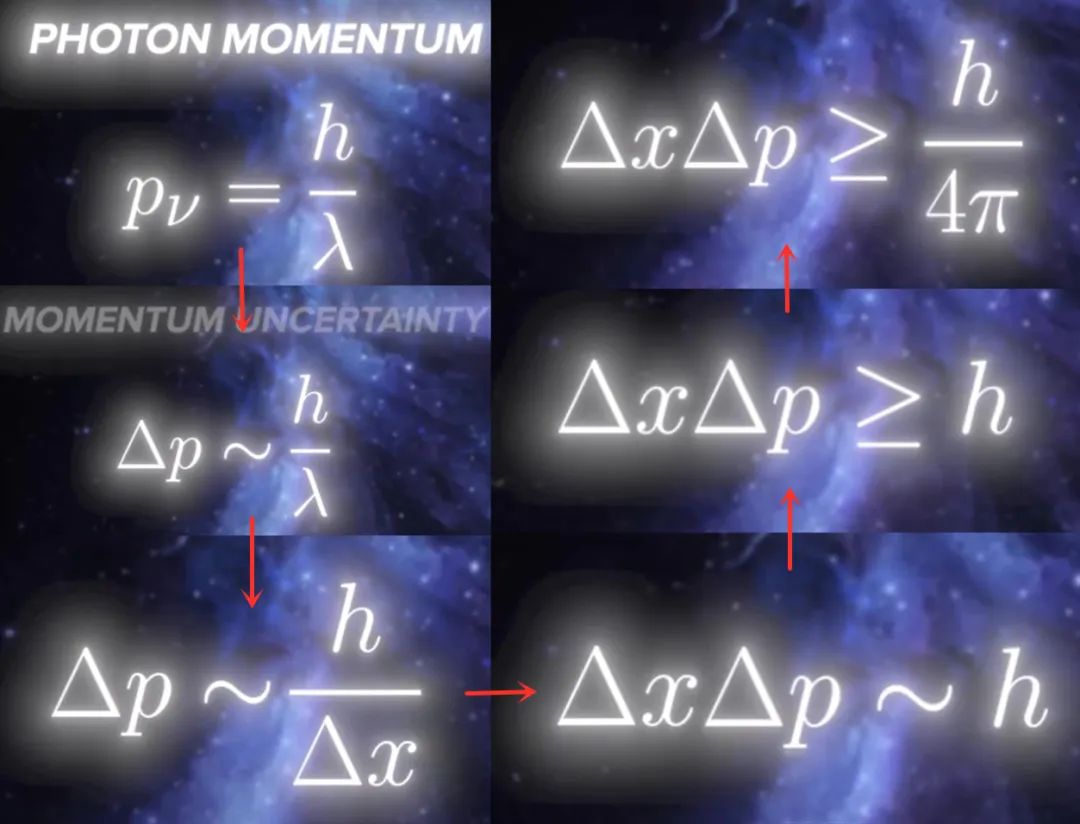
我们现在知道,海森堡不确定性原理不仅仅是测量原理,它也适用于除了位置和动量之外的其他变量对。但我们想重点关注的是,通过不确定性原理公式,我们可以看到普朗克常数代表了我们可以测量的宇宙极限。我们继续这个思想实验,现在添加爱因斯坦的两个关键思想。首先,是质量和能量等价的思想;其次,质量和能量弯曲了时空结构。假设我们正试图以完美地精度测量我们的距离,而不在乎动量。我们不断减少测量光子的波长,这也提高了光子的能量和动量。当我们进一步提高能量时,我们开始注意到一些事情,光子开始产生可观测的引力场。根据著名的爱因斯坦方程,即使光子是无静止质量的,但如果将光子封闭在一个系统中,就会产生我们所谓的有效质量。由此产生的引力场改变了到物体的距离,给距离增加了新的不确定性。让我们深入数学,看看这种不确定性有多大。空间被拉伸的因子等于质量乘以引力常数除以光速的平方。而光子的有效质量是光子的能量除以光速的平方,光子的能量是普朗克常数乘以光速除以波长。整理上面这三个方程,我们可以得到位置的不确定性刚好等于普朗克长度的平方除以波长。
我们可以结合常规海森堡的位置不确定性和空间弯曲的位置不确定性,得到总的位置不确定性。当减少光子的波长时,我们会降低常规海森堡的位置不确定性,但同时也会提高空间弯曲的位置不确定性。不过在一定程度上,总的位置不确定性还是在减少。当光的波长减少到普朗克长度时,这两个不确定性变得相同,并且总的位置不确定性达到最小,这可以从数学上推导出来。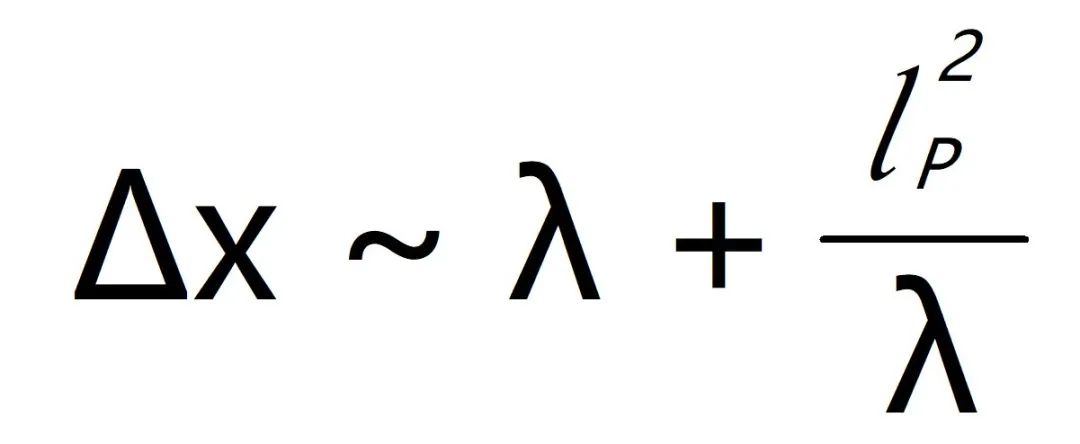
这也就意味着,普朗克长度代表可以测量任何距离的最佳分辨率。它还表示,我们可以有意义地归因于任何事物的最小尺寸。想象一下,我们试图测量一个小于普朗克长度的物体的距离,那么弯曲的时空会改变该尺寸以提供100%的不确定性,因此普朗克长度代表了可测量性的基本极限。那么,这就产生了一个问题,是否意味着不存在更小的尺寸?答案是,我们目前还不知道。
编辑:六块钱的鱼