他被誉为“最后一个什么都知道的人”,其实这句话并不足以描述他,因为他不仅是一个什么都知道的人,他还是一个什么都会的人。
托马斯·杨(Tomas Young,1773-1829),英国物理学家、医生
1792年开始,托马斯·杨学先后在伦敦大学、爱丁堡大学和格丁根大学学习医学,并在23岁取得了医学博士学位。某天,托马斯·杨在看东西时,对眼睛为什么能看清东西产生了疑问。基于对显微镜的了解,以及对牛的眼睛的解剖,托马斯·杨发现了晶状体附近的肌肉结构。进一步的研究发现,该肌肉收缩能改变晶状体的曲率。到了1793年,在托马斯·杨20岁的时候,他在《视力的观察》一文中首次系统且完整地解释了人的眼睛能看到东西的原因。同时,托马斯·杨还解释了散光的原因。
眼睛看东西的原理 | 来源:https://www.sohu.com/a/197467655_208051后来,杨首次提出“三原色原理”,也就是利用光学三原色(RGB):红、绿、蓝(靛蓝)的叠加,可以形成一切色彩的理论。这一原理成为了现代颜色理论的基础。后来,托马斯·杨对光学的痴迷程度继续增加,与医学渐行渐远。光的三原色 | 来源:www.sohu.com/a/399970141_546359
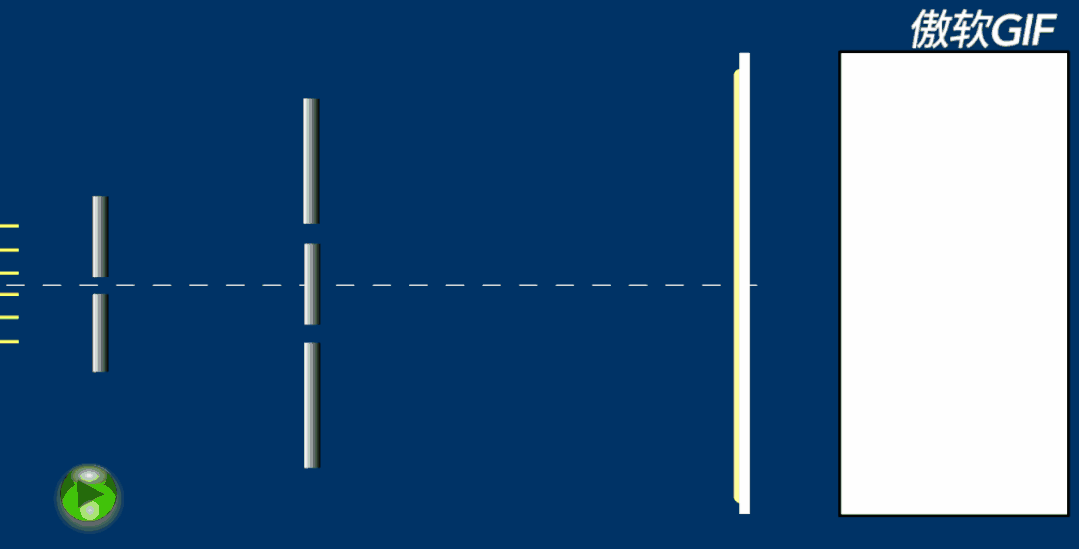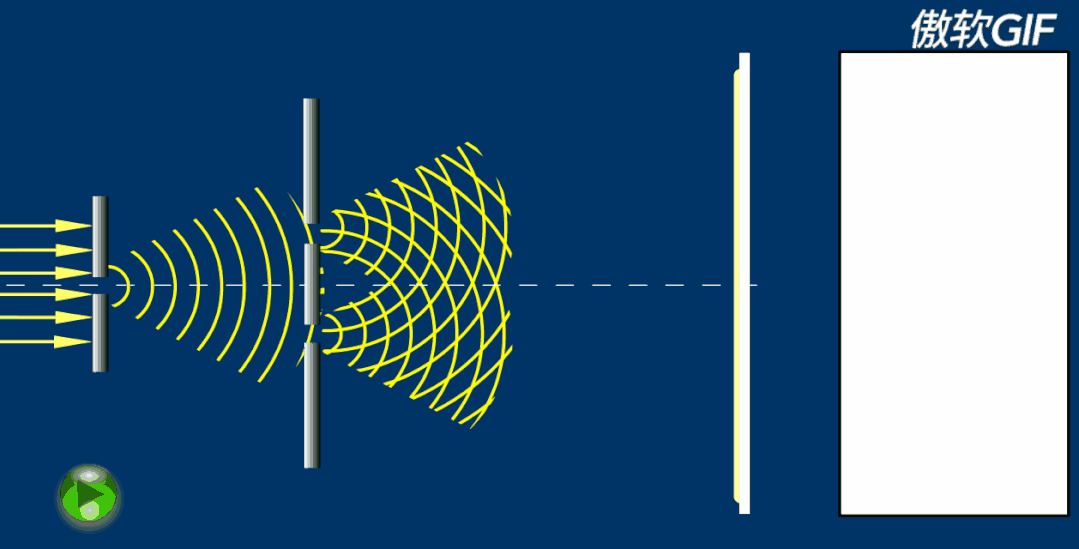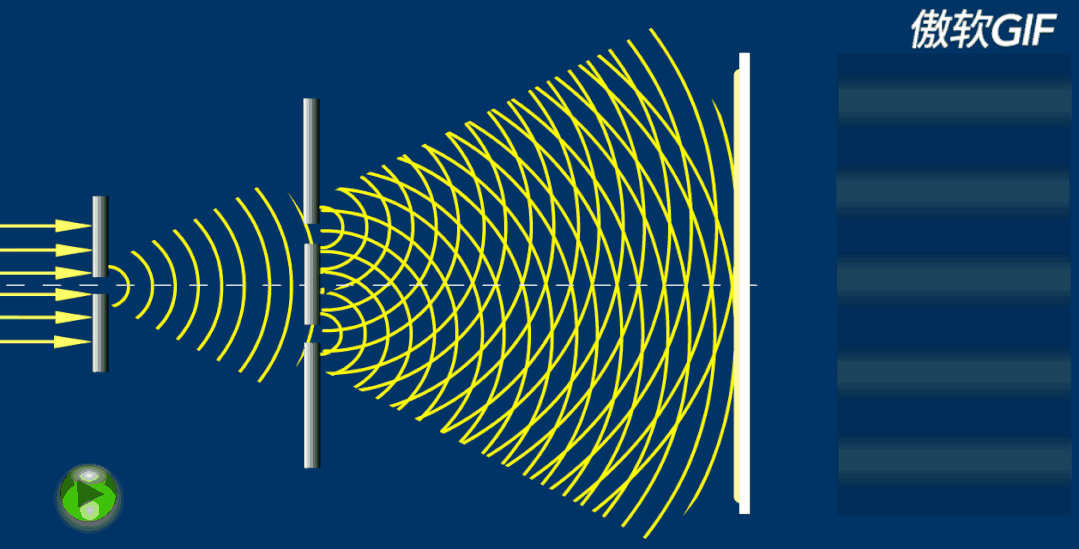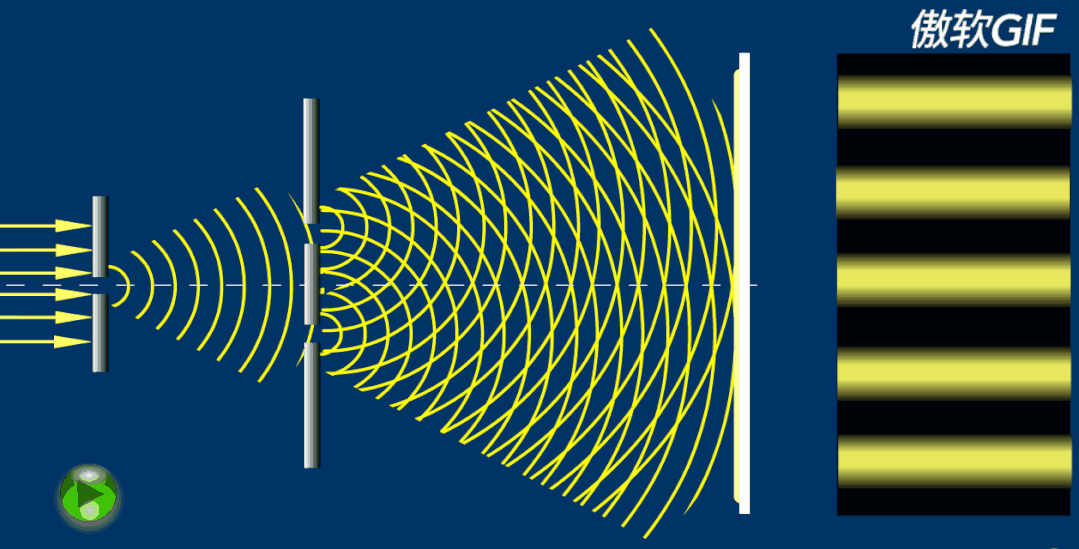
关于光的本质,托马斯·杨与当时的科学权威牛顿爵士产生了分歧。出于对光学、声学的熟悉,使杨坚定地认为“光不是微粒”,也有类似声的波动性。1801年,受水波中干涉现象的启发,托马斯·杨通过著名的杨氏双缝干涉实验,成功演示了光的干涉现象,并在干涉的基础上解释了光的衍射的现象。现在,我们物理书中常用的“半波损失”也是杨提出的概念。托马斯·杨大胆的挑战了牛顿关于光的“微粒说”的结论,也为波动光学的复出奠定了基础,杨也被认为是波动光学的奠基人之一。但是,托马斯·杨的结论在当时仍旧没有被大众接受,这也导致他只能又把精力转移了。https://zhuanlan.zhihu.com/p/145743480?utm_source=com.tencent.mtt
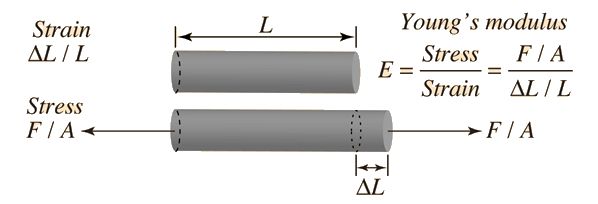
首先说一个词:杨氏模量。没错,这个杨,也是托马斯·杨。这个理论由托马斯·杨在1807年出版的《自然哲学和机械技术讲义》第二卷中提出。对于一个长度为L,截面为S的柱状材料,当其因受力F作用伸长ΔL时,F/S叫应力,其物理意义是金属丝单位截面积所受到的力;ΔL/L叫应变,其物理意义是金属丝单位长度所对应的伸长量。将应力与应变的比就叫弹性模量。这其中,杨氏模量就是一种最常见的弹性模量,其建立在胡克定律基础上。它表征了材料的物理性质,其大小标志了材料的刚性:杨氏模量越大,越不容易发生形变。
其实,早在1805年,托马斯·杨在研究润湿和毛细现象时,就系统描述了界面张力和接触角的定量关系,也就是托马斯·杨方程。但由于多种原因,杨氏方程的力学解释一直存在着争议。直到2020年才被我国学者解释。杨氏模量 | 来源:https://blog.sciencenet.cn/blog-2966991-1007684.html
托马斯·杨13岁时,已经能够阅读拉丁文、希腊语、法语和意大利语。在20岁之前,又将他的语言疆域扩张至东方,开始了对希伯来语、阿拉伯语、波斯语等进行研究。1813年,托马斯·杨投身到罗塞塔石碑的破译工作当中。罗塞塔石碑是拿破仑时期法军在埃及的一个小镇发现了一块古埃及石碑,在石碑上古埃及象形文、古埃及草书,以及古希腊文三种语言记录了同样的一段故事,是解密古埃及文的钥匙。虽然,因为参考材料的问题,托马斯·杨最终没能成功破译,但他的研究成果为法国语言天才商博良(Jean François Champollion,1970-1832)提供了灵感,茅塞顿开的商博良才破解了这种古文字,也为埃及学的研究奠定了基础。虽然商博良坚称这是他自己研究的结果,但有说法,这份荣耀也有托马斯·杨的一份功劳。罗塞塔石碑(现存大英博物馆)| 来源:new.qq.com/rain/a/20210630a04n8z00
光学、力学、数学、医学、天文学、地球物理学、语言学、动物学、考古学、科学史等等,以及声乐和绘画,甚至走钢丝这样的杂技,看起来毫不相关的技艺,但在托马斯·杨的身上却同时上演着。他的足迹涉及到的领域,只有我们想不到,没有他走不到的。虽然托马斯·杨去世时年仅56岁,但他的一生却演绎了一套百科全书。https://new.qq.com/omn/20210723/20210723A0EGD600.html.2021-7-23.[3] Andrew R. Sudden Genius: The Gradual Path to Creative Breakthroughs[M].Oxford university, 2010.https://tech.gmw.cn/2020-04/07/content_33719453.htm.2020-04-07.[5] Robinson A. The story of writing[J]. Story of Writing, 2007.https://www.zhihu.com/question/333447317/answer/1469378533.
编辑:了之