博士Review | 博士创『芯』说第十六期—杨博翰:密码芯片中的随机性基石—硬件TRNG和PUF的设计与思考
 点击上方蓝字关注我们吧!
点击上方蓝字关注我们吧!
4月15日上午,博士创『芯』说第十六期在线上与大家见面。清华大学集成电路学院博士后研究员杨博翰博士受邀作题为“密码芯片中的随机性基石—硬件TRNG和PUF的设计与思考”的报告,与大家一同探讨密码芯片中的关键核心技术。报告由腾讯会议与蔻享学术平台同时直播。临近报告结束,主讲嘉宾与线上的老师同学们针对“真随机数的生成”、“物理不可克隆函数的应用”等问题进行了热烈地讨论。
为丰富学习渠道,扩展学习深度与维度,杨博翰博士应邀为本期报告作文字版详细评述,并于文末附上精彩问答集锦、博士推荐阅读与报告视频回放。让我们通过文字与视频,与杨博翰博士一起重温第十六期的精彩报告吧!
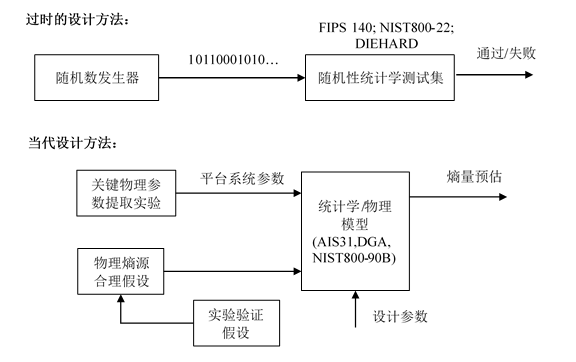
图 1硬件真随机数发生器设计方法的变革
如图1所示,早期真随机数发生器的设计方法强烈依赖于对其输出的统计学检测。但是这些测试集并不能估计真随机数发生器的不可预测性。一个完全没有任何不可预测的伪随机序列、甚至一个无理数的部分序列都是有可能通过这些统计学的测试集的。十多年前开始流行一种新的设计真随机数发生器的方法:首先对物理熵源进行研究;在对熵源的深入理解之上建立其物理模型或者统计学模型;通过实验验证模型中的假设和系统参数;结合设计参数、系统参数和适用的模型,对真随机数发生器能够提供的不可预知性的下界进行估计。当代真随机数发生器[1][2]均有相关的统计学模型支持。
物理不可克隆函数是面向轻量级设备的、用来保存和生成根密钥的低成本的有效解决方案。根据操作机制,硅PUF可以被分为基于延时的PUF和基于存储器的PUF。基于激励-响应对的数量,硅PUF可被分为强PUF和弱PUF。其中,弱PUF [3]只能提供有限数量的 CRP,且该数量和电路尺寸成多项式关系;而强PUF可以提供大量的激励响应对,激励响应对数量和电路尺寸成指数关系,弱PUF被用来生成密钥,而强PUF还被用来作为轻量级的认证。
[1]. Yang, B., Rožic, V.,Grujic, M., Mentens, N., & Verbauwhede, I. (2018). ES-TRNG: AHigh-throughput, Low-area True Random Number Generator based on Edge Sampling. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2018(3),267–292. https://doi.org/10.13154/tches.v2018.i3.267-292
[2]. V. Rozic, B. Yang, W. Dehaene and I. Verbauwhede, "Highly efficient entropy extraction for true random number generators on FPGAs," 2015 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), 2015, pp. 1-6, doi: 10.1145/2744769.2744852.
[3]. K. Chuang, E. Bury, R. Degraeve, B. Kaczer, D.Linten, and I. Verbauwhede, "A Physically Unclonable Function Using SoftOxide Breakdown Featuring 0% Native BER and 51.8fJ/bit in 40nm CMOS," IEEEJournal of Solid-State Circuits 54(10), 12 pages, 2019.
A1:在真随机数发生器的领域,熵指的是在一定的敌手假设下,TRNG能够产生的不可预测性。传统的随机性检测集只是用来分析一个二元序列跟完美均匀分布的之间的差距。一个完全没有任何真随机性(熵等于0)的无限不循环小数的二元序列、或是种子已知的较好的伪随机数发生的输出序列,都能以较大的概率通过这样的随机性检测集。其次这样随机性检测集只能针对有限数量的随机序列的统计学特性,而真随机数发生器的熵描述的是噪声源本身由于其物理随机过程中的不可预测性,在通过熵提取和后处理之后,能够对外输出的不确定性的大小。
Q2:问物理不可克隆函数是否还有非硅的形式?