基于双波长的相位成像和三维形貌测量

来源：先进制造

作者：LAM新媒体

撰稿 | 颜悦（香港中文大学，博士生）

通常物体表面形貌变化多端，对应到光经过该物体透过（或反射）后的波前相位分布也不尽相同。利用双波长技术（DWT, dual wavelength technique）,通过拍频产生的等效合成波长（synthetic wavelength）可以用来反演大范围的波前相位变化，其对应的表面形貌高低范围可从数微米到数厘米。

双波长技术可以适配于相干衍射成像（coherent diffraction imaging, CDI），叠层成像术(Ptychography)，条纹投影轮廓术（fringe projection profilometry , FPP）等等各种光学测量手段。

文章首先介绍了双波长技术的发展历史和基本原理；随后讨论了基于双波长技术的不同应用场景；接着讨论了双波长技术应用于相位成像和三维形貌测量中的测量噪声来源及改进方法；最后对未来双波长技术的发展方向做了展望和总结。

   双波长技术的发展历史和基本原理  

历史发展：

传统单波长干涉或全息方法进行距离测量的主要缺点是测量范围小。因为相位信息只能覆盖 0~2π，对应一个波长范围。一个解决该问题的重要手段就是在光路中加入另外一束不同波长的光，干涉产生拍频从而引入合成波长（可远大于入射光波长）来增大测量范围。双波长技术发展的历史简要如下：

1890s, Michelson 和 Benoit 提出用不同波长干涉来进行绝对相位测量：展示了用四个波长测量了一个1cm的标准具；

1947，Forrester 等人用两束波长非常接近的可见光产生了远大于原可见光的合成波长；

1971，Wyant 首次引入双波长全息方法测量非球面光学元件；

1970s~1980s，激光器的出现和广泛应用之后，基于双波长激光的干涉仪和全息术开始成功应用；

基本原理：

以双波长同轴全息成像（in-line holographic imaging）作为例子。先考虑一束平面波和点光源干涉，其干涉强度可表示为：

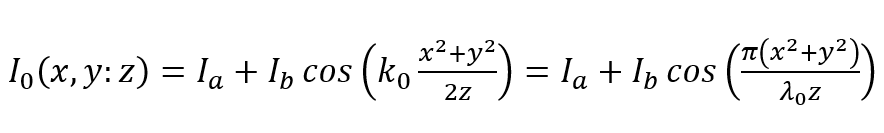
其中 z 为点光源距离测量面的距离，k₀=2π/λ₀，λ₀ 为光波长。

假设两个波长光 λ_1,2 同时使用在光路中，k_1,2=2π/λ_1,2 其干涉条纹的叠加可表示为：

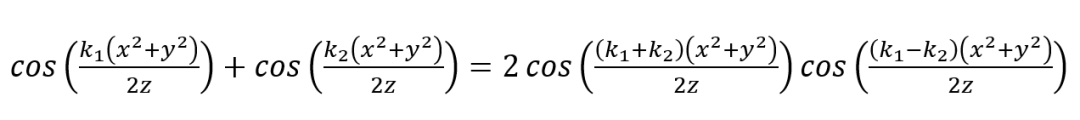
以第二项作为测量信息，可表示为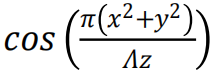：，其中 Λ 就是合成波长：

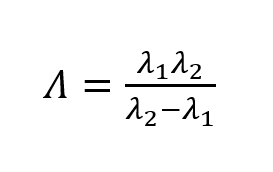
1. 表面形貌测量：测量范围跨度从微米级别到厘米级别

（1）微米尺度物体（指纹特征）

以指纹特征测量为例子，指纹高度特征在数十微米范围。Abeywickrema 等人曾通过使用 514.5 nm 和 457.9 nm 两个激光波长得到合成波长为 4.16 um，对指纹特征进行了精确测量，可以分辨出 1~2 um 的指纹细节，如图1所示。

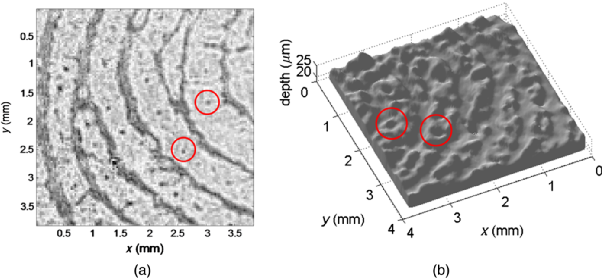
图1：基于双波长干涉的指纹特征测量

（2）厘米尺度

倘若测量对象范围达到厘米级别，则两束入射波长需要非常接近。比如两束中心波长为 632.8 nm 的 He-Ne 激光器，但是其光频率差~为 1GHz，其干涉产生的合成波长~为 30 cm。此外,使用可调谐激光和声光调制器可以更为灵活方便地调整双波长差。需要注意的是，当合成波长很大，两束光波长非常接近，这对实际使用中两束激光器波长稳定要求很高。

2. 基于数字全息的高速成像

在上面介绍的工作中，对于两束不同波长的干涉条纹是分时采集再进行后处理的。为了将双波长技术应用于高通量场景，人们开始研究单次摄像记录的双波长形貌测量。计算机数字全息的发展使得人们可以使用双波长数字全息术实现高速相位成像。一个实际的实现例子如图2所示：

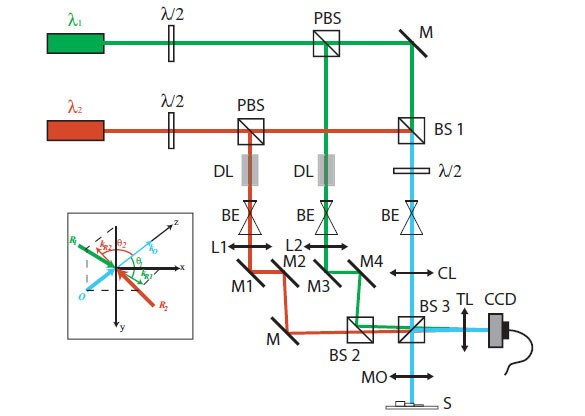
图2：双波长数字全息显微成像光路图

3. 纳米级别分辨率形貌测量

以上介绍的双波长技术测量范围覆盖了微米到厘米级的物体，但却很难分辨纳米级别的形貌特征，因为噪声几乎完全淹没相位图谱。通过条纹细分法（fringesubdivision method）结合双波长技术，可以准确重建出纳米尺度特征。Chen 等人首次实现了该方法，如图 3 所示。两路的相位差为 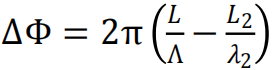，假设测量路 L₂ 产生了微小差异 +Δl₂ ，要使得两路相位差还保持为原来的 ΔΦ，参考路的 L 需要改变的光程差为 +ΔL。得到 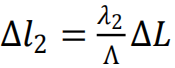，系数 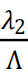 表面条纹分辨率尺度进一步被降低分解，分解的倍数为合成波长 Λ 除以原波长 λ₂。因为合成波长可以设计得很大，因此测量分辨率被大大提高。

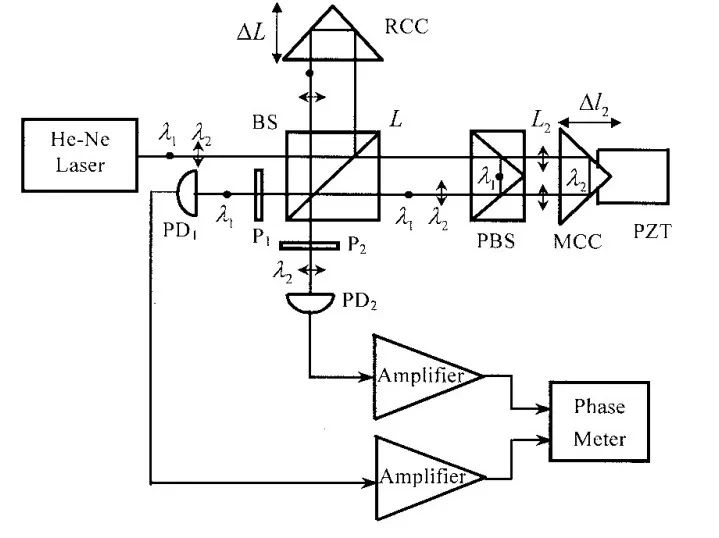
图3：基于条纹细分法的双波长干涉测量

  双波长相位成像和三维形貌检测中的噪声来源  

文章介绍了双波长相位成像检测的噪声来源，总结如下：

(a) 基于系统参数选择的最大可分辨相位限制（Itoh condition）,就是奈奎斯特限制，可表示为：

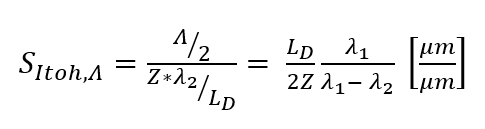
L_D 是探测器尺寸，Z 是探测器距离检测物距离。S_Itoh 越大，表面系统更容易检测到更为陡峭的相位变化（对应物体地形貌高度变化）。

 (b) 根据截断率选择最佳探测器尺寸，截断率是物体尺寸与探测器尺寸的比值T（Truncation 截断条件）。大的T值会导致测量高度的边缘产生波纹。

双波长技术测量可实现大范围测量且避免了相位混叠，且结合条纹细分方法也可实现亚纳米级别的分辨率，其应用已经渗透到各个领域。

未来，双波长可以适配到更多现有光学测量手段中，比如层叠扫描相干衍射成像，非迭代相干成像（基于 Kramers-Kronig 理论）等等。从应用导向角度看，未来双波长技术还可应用于像差矫正，动态波前调控（结合自适应光学理论），光束操控，图像处理等等。

Zhou et al. Light: Advanced Manufacturing (2022)3:17